15. Модели случайных сигналов(нормальный случайный процесс, белый шум, узкополосный случайный сигнал)

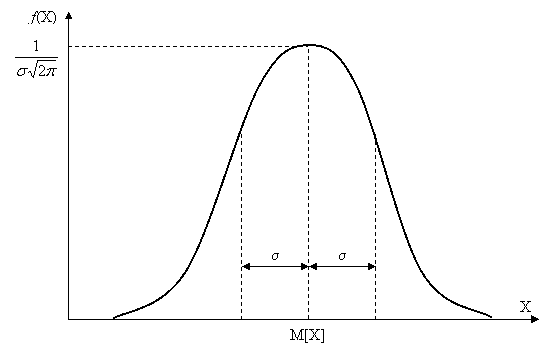
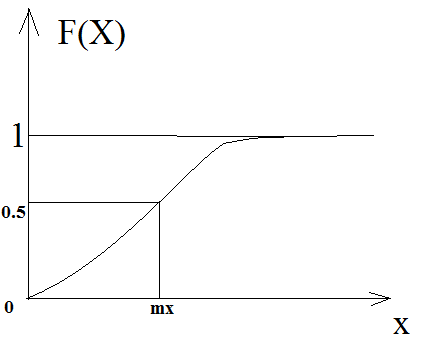
нормальный закон распределения(законом Гаусса)

Случайный процесс x(t) называется гауссовым, если для любого набора фиксированных моментов времени t_n случайные величины x(t_n) подчиняются многомерному нормальному распределению. Плотность вероятностей мгновенных значений x(t) эргодического гауссового процесса определяется выражением:

p(x) = (_x )^-1 exp(-(x-m_x)²/2²). (9.4.17)

Среднее значение и его оценка по достаточно большому интервалу Т:

m_x = x p(x) dx, m_x  (1/T) x(t) dt.

При нулевом среднем (или при центрировании функции x(t) для упрощения расчетов) дисперсия не зависит от переменной t, и равна:

_x² = x² p(x) dx.

Оценка дисперсии при больших значениях Т:

_x²  (1/T) x²(t) dt = S_x(f) df = G_x(f) df. (9.4.18)

Следовательно, плотность вероятностей гауссового процесса полностью характеризуется спектральной плотностью, по которой можно определить значение дисперсии процесса. На вид спектральных плотностей и соответствующих им ковариационных функций никаких ограничений не накладывается.

Белый шум является стационарным случайным процессом q(t), у которого автокорреляционная функция описывается дельта - функцией Дирака и, соответственно, спектральная плотность мощности не зависит от частоты и имеет постоянное значение W_q(f) = ^, равное дисперсии значений q(t). Другими словами, все спектральные составляющие белого шума имеют одинаковую мощность (как белый цвет содержит все цвета видимого спектра). По существу, это идеализированный случайный процесс с бесконечной энергией. Но в случае постоянства спектральной плотности мощности случайного процесса в конечном диапазоне частот введение такой идеализации позволяет разрабатывать достаточно легко реализуемые оптимальные методы фильтрации. Многие помехи в радиотехнике, в технике связи и в других отраслях, в том числе в информатике, рассматривают как белый шум, если эффективная ширина спектра сигналов B_s много меньше эффективной ширины спектра шумов B_q

B_s/B_q << 1,

и спектральная плотность мощности шумов слабо изменяется в интервале спектра сигнала. Понятие "белый шум" определяет только спектральную характеристику случайного процесса, а, следовательно, под это понятие подпадают любые случайные процессы, имеющие равномерный энергетический спектр и различные законы распределения.

Если частотный диапазон спектра, на котором рассматриваются сигналы и помехи, равен 0-В, то спектральная плотность шума задается в виде:

W_q(f)=², 0 f B; W_q(f)=0, f > B, (9.4.7)

при этом корреляционная функция шума определяется выражением:

R_q()= ² Bsin(2B)/2B. (9.4.8)

Эффективный интервал корреляции:

T_k = 2 |R_q()|d /R_q(0). (9.4.9)

Рис. 9.4.4. Функции корреляции белого

шума в частотном интервале 0-В.

Модель белого шума q(t) можно формировать как случайную по времени (аргументу) последовательность дельта - импульсов (t_i) со случайными амплитудными значениями a_i:

q(t) = _i a_i (t-t_i), (9.4.10)

которая удовлетворяет условиям статистической однородности: постоянное среднее число импульсов в единицу времени и статистическая независимость появления каждого импульса от предыдущих. Такой поток импульсов, который называют пуассоновским, является некоррелированным и имеет равномерный спектр плотности мощности:

W_q() = c² = N_a²,

где N - число импульсов на интервале Т реализации случайного процесса, _a² -дисперсия амплитуд импульсов.

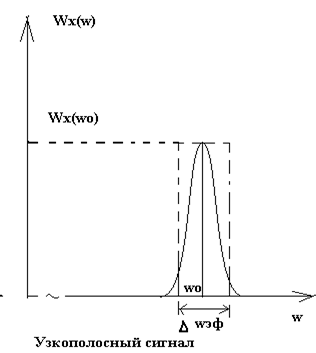Эффективная ширина спектра определяется:

Кореляционная функция