- •1. Назначение автогенераторов и их классификация. Физические явления в автогенераторе.
- •2. Структурная схема автоколебательной системы. Условия баланса фаз и баланса амплитуд.
- •3. Принцип работы lc-автогенератора с трансформаторной обратной связью. Возникновение колебаний и стационарный режим работы.
- •4.Анализ установившегося режима автогенератора. "Мягкий" и "жесткий" режимы самовозбуждения
- •5. Методика определения амплитуды колебаний на выходе lc-генератора в стационарном режиме.
- •6. Вывод дифференциального уравнения автогенератора для случая малых амплитуд и его решение. Недостатки линейного приближения
- •8. Трёхточечные схемы lc-генераторов с емкостной и индуктивной обратной связью.
- •Индуктивная трёхточка Емкостная трёхточка
- •9. Автогенераторы на приборах с отрицательным дифференциальным сопротивлением ( c внутренней обратной связью).
- •12 Законы распределения случайных процессов, их свойства
- •13 Статистические характеристики случайных сигналов, их физический смысл
- •14 Ковариационная и корреляционная функции случайных сигналов, свойства и физический смысл
- •15. Модели случайных сигналов(нормальный случайный процесс, белый шум, узкополосный случайный сигнал)
- •16. Примеры случайных сигналов с различными законами распределения
- •20. Нормальный(гауссовский) з-н распределения случайных сигналов. Эффект нормализации случайных процессов в узкополосных цепях.
- •22. Функция корреляции узкополосного случайного сигнала
- •23. Спектральные характеристики случайных сигналов и их отличие от спектральных характеристик детерминированных сигналов. Теорема Винера-Хинчина.
- •26. Узкополосные случайные сигналы. Необходимость определения статистических характеристик огибающей и фазы этих сигналов.
- •27Законы распределения узкополосного случайного сигнала, его фазы и огибающей.
- •28. Анализ прохождения случайных сигналов через линейные цепи. Постановка задачи.
- •2 K(j ), h(t), g(t) 9. Методика расчета статистических характеристик случайных сигналов на выходе линейного устройства.
- •37.Определение корреляционной функции и спектральной плотности (энергетического спектра) мощности сигнала на выходе.
- •39. Воздействие узкополосого шума на линейный амплитудный детектор.
- •40. Статистические хар-ки шума на выходе квадратичного амп.Дет.
- •34. Воздействие суммы гармонич. Сигнала и узкополосгого случ. Шума.
- •42. Оптимальная фильтрация сигналов в условиях помех. Постановка задачи.
- •43. Передаточная ф-ция согласованного фильтра.
- •44. Импульсная характеристика согласованного фильтра.
- •45. Сигнал и помеха на выходе согласованного фильтра.
- •46. Синтез согласованного фильтра для прямоугольного видеоимпульса и прямоугольного радиоимпульса
- •47. Оптимальная фильтрация сигнала при «небелом» шуме.
12 Законы распределения случайных процессов, их свойства
13 Статистические характеристики случайных сигналов, их физический смысл
14 Ковариационная и корреляционная функции случайных сигналов, свойства и физический смысл
Закон распределения – закон, устанавливающий связь между возможными значениями случайной величины и соответствующими вероятностями. Непрерывная СВ имеет бесчисленное мнжество возможных значений. На практике используются наиболее общие формы закона распределения, получ названя интегральный и дифференциальный з-н распределения вероятностей.
Одномерные законы распределения(хар-ет 1 СВ) Пусть X – случайная величина, x – некоторое текущее ее значение. Для количественной характеристики распределения случайной величины X принимается функция
F ( x ) = P( X ≤ x ) ,(1)
где P ( X ≤ x ) – вероятность того, что случайная величина X не превосходит значения x.
Функция F (x ) является по существу законом распределения случайной величины X, который называется интегральным законом распределения или функцией распределения. Она обладает следующими свойствами, вытекающими из равенства (1):
1. F (−∞ ) = 0; F (∞ ) = 1 .
2. F ( x2 ) ≥ F ( x1 ) при x2 > x1 .
3. P( x1 < X ≤ x 2 ) = F ( x 2 ) − F ( x1 ) .
Функция распределения F (x ) в общем случае является неубывающей функцией, значения которой находятся в пределах от 0 до 1
Для
дискретной СВ
![]()
где σ ( x − x k ) – единичная функция (функция Хевисайда), равная 1 при x ≥ xk ; 0 при x < xk .
Дифференциальный з-н распределения(плотность распределения)
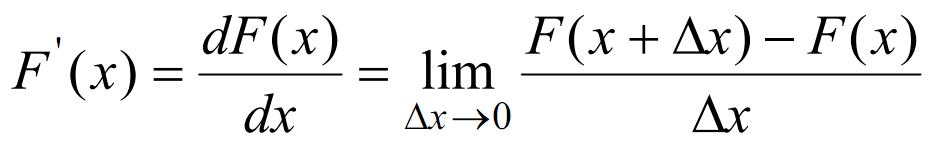
Р(х)=
В числителе указана вер-сть попадания в итервал дельта х в знаменателе величина интервала, отсюда вознивает понятие плотность и размерность1/В
P(x)dx=dF(x)- вероятность того что число х в бесконечно малом интервале dx имеет некотрое значение
Свойства.1)p ( x ) > 0 2) ∫ p( x )dx = 1 (интеграл от –∞ до +∞) 3)∫ p( x )dx = F ( x ) (интеграл от –∞ до х)
Для дискретной СВ
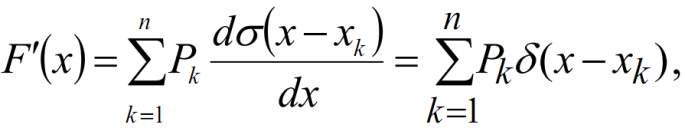
Р(х)=
где δ ( x − x k ) – дельта-функция (функция Дирака), равная ∞ при x = x k, 0 при x ≠ x k
В общем случае, наиболее полной характеристикой случайного процесса является n-мерная плотность вероятности p n ( x1 , x 2 ,..., x n ; t1 , t 2 ,..., t n ) при достаточно большом n, которая характеризует совместное вероятностное распределение случайных величин X 1 = x(t1 ), X 2 = x(t 2 ), ..., X n = x(t n ) . Оперировать с таким законом распределения практически невозможно. Поэтому при исследовании случайных процессов рассматривают, как правило, одномерную p( x, t ) и двумерную p2 ( x1 , x 2 ; t1 , t 2 ) плотности вероятности.интегральный закон распределения(функция распределения вероятностей)
При решении практических задач иногда нет необходимости знать законы распределения случайных величин и процессов, а достаточно иметь только отдельные их числовые характеристики, которые в сжатой форме отражают существенные особенности распределения. Кроме того, с помощью числовых характеристик и операций с ними удается в ряде случаев решать широкий круг задач статистической радиотехники до конца без использования законов распределения. Наибольшее применение нашли такие числовые характеристики,как математическое ожидание, дисперсия и корреляционная функция.
Математическое ожидание – это начальный момент первого порядка, характеризующий среднее значение случайной величины или случайного процесса.
Дисперсия – это центральный момент второго порядка, который характеризует среднюю величину возможных отклонений (т.е. возможный разброс) значений случайной величины или случайного процесса относительно математического ожидания.
Корреляционная функция характеризует степень статистической связи значений случайного процесса в различные моменты времени.
Для ДСВ
![]()

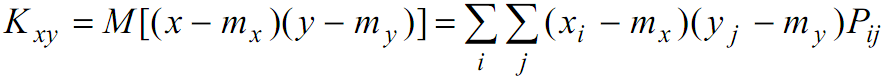
Для НСВ
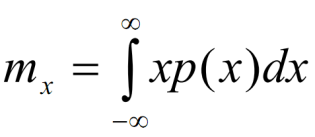


Нестационарный случайный процесс
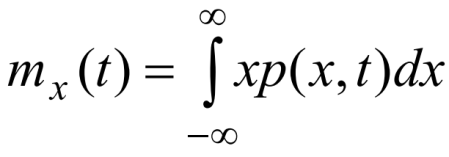

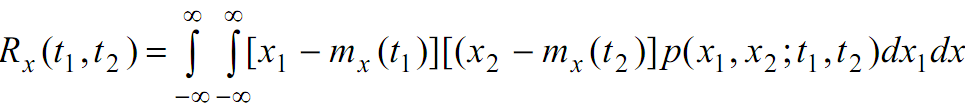
Стационарный случайный процесс