44. Импульсная характеристика согласованного фильтра.

Рассмотрим импульсную характеристику h(t) согласованного фильтра. Учитывая, что g(t) любого фильтра связано c K(j) преобразованием Фурье, находим:

Импульсная характеристика:

.

Учитывая, что и вводя новою переменную , получим:

.

Т. е. если задан сигнал s(t), то импульсная характеристика определяется как:

.

Построение графика функции s(t₀––t): кривая s(-t) является зеркальным отражением заданного сигнала s(t). Функция же s(t₀—t) сдвинута относительно s(-t) на величину t₀ вправо, также зеркальна по отношению к исходному сигналу s(t), с осью симметрии проходящей через точку t₀/2.

Так как импульсная характеристика не может быть отрицательной, то t₀ не может быть меньше , чем Т_с (длительность сигнала).

При увеличении t₀ возрастание сигнала не будет, а будет наблюдаться сдвиг сигнала вправо. Условие t₀Т_с накладывает на сигнал требование его конечной длительности.

Вывод: Применение согласованной фильтрации возможно при импульсном сигнале или ограниченной по времени пачке импульсов.

45. Сигнал и помеха на выходе согласованного фильтра.

Используем соотношение: . Подставив в него получим:

Т. е. выходной сигнал будет повторять форму корреляционную функцию смещенную во времени.

При t=t₀ R_вх=Э и выражение переходит в .

Рассмотри параметры шума. Наиболее распространен белый шум – нормальный шум со спектральной плотностью W₀=const. При действии нормального шума на линейную цепь на выходе шум остается нормальным и . Следовательно корреляционная функция шума на выходе:

Следовательно, корреляционная функция на выходе по форме совпадает с автокорреляционной функцией входного сигнала и с входным сигналом.

При =0 найдем дисперсию шума на выходе:

Найдем соотношение сигнал/шум на выходе согласованного фильтра (определим не по мощности а по напряжению: .

46. Синтез согласованного фильтра для прямоугольного видеоимпульса и прямоугольного радиоимпульса

Зададим сигнал как

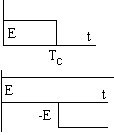
Спектральная плотность такого сигнала: .

А его модуль: .Используя оотношение найдем передаточную функцию согласованного фильтра: . Импульсная характеристика фильтра совпадает по форме с самим сигналом: .

Необходимо отметить, что сходящийся, т. е. фильтр физически реализуем.

Структурная схема имеет следующий вид. Множитель 1/j реализуется интегрирующим звеном, а множитель реализуется устройством вычитания сигнала без задержки и с задержкой Т_С. Реализация такого устройства в идеале невозможно, но можно получить хорошее приближение при использовании реальной интегрирующей RC-цепи, если обеспечить постоянную времени этой цепи, достаточно большую по сравнению с Т_с.

Получающийся при этом на выходе вычитающего устройства импульс может быть сделан достаточно близким к прямоугольному.

Спектр радиоимпульса представляется ф-лой:

В рассматр. случае

В результате прохождения фильтра получим: