42. Оптимальная фильтрация сигналов в условиях помех. Постановка задачи.

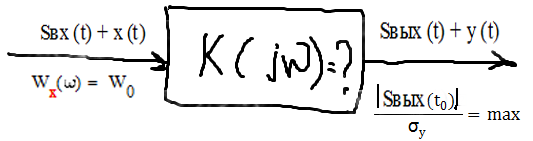
1. на вход поступает аддитивная смесь сигнала и шума Sвх(t) + x(t)

2. Шум белый W_x (w) = W₀

3. Задача решается в рамках линейной фильтрации Sвых(t) + y(t), т.е. Sвых(t) = f (Sвх(t))

y(t) = f ( x(t) )

4. Определить частотный коэффициент передачи лин. фильтра K ( jw ), который обеспечивает max отношение вых. сигнала в какой-то момент времени t₀ к среднеквадратическому значению шума на выходе

Для определения K ( jw) необходимо получить выражение и найти его максимум. Получим это выражение:

1. Получение

а) б)

в) берем обратное преобраз. Фурье :

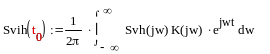
2) Получение

а)

б)

В)

Г) = Т.о. можно записать:

=

Для определения K ( jw), обеспечивающего максимум данного выражения, воспользуемся нер-вом Коши-Буняковского:

Левая часть будет max в случае равенства, а рав-во соблюдается при условии:

f₂(x) = A f₁* (x) , где А – произвольное число

f₁(x)  Sвх (jw) exp ( jwt₀ )

f₂ (x)  K ( jw )

Предположим, что условие f₂(x) = A f₁* (x) соблюдается, тогда можно записать:

=

=

= Э равенство Персиваля

= ,

запишем св-ва с учетом обозначений:

Перепишем получ. рав-во в след.виде :

Это равенство позволяет записать след:

1. K (w) = A Sвх (w) – АЧХ

2. фи (w) = - ( фи_s(w) + wt₀ )

Вывод : АЧХ фильтра с точностью до постоянного множителя равна амплитудному спектру вх. сигнала. Название такого фильтра – согласованный. Соглас. фильтр – фильтр, АЧХ которого согласована с амплитудным спектром вх. сигнала. ФЧХ фильтра равна фазовой хар-ке сигнала, взятого с обратным знаком.

43. Передаточная ф-ция согласованного фильтра.

В отношении спектральных плотностей с/п= |y (t₀) |/ s_{n вых} числитель должен быть максимальным в заданный момент времени, поэтому необходимо рассматривать фазовый спектр. Так как спектр представлен в виде косинусных колебаний, они должны суммироваться на выходе цепи в фазе, чтобы максимальное мгновенное значение было при t = t₀, т.е. j_к (w) = -j_s (w) - wt₀ - такие требования к фазовой характеристике обеспечат заданные требования по максимизации y (t₀). Модуль передаточной функции цепи должен с точностью до постоянного множителя повторять модуль спектральной плотность сигнала K (w) = AS (w). С учетом требований к фазовой характеристике цепи K (jw) = AS (w) exp [-jj_s (w)] exp (-jwt₀), так как S (jw) = S (w) exp [jj_s (w)], то K (jw) = AS (jw) exp (-jwt₀).

Покажем, что найденное выражение для комплексного коэффициента передачи является оптимальным в смысле максимума отношения с/п = |y (t₀) |/s_{n вых}. Для линейной цепи справедлив принцип суперпозиции, т.е. можно отдельно рассматривать прохождение сигнала и шума:

|y (t₀) | = | (2p) ^-1/2 S (jw) K (jw) exp (-jwt₀) dw|,

а s_{n вых} = [ (2p) ^-1/2 W_n (w) K² (w) dw] ^1/2.

Подставим полученные выражения в отношение сигнал/помеха:

|y (t₀) |/s_{n вых} = | (2p) ^-1/2 S (jw) K (jw) exp (-jwt₀) dw|/ [ (2p) ^-1/2 W_n (w) K² (w) dw] ^1/2.

В математике существует неравенство Шварца:

| F₁ (x) F₂ (x) dx|² £ [ |F₁ (x) |²dx] [ |F₂ (x) |²dx],

где F₁ (x) и F₂ (x) - некоторые комплексные функции. Применим это неравенство для нашего случая. Тогда отношение сигнал/помеха с/п £ 1/ [ (2p) ^-1 S² (w) dw] ^1/2. Так как Э_s = (2p) ^-1 S² (w) dw, то с/п £ 1/ . При этом значении с/п K (jw) = K_опт (jw). Это неравенство превращается в равенство при условии, что F₂ (x) = F₁ (x). Применим это условие к K (jw), получим K_опт (jw) exp (jwt₀) = AS (jw), тогда K_опт (jw) = AS (jw) exp (-jwt₀).

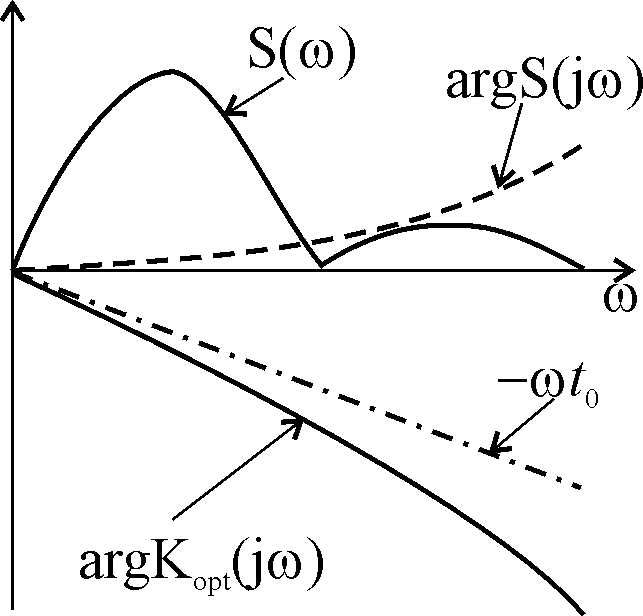
Отсюда следует, что интуитивные рассуждения, которые привели к такому же выводу, верны, а exp (-jwt₀) определяет запаздывание максимального значения выходного сигнала на t₀. Амплитудно-частотная характеристика K_опт (w) = AS (w), фазочастотная характеристика j_опт (w) = -j_s (w) -wt₀.