- •1. Назначение автогенераторов и их классификация. Физические явления в автогенераторе.
- •2. Структурная схема автоколебательной системы. Условия баланса фаз и баланса амплитуд.
- •3. Принцип работы lc-автогенератора с трансформаторной обратной связью. Возникновение колебаний и стационарный режим работы.
- •4.Анализ установившегося режима автогенератора. "Мягкий" и "жесткий" режимы самовозбуждения
- •5. Методика определения амплитуды колебаний на выходе lc-генератора в стационарном режиме.
- •6. Вывод дифференциального уравнения автогенератора для случая малых амплитуд и его решение. Недостатки линейного приближения
- •8. Трёхточечные схемы lc-генераторов с емкостной и индуктивной обратной связью.
- •Индуктивная трёхточка Емкостная трёхточка
- •9. Автогенераторы на приборах с отрицательным дифференциальным сопротивлением ( c внутренней обратной связью).
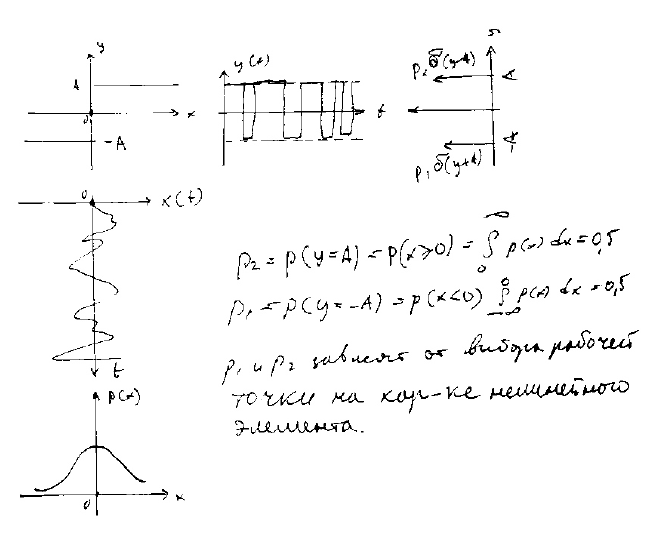
- •12 Законы распределения случайных процессов, их свойства
- •13 Статистические характеристики случайных сигналов, их физический смысл
- •14 Ковариационная и корреляционная функции случайных сигналов, свойства и физический смысл
- •15. Модели случайных сигналов(нормальный случайный процесс, белый шум, узкополосный случайный сигнал)
- •16. Примеры случайных сигналов с различными законами распределения
- •20. Нормальный(гауссовский) з-н распределения случайных сигналов. Эффект нормализации случайных процессов в узкополосных цепях.
- •22. Функция корреляции узкополосного случайного сигнала
- •23. Спектральные характеристики случайных сигналов и их отличие от спектральных характеристик детерминированных сигналов. Теорема Винера-Хинчина.
- •26. Узкополосные случайные сигналы. Необходимость определения статистических характеристик огибающей и фазы этих сигналов.
- •27Законы распределения узкополосного случайного сигнала, его фазы и огибающей.
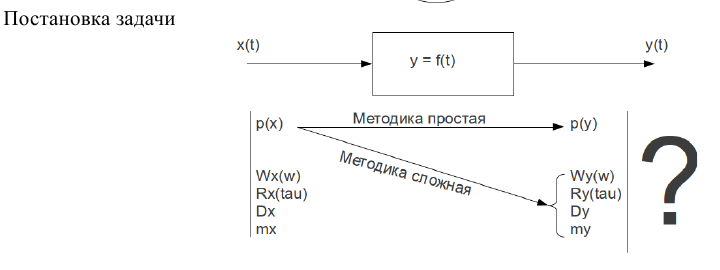
- •28. Анализ прохождения случайных сигналов через линейные цепи. Постановка задачи.
- •2 K(j ), h(t), g(t) 9. Методика расчета статистических характеристик случайных сигналов на выходе линейного устройства.
- •37.Определение корреляционной функции и спектральной плотности (энергетического спектра) мощности сигнала на выходе.
- •39. Воздействие узкополосого шума на линейный амплитудный детектор.
- •40. Статистические хар-ки шума на выходе квадратичного амп.Дет.
- •34. Воздействие суммы гармонич. Сигнала и узкополосгого случ. Шума.
- •42. Оптимальная фильтрация сигналов в условиях помех. Постановка задачи.
- •43. Передаточная ф-ция согласованного фильтра.
- •44. Импульсная характеристика согласованного фильтра.
- •45. Сигнал и помеха на выходе согласованного фильтра.
- •46. Синтез согласованного фильтра для прямоугольного видеоимпульса и прямоугольного радиоимпульса
- •47. Оптимальная фильтрация сигнала при «небелом» шуме.
2 K(j ), h(t), g(t) 9. Методика расчета статистических характеристик случайных сигналов на выходе линейного устройства.
X(t) Y(t)
(закон распределения)
(спектральная плотность мощности)
(корреляционная функция)
(дисперсия)
(мат. ожидание)
передаточная функциия K(j )(частотный коэффициент передачи)
импульсная характеристика h(t)
переходная характеристика g(t)
В общем виде задача изучения прохождения случайных сигналов через линейные цепи состоит в определении закона распределения (функции распределения или плотности вероятности) процесса на выходе цепи при известных законе распределения входного случайного процесса и характеристик цепи. Как правило, решение задачи в общем виде наталкивается на существенные трудности. Поэтому, обычно указанную задачу сводят к определению вероятностных характеристик (математического ожидания, дисперсии, автокорреляционной функции) выходного случайного процесса. Объясняется это тем, что для практики построения и анализа радиотехнических устройств вполне достаточно знания этих характеристик.
Наиболее эффективным методом решения задачи прохождения случайного процесса через линейные цепи является спектральный метод. Напомним, что спектральный метод основывается на представлении сигнала в частотной области и знании комплексного коэффициента передачи цепи. Но если спектральный состав детерминированного сигнала определяется совокупностью комплексных амплитуд, то спектральный состав случайного сигнала определяется совокупностью значений мощности составляющих спектра, распределенных в диапазоне частот. В этом состоит особенность использования спектрального метода при анализе преобразования случайного сигнала линейной цепью.
Общая задача анализа прохождения случайного процесса через линейную цепь формулируется следующим образом. На вход линейной цепи (рис. 6.1) с комплексным коэффициентом передачи поступает случайный процесс , энергетический спектр которого (спектральная плотность мощности) равен . Необходимо найти характеристики случайного процесса на выходе линейной цепи.
Введем следующие предположения:
– входной случайный процесс является стационарным в широком смысле;
– среднее значение входного СП равно нулю, т.е. ;
– известен энергетический спектр входного процесса.
В соответствии с общим определением спектральной плотности мощности эта характеристика для выходного СП будет равна
. (6.1)
Величину можно представить следующим образом
, (6.2)
где – спектр реализации случайного процесса достаточно большой (теоретически бесконечной) длительности . С другой стороны, в предположении того, что реализация известна можно записать
, (6.3)
.
Подстановка (6.3) в (6.2) дает
. (6.4)
В свою очередь, подставляя (6.4) в (6.1), получим
. (6.5)
Таким образом, энергетический спектр случайного процесса на выходе линейной цепи равен произведению энергетического спектра входного случайного процесса и квадрата амплитудно–частотной характеристики цепи.
Выражение (6.5) определяет закон преобразования СП линейной цепью. Отметим, что фазо–частотная характеристика цепи не оказывает никакого влияния на этот закон.
Автокорреляционная функция выходного СП определяется в соответствии с теоремой Винера–Хинчина
![]() .
.
(в нашем случае автокорреляционная – корреляционной функции)
Так как дисперсия (средняя мощность) численно равна значению АКФ при , то для выходного СП можно записать
. (6.7)
Если входной СП имеет математическое ожидание, отличное от нуля, то математическое ожидание выходного СП определяется следующим выражением
. (6.8)
![]() ,при
,при
![]()
Поскольку для рассматриваемой задачи (см. предположения), то математическое ожидание .
Временной метод
Воспользуемся формулой, полученной
выше: ![]()
![]() ;
;
![]() ;
;
![]() ;
;
![]()
![]() - спектральная плотность импульсной
характеристики
- спектральная плотность импульсной
характеристики


Т.о.
![]()

Существуют приближенные методы решения задачи, которые учитывают специфические особенности вероятностных характеристик входного случ. процесса.