Следящие системы переменного тока, работающие на несущей частоте

Механизмы, к которым не предъявляются требования ра­боты с повышенной точностью, с успехом могут снабжаться весьма простыми следящими приводами переменного тока, функционирующими на несущей частоте. В этих приводах ис­пользуются наиболее простые по конструкции двухфазные дви­гатели с короткозамкнутым или полым ротором. В качестве из­мерителей рассогласования применяются сельсины или враща­ющиеся трансформаторы, включенные по трансформаторной схеме. На выходе сельсина-приемника при этом создается сиг­нал, который представляет собой модулированное по величине угла рассогласования напряжение переменного тока. Несущее напряжение имеет промышленную частоту 50 Гц или в авто­номных и бортовых установках (с индивидуальным источником питания) повышенную частоту 400 Гц. Двухфазный двигатель выполняет не только функции двигателя, но одновременно является демодулятором. Его скорость определяется амплитудой модулированного напряжения на обмотке управления. При этих условиях весь тракт усиления может быть выполнен полностью на переменном токе. Следовательно, отпадает отрицательное свойство усилителей постоянного тока -дрейф нуля. Усилители переменного тока в работе более стабильны.

Структура системы получается единообразной (рис. 6); все элементы ее работают на переменном токе - на несущей частоте -частоте питания. Однако в этих системах весьма затруднено ис­пользование корректирующих средств как в последовательной цепи, так и в цепях обратных связей. Обычные корректирующие средства, используемые в системах управления постоянного тока, здесь неприменимы. Поясним это на примере диф­ференцирующего звена. Предположим, что на вход дифферен­цирующего звена поступает сигнал

Рис. 6. Система на несущей частоте

1 -измеритель рассогласования (он же модулятор); 2, 3, 5, 6 - звенья системы; 4 - дифференциальное звено; 7-объект (он же демодулятор); 8- ТГ

x_вх = U(t)sinΩt (6.4)

где Ω - несущая частота в системе; U(t) - модулирующее напря­жение (полезный сигнал).

Тогда при идеальном дифференцировании будем иметь

x_вых=dx_вых /dt=U^’(t)sinΩt + U(t)ΩcosΩt

Следовательно, на выходе наряду с полезным сигналом, про­порциональным производной от входного воздействия, появит­ся квадратурная составляющая, смещенная по фазе на угол π/2. При этом ее амплитуда может быть намного больше амплитуды полезного сигнала, так как в качестве сомножителя в ее величину входит несущая частота Ω. В итоге квадратурная составляющая может забить полезный сигнал.

Представим сигнал на входе корректирующего звена как

x_вх=U(t)e^-jΩt

Для неискаженного преобразования необходимо, чтобы кор­ректирующее звено преобразовало лишь огибающую, не влияя на функцию e^-jΩt.

В связи с изложенным в системах переменного тока должны использоваться специальные корректирующие средства, кото­рые могут работать на несущей частоте, однако их применение связано с рядом технических трудностей, рассмотренных ниже. Поэтому весьма часто внутри системы используется блок, со­стоящий из демодулятора и модулятора (рис. 7), между кото­рыми после соответствующего фильтра включаются обычные корректирующие звенья постоянного тока. Наличие фильтра отрицательно влияет на динамику системы, так как вызывает дополнительный фазовый сдвиг. Однако он, безусловно, необхо­дим, причем его роль особенно существенна при частоте питания

Рис. 7. Система переменного тока с блоком демодулятор – модулятор (блок А)

2 - усилитель; 3 - демодулятор; 4 - фильтр; 6 - корректирующее звено; 7 - моду­лятор; 8-усилитель; 9-двигатель; 10-тахогенератор; 11-демодулятор; 12-фильтр; 13 - корректирующее звено в цепи обратной связи

400 Гц. Гармонические составляющие после дифференцирования могут создавать существенные помехи. Высокие требования предъявляются также к синусоидальности питающего напряже­ния. Гармонические составляющие в напряжении питания тоже генерируют помехи, которые после дифференцирования могут быть весьма значительными. Если в цепи обратной связи исполь­зуется асинхронный тахогенератор, то последовательно в его цепь до корректирующего звена тоже должен быть включен де­модулятор.

Расчет корректирующих звеньев и синтез систем с блоками демодулятор - модулятор практически не отличается от соответ­ствующего расчета для системы постоянного тока.

Рассмотрим теперь принципы построения корректирующих звеньев, работающих непосредственно на несущей частоте Ω.. Положим, что полезный сигнал изменяется по периодиче­скому закону с частотой _с т. е.

U(t) = U_maxsin ω_ct (6.6)

Тогда на входе корректирующего звена будем иметь напря­жение

u_вх = U_max sin ω_ct · sin Ωt (6.7)

или

u_вх = U_max /2 [cos (Ω - ω_c)t – cos(Ω + ω_c)t] (6.8)

т. е. входной сигнал может быть представлен двумя гармони­ческими составляющими с частотами, равными сумме и разности несущей частоты и частоты полезного сигнала. Запишем переда­точную функцию корректирующего звена как

W(jω) = W(ω)e ^jψ (6.9)

где W(ω) - амплитудная частотная характеристика;

ψ(ω) - фазо­вая характеристика.

Для нормальной неискаженной работы корректирующего звена необходимо, чтобы эти характеристики были симмет­ричны относительно точки, соответствующей несущей частоте Ω и вертикальной оси, проходящей через эту точку (рис.8). Условие симметрии амплитудной характеристики (четная характеристика) относительно оси, проходящей через точку Ω, может быть представлена как

W(Ω – ω_c) = W(Ω + ω_c) (6.10)

Для фазовой характеристики (нечетной) соответствующее условие центральной симметрии будет

ψ(Ω – ω_c) = – ψ(Ω + ω_c). (6.11)

При отсутствии симметрии появится квадратурная составля­ющая, искажающая преобразование сигнала.

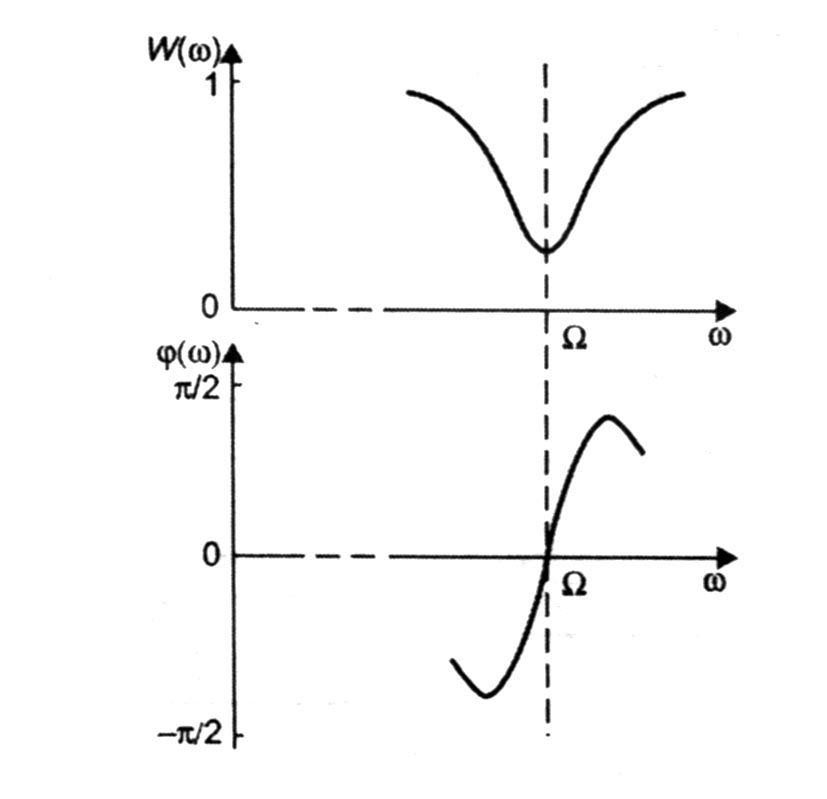
Рис. 8. Амплитудная и фазовая характеристики корректирующего (форсирующего) звена, работающего на переменном токе

Характеристики W(Ω + ω_c) и ψ(Ω + ω_c), перенесенные в начало координат, одновременно являются зависимостями для ампли­туды и фазы модулирующего сигнала W(ω_c) и ψ(ω_c). Следова­тельно, в системе на несущей частоте характеристики корректирующего звена постоянного тока как бы смещаются по оси час­тот в точку, соответствующую несущей частоте. Таким образом, если синтезировано корректирующее звено для работы в системе постоянного тока, то для того, чтобы перейти к звену, работа­ющему на несущей частоте, достаточно в выражении для передаточной функции W(ω_c) заменить ω_c на Ω + ω_c.

Рассмотрим некоторые частные примеры синтеза корректи­рующих звеньев переменного тока. Форсирующее звено, исполь­зуемое в системах постоянного тока, обычно строится по схеме рис. 9, а. При этом его передаточная функция имеет вид

W(p) = ρ(1 + Tp)/(1+ρTp) (6.12)

где T = r₁C; ρ = r₂ / (r₁ + r₂)

При работе на несущей частоте контур должен представлять собой полосовой фильтр, настроенный на несущую частоту, при этом конденсатор заменяется параллельным соединением индуктивности и емкости (рис. 9, б). Передаточная функция такого звена будет

W(p) = r­₂/(r₂ + (r₁Lp)/(r₁ + Lp + r₁LCp²)) =

= (r₂[T₁T₂p² + T₁p + 1])/(r₂[r₂[T₁T₂p² + T₁p + 1] + r₁T₁p) =

= (r₂/r₁ + r₂) · (T₁T₂p² + T₁p + 1)/((r₂/ r₁ + r₂)[ T₁T₂p² + 1] + T₁p) (6.13)

где T₁ = L / r₁ ; T₂ = r₁C

Рис. 9. Схемы форсирующих звеньев (1-й вариант): а - на постоянном токе; б –на несущей частоте

Соответственно при резонансе

LC=T₁T₂ = 1/Ω²

где Ω - несущая частота.

Обозначив дополнительно r₂ / (r₁ + r₂) = ρ, получим

W(p) = (ρ((1/Ω²)p² + T₁p 1)) / (ρ((1/Ω²)p² + 1) + T₁p) (6.14)

Перейдем теперь к частотным характеристикам. Заменив

p = jω = j(Ω + ω_c), (6.15)

Получим

W(jω) = (ρ((ω²/Ω²) + jωT₁ + 1)) / (ρ((–ω²/Ω²) + 1) + jωT₁)) =

= (ρ((Ω² – (Ω + ω­_c)² + j(Ω + ω_c) ΩT₁)) / (ρ[Ω² – (Ω + ω­_c)² ] + j(Ω + ω_c) ΩT₁) =

= (ρ(–(2Ω + ω_c)ω_c + j(Ω + ω_c)Ω²T₁)) / (–ρ(2Ω + ω_c)ω_c + j(Ω + ω_c)Ω²T₁), (6.16)

Так как Ω » ω_с, то без большой погрешности ω_с в круглых скобках можно не учитывать и соответственно можем написать

W(jω) = (ρ(2ω_c – jΩ²T₁)) / (ρ · 2ω_c – jΩ²T₁) (6.17)

Умножив числитель и знаменатель на j, получим

W(jω) = (ρ(2Ω²T₁ + j · 2ω_c )) / (2Ω²T₁ + j · 2ρω_c ) =

= (ρ(1 + (2ω_c / Ω²T₁)) / (1 + jρ(2ρω_c / Ω²T₁ )) (6.18)

Если обозначить 2/ Ω²T₁ = Т, то окончательно получим

W(jω) = (ρ(1 + jω_cT))/ (1 + jω_cρT) (6.19)

Найденное выражение адекватно аналогичному выражению для реального форсирующего звена, широко используемого в сле­дящих системах постоянного тока.

Так как Ω² = 1/LC, то также можем написать

Т=Т_п= 2r₁LC/L = 2r₁C = 2T_н (6.20)

или T_н = Т_п/2. Здесь индекс "п" соответствует корректирующему звену, работающему на постоянном токе (для моделирующего сигнала); "н" -тоже на несущей частоте. Следовательно, емкость в звене, работающем на несущей частоте, должна быть в два раза меньше, чем в звене, работающем на постоянном токе, т. е. С_н = С/2, а индуктивность L_н = 2/Ω²C = 2L. Резисторы остаются неизменными.

Следует отметить, что схема рис. 9, б практически не исполь­зуется, так как для нее необходима катушка индуктивности с весь­ма большой добротностью. Практически применяется корректи­рующее звено (рис. 10, б), аналогичное корректирующему звену (рис. 10, а). В системах постоянного тока последнее используется редко, так как введение в схему катушки индук­тивности вообще нежелательно (большие габариты, нелиней­ность характеристики, нагрев и т. п.). В цепях переменного тока применение катушек индуктивности становится необходимым, а требование по ее добротности для схемы (рис. 10, 6) ниже, чем для схемы (рис. 9, 6).

Частотная передаточная функция рассматриваемого вто­рого варианта корректирующего звена описывается выраже­нием (20), причем в этом случае

L_н = L/2, а С_н = 2/ Ω²C

Трудности изготовления катушек индуктивности с высокой добротностью и линейными характеристиками обусловили от­каз от простейших схем корректирующих звеньев, аналогичных схемам, используемым на постоянном токе, и переход к мосто­вым схемам, построенным целиком на элементах rC (рис. 10).

Передаточная функция Т-образной мостовой схемы имеет тот же вид (19). При этом

ρ = 2r₂/(2r₂ + r₁) = r₂/(r₂ + (r₁/2)), T = T_п = 1/r₂CΩ²

Рис, 10. Схемы форсиру- Рис. 11. Мостовые схемы корректи-

ющих звеньев (2-й вариант) рующих звеньев: а - Т-образная

схема; б - двойной Т-образный мост

и соответственно

ρT = 1/((r₂ + (r₁ /r₂))CΩ²)

Та же передаточная функция относится и к двойному Т- образному мосту, но в этом случае

ρ = (2 ­­­­­­­­­­­­­– γ)/(2 + γ + γ²); T = 2γ/((2 – γ)Ω); ρT = 2γ/(2 + γ + γ²)Ω

Если имеем настроенный мост, т. е. γ = 2, то ρ → 0, а T → ∞,

при этом постоянная ρТ приобретает фиксированное значение ρT= 1/2Ω.

В передаточной функции звена в этом случае можно пренебречь единицей по сравнению с jω_cT. Обозначив ρT = T_д, получим

W(jω) = (ρjω_cT)/(1 + jω_c ρT) = (jω_c T_д)/(1 + jω_c T_д) (6.21)

т. е. этот фильтр не пропускает составляющую, пропорциональ­ную входному воздействию и превращается в дифференциру­ющее звено с отставанием. Ему соответствует на постоянном то­ке звено, схема которого представлена на рис. 12. В связи с этим, если звено вводится последовательно в основ­ную цепь, то его приходится видоизменять и использовать дополнительно делитель напряже­ния (рис.13).

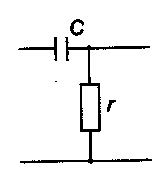
Рис. 12. Дифференцирующее звено для коррекции на постоянном токе

Рис. 13. Двойной Т-образный мост, используемый как форсирующее звено

Корректирующие звенья переменного тока весьма чувстви­тельны как к уходу несущей частоты, так и к нестабильности параметров самого звена. В обоих случаях на выходе появляется квадратурная составляющая, которая по величине может быть больше полезной. Следует иметь в виду, что более жесткие требования к стабильности частоты предъявляются в системах, работающих на частоте 400 Гц (по сравнению с 50 Гц), так как здесь важно не относительное изменение частоты, а абсолютное значение его отклонения, сопоставимое с частотой полезного модулирующего сигнала.

Для систем на промышленной частоте 50 Гц отклонение ча­стоты не должно превышать 1-2%. Параметры корректирующих цепей подбираются с погрешностью, не превышающей 0,5-1% относительно расчетных значений.

Приведенные соображения в отдельных случаях приводят к необходимости применения адаптивных корректирующих цепей. При этом используется то обстоятельство, что при изменении знака ухода частоты фаза квадратурной составляющей изменяется на я.

Сложность настройки корректирующих звеньев, работа­ющих на несущей частоте, вынуждает использовать корректиру­ющие звенья постоянного тока, применяя схему демодулятор -фильтр - корректирующее звено - модулятор. В качестве модуля­тора обычно используется сам исполнительный двигатель.

Лекция 9