Методика прогнозирования показателей здоровья населения с использованием метода экстраполяции

Экстраполяция – процесс прогноза события на основе анализа показателей предыдущих лет.

Этот метод может использоваться при наличии данных об уровне явления за 2 года, в этом случае прогноз носит ориентировочный характер. Более точный прогноз возможен при использовании экстраполяции на основе сведений об уровне явления, полученных в результате анализа его в процессе развития (по данным динамического ряда).

Применение метода экстраполяции при прогнозировании уровней заболеваемости по двум точкам

Для прогнозирования уровней заболеваемости по двум точкам используется следующая формула:

P _t= P₁ + T ×

где P_t - прогнозируемый уровень;

P_{1 –} показатель заболеваемости за один из предыдущих годов (более близкий к прогнозируемому)

P₀ - показатель заболеваемости за другой предшествующий год (более отдаленный от прогнозируемого)

n – период между 2 исследованиями (2 предшествующими годами)

Т - период между моментом получения последнего результата и годом прогнозирования (в годах).

Например, уровни заболеваемости населения туберкулезом (на 100 000) в 1995-2003 гг. составили: 1995 – 43,9; 1996 – 48,9; 1997 – 52,8; 1998 – 54,9; 1999 – 53,6; 2000 – 49,9; 2001 – 47,5; 2002 – 51,8; 2003 – 51,7 Следует определить прогнозируемый уровень заболеваемости туберкулезом на 2005 г. на основании данных о заболеваемости в 2000 и 2003 гг.

P _t=51,7+2 × = 51,7 + 2 × 1,4 = 54,5 %ооо

Прогнозируемый уровень заболеваемости туберкулезом в 2005г. составляет 54,5 случая на 100 000 населения.

Применение метода экстраполяции при прогнозировании уровней заболеваемости по данным динамического ряда

Прогнозирование показателей заболеваемости по данным динамического ряда осуществляется после выравнивания последнего и выявления тенденции изучаемого явления.

Многолетние тенденции в зависимости от характера обусловливающих их причин могут быть прямо- или криволинейными. Прямолинейная тенденция указывает на равномерное изменение интенсивности явления. Если причины, формирующие тенденцию явления действуют неравномерно и эффект их действия постепенно уменьшается или возрастает, то тенденции приобретают криволинейную форму.

Для оценки тенденции процесса необходимо подобрать соответствующее уравнение, наиболее точно отражающее подлинную динамику данного процесса. Существует множество уравнений, с помощью которых описываются различные тенденции. Наиболее часто используется уравнение линейной зависимости (или парабола первого порядка), которое позволяет провести выравнивание данных динамического ряда по прямой. В некоторых случаях развитие явления можно отразить линией, описываемой параболой 2-ого, 3-его т.д. порядка.

Выравнивание показателей динамического ряда по прямой основано на математическом законе, согласно которому при прямолинейной тенденции через ряд эмпирических точек можно провести только одну прямую, отвечающую требованию: сумма квадратов отклонений фактических данных от выровненных будет наименьшей. При помощи этого способа находят линию, которая наиболее точно отражает эмпирические данные и характеризует направление изучаемого явления.

Для выравнивания динамического ряда показателей заболеваемости по прямой используется уравнение линейной зависимости (парабола первого порядка):

P _теор = A + B × X,

где P _теор - теоретические (расчетные) уровни заболеваемости за каждый год динамического ряда после выравнивания, которые необходимы для построения линии тенденции:

A – среднеарифметический уровень заболеваемости за изучаемый период;

В – коэффициент, отражающий разницу между теоретическими уровнями заболеваемости за смежные годы (указывает направление и величину тенденции);

Х – преобразованный интервал в виде натуральных чисел, проставленных от центра ряда в оба его конца.

Например, заболеваемость населения Республики Беларусь злокачественными новообразованиями (на 100 000 населения) составляла:

1995 г – 296,1; 1996 – 314,9; 1997 – 319,1; 1998 – 329,6; 1999 – 327,5; 2000 – 330,5; 2001 – 340,5; 2002 – 346,5; 2003 – 351,0. Численность населения в 2003 году была 9849100 человек. Следует определить прогнозируемый уровень заболеваемости населения злокачественными новообразованиями в 2005 году.

Алгоритм расчетов

1. Данные о заболеваемости изображаются графически в виде линейной диаграммы. По внешнему виду ломаной кривой можно предположить наличие прямой линейной зависимости.

2. Определяется середина изучаемого ряда. При данном числе изучаемых лет (N = 9) серединой ряда будет 5-й (1999) год. Для этого значения пишется «0». Если число наблюдений четное (например, 8) серединой ряда будет 4-й и 5-й годы, причем для 4-го года проставляется натуральное число «-1», а для 5-го – «+1».

3. От середины ряда в оба конца последовательно проставляются натуральные числа ( Х ). При нечетном числе лет (например, 9) проставляются числа -1; -2; -3; -4 от середины ряда в сторону меньших значений и числа +1; +2; +3; +4 в сторону больших значений (в нашем примере при нечетном числе лет – с разницей в 1). При четном числе лет (например, 8) последовательно проставляются числа -1; -3; -5; -7 от середины ряда в сторону меньших значений и числа +1; +3; +5; +7 от середины ряда в сторону больших значений (с разницей в 2).

4. Для каждого года рассчитывается произведение натурального числа ( Х ) на фактический показатель заболеваемости ( P_факт ), полученные произведения ( Х × P_факт ) суммируются.

5. Определяются квадраты натуральных чисел ( Х ² ) и их сумма ∑ ( Х ² ).

6. Рассчитываются значения А и В по формулам:

А = ; В =

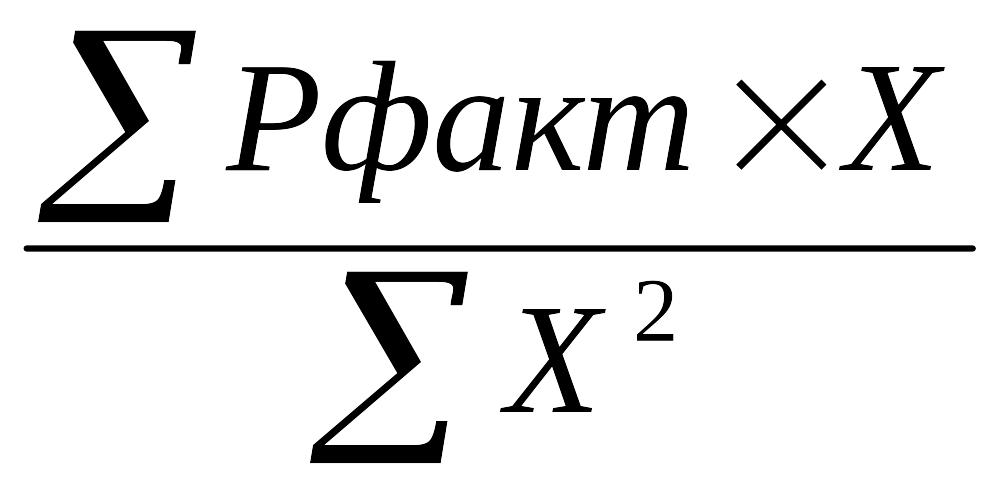
7. Для каждого года определяются теоретические значения заболеваемости (P _теор). С этой целью полученные значения А и В подставляют в уравнение (P_теор = A + B × X) и последовательно придают значения натуральных чисел для Х.

8. Полученные теоретические значения показателей заболеваемости наносят на график и соединяют прямой линией, направленной вверх или вниз по отношению к оси абсцисс в зависимости от направления тенденции изучаемого явления.

9. Оценка соотношения кривой фактической заболеваемости и линии тенденции позволяет сформулировать выводы о росте, стабилизации или снижении заболеваемости. Многолетнюю тенденцию характеризуют по ее направленности и скорости изменения уровней динамического ряда. Направление тенденции (рост, снижение ) определяют по знаку при коэффициенте ( В ) в уравнении, которое ее описывает. При наличии знака « - » при коэффициенте В характерна тенденция к снижению, если коэффициент В имеет знак « + » проявляется тенденция к росту.

7. Скорость изменений в динамическом ряду оценивают по показателям роста и прироста.

Для обобщающей количественной оценки тенденции динамического ряда используется средний показатель среднего темпа прироста, выраженный в процентах. Он характеризует среднюю скорость изменения уровня заболеваемости в динамическом ряду и является относительной оценкой скорости изменений уровня ряда. Рассчитывают его на основании значений теоретической линии тенденции:

Т пр. ср. = × 100 %

Оценка среднего темпа изменений ряда проводится следующим образом:

- при Т _{пр. ср.} от 0 до ± 1 % тенденция считается стабильной;

- при Т _{пр. ср.} от ± 1 % до ± 5 % - умеренной;

- при Т _{пр. ср.} свыше ± 5 % - выраженной.

11. После выравнивания динамического ряда по прямой оценивается правильность выбора уравнения регрессии.

Необходимым условием для прогнозирования методом экстраполяции является выбор соответствующего уравнения регрессии, наиболее точно отражающего динамику исследуемого процесса. Для оценки точности аппроксимации (соответствия выбора) уравнения регрессии рассчитывается величина σ.

σ = × 100%,

где d = Р факт. – Ртеор.

Чем меньше эта величина, тем выше точность аппроксимации, т.е. тем точнее подобрано уравнение регрессии для описания наметившейся тенденции в динамике заболеваемости.

Если значения достаточно велики, следует провести выравнивание по параболе 2-го, 3-го и т.д. порядков, но в санитарной статистике потребность в них бывает относительно редко. Из рассчитанных значений точности аппроксимации выбирается самый меньший из показателей и определяется уравнение, наиболее точно характеризующее динамику изучаемого явления.

12. Расчет прогнозируемого уровня заболеваемости методом экстраполяции.

Прогноз заболеваемости на следующий год осуществляется путем определения теоретического прогнозируемого уровня заболеваемости ( P_{прог. теор} ) и его доверительных границ на прогнозируемый год.

Теоретический прогнозируемый уровень заболеваемости определяется путем продолжения линии тенденции ее на графике до вертикали, идущей от оси абсцисс из точки, соответствующей прогнозируемому году. Из точки пересечения линии тенденции и вертикали опускается перпендикуляр на ось ординат, на которой определяется прогнозируемая величина уровня заболеваемости.

Теоретический прогнозируемый уровень заболеваемости можно определить также путем расчетов по формуле:

P_{прог. теор} = A + B × X (nk),

где X (nk) – значение натурального числа, соответствующего году прогнозирования. В нашем примере при прогнозировании уровня заболеваемости на 2005г. при наличии ряда показателей заболеваемости с нечетным числом лет значение X (пк) будет соответствовать натуральному числу +6, и с четным числом лет - +11.

13. Доверительные границы теоретического прогнозируемого уровня заболеваемости определяется по формуле:

P_прог. = P_{прог. теор} + t × m,

где t – критерий Стьюдента, соответствующий выбранному уровню безошибочного прогноза (в медико-биологических исследованиях обычно применяется вероятность безошибочного прогноза, равная 95%, для которой t=2).

m – средняя ошибка теоретического прогнозируемого уровня заболеваемости; рассчитывается она по формуле:

m= ± ,

где Р – теоретический прогнозируемый уровень (P_{прог. теор});

q – разность между размерностью показателя и самим показателем (если показатель заболеваемости рассчитан на 100 000, то q = 100 000 - P_{прог. теор});

N – численность населения.

Выравнивание динамического ряда показателей заболеваемости и других показателей здоровья, а также прогнозирование их уровней можно проводить на ПЭВМ с использованием прикладных программ для статистической обработки. Это позволяет быстро решить задачу, получить высокую точность результатов, значительно сократить время на статистическую обработку данных. Вычисления можно осуществлять также с помощью программируемых микрокалькуляторов. Это удобные средства индивидуального пользования.

69