
- •1.Коньюнкция условий и разбиение пространства входа.
- •Композиция нечетких отношений.
- •Нечеткое инверсное управление и нечеткая система управления с внутренней моделью
- •Алгоритм жесткой кластеризации.
- •Операции над нечеткими множествами. Модификаторы.
- •8. Проектирование нечетких контроллеров (метод Мамдани)
- •2. Нечеткий контроллер с двумя входами и одним выходом
- •9.Нечеткая система управления с плановым изменением коэффициента.
- •10. Оценка параметров заключений по (мнк)
- •11. Адаптивные нейронные нечеткие системы инференции (anfis)
- •12.Импликация Мамдани. Внешнее произведение.Таблица импликаци
- •13. Нечеткая идентификация. Структура и параметры.
- •14. Нечеткий логический вывод для нескольких правил и нескольких входов.
- •Несколько входов (многомерная лингвистическая модель)
- •16. Функциональная схема нечеткого контроллера
- •17. Отношения между нечеткими множествами
- •18. Алгоритм нечеткой кластеризации с-средних
- •19. Моделирование статических объектов упр-я как аппроксимация функций с помощью нейронных сетей (есть только для динамических объектов)((((((((
- •20. Анализ устойчивости тс модели объекта управления в пространстве состояний.
- •22. Нечеткий логический вывод с исп-м отношений. Пример
- •24. Визуализация алгоритма нечеткого логического вывода.
- •25. Понятия о нечетких множествах
- •26. Обучение нейронной сети. Общие сведения.
- •27. Упрощение алгоритма нечеткого логического вывода.
- •28. Обратное распространение ошибки
- •29. Визуализация нечеткого логического вывода.Аккумуляция.
- •30. Параметры алгоритма с-средних
- •31. Проектирование нечетких контроллеров (метод Мамдани)
- •32. Нечеткая логика. Логические связки.
- •33.Проектирование нечетких контроллеров(метод Мамдани). Многомерный нечеткий контроллер.
- •34. Алгоритм обучения anfis
- •35. Максиминная композиция нечетких отношений. Внутренне произведение. Пример.
- •36. Преобразование вход-выход. Кривая управления. Пов-ть управления.
- •37. Табличное изменение коэффициента усиления (супервизорное управление)
- •38. Алгоритм нечеткой кластеризации Густафсона–Кесселя.
- •39. Генетические алгоритмы
- •40. Извлечение правил с помощью кластеризации
- •41.Нечеткий сумматор для контроллеров с 2 входами и 1 выходом
- •42. Нейросетевое прямое и косвенное адаптивное управление с эталонной моделью
- •43. Обратное распространение ошибки. Обновление весовых коэф-в скрытых слоев. Локальные градиенты.
- •44. Модель Такаги-Сугено как квазилинейное устройство
- •45. Контроллер типа Такаги-Сугено
- •46. Нейросетевое управление с адаптивной линеаризацией обратной связью
- •48. Такаги-Сугено модель оу в пространстве состояний
- •49. Нечеткие множества. Синглтоны и лингвистические переменные.
- •50. Моделирование нелинейных динамических оу с помощью нейронных сетей
- •51. Структура интеллектуальной системы управления
- •52. Многослойная нейронная сеть
- •53. Дефаззификация. Методы дефаззификации.
- •54. Нейронная сеть с радиальными базисными функциями
- •56. Синтез нечеткой обратной связи
- •57. Линейные матричные неравенства, основные понятия.
- •58. Аппроксимация функций (моделирование) с помощью нейронных сетей (персептронов)
- •59. Классификация генетических нечетких систем
- •60. Синтез нейронных нечетких сетей. Структура anfis
- •19. Моделирование статических объектов управления как аппроксимация функций с помощью нейронных сетей.
- •Адаптивные нейронные нечеткие системы интерференции (anfis). . Синтез нечетких нейронных сетей
- •5.1. Введение
- •Адаптивные нейронечеткие системы инференции (anfis)
- •Импликация Мамдани. Внешнее произведение. Таблица импликации.
- •Нечеткая идентификация. Структура и параметры
- •Нечеткий логический вывод для нескольких правил и нескольких входов.
- •1. Настройка пид-регулятора
- •3. Перенос параметров пид-регулятора в нечеткий контроллер
- •Анализ устойчивости тс модели объекта управления в пространстве состояний. Анализ устойчивости тс модели объекта
- •1. Настройка пид-регулятора
- •Нечеткий логический вывод (инференция). Пример.
- •Визуализация нечеткого логического вывода. Агрегирование условий и активизация заключений.
- •Математическая модель нейрона. Математическая модель нейрона
- •Нечеткое управление с предсказанием.
- •Визуализация нечеткого логического вывода. Аккумуляция заключений.
- •5.1. Введение
- •Алгоритм обучения anfis
- •Максиминная композиция нечетких отношений. Внутреннее произведение. Пример.
- •Преобразование вход-выход для нечетких контроллеров. Кривая управления и поверхность управления.
- •2.4. Преобразование вход-выход
- •Табличное изменениекоэффициентаусиления (супервизорное управление).
- •2.8. Табличное изменение коэффициента усиления (супервизорное управление)
- •Алгоритм нечеткой кластеризации Густафсона-Кесселя.
- •Генетические алгоритмы. Генетические алгоритмы
- •Модель Такаги-Сугено как квазилинейное (аффинное) устройство. Модель Такаги-Сугено как квазилинейное устройство
- •Контроллер типа Такаги-Сугено.
- •Деффазификация. Методы деффазификации.
- •2.2.5. Дефаззификация
- •Теорема б универсальной аппроксимации.
- •Такаги-Сугено модель объекта управления в пространстве состояний.
- •Табличный контроллер. Билинейная интерполяция.
- •2.3. Табличный контроллер
- •Моделирование нелинейных динамических объектов управления с помощью нейронных сетей.
- •Моделирование нелинейных динамических процессов (объектов)
- •Упрощение алгоритма нечеткого логического вывода.
- •Обратное распространение ошибки. Обновление весовых коэффициентов выходного слоя.
- •4.6. Обратное распространение ошибки
- •Структура интеллектуальной системы управления.
- •Многослойная нейронная сеть. Многослойная нейронная сеть
- •5.1. Введение
- •Структура anfis
9.Нечеткая система управления с плановым изменением коэффициента.
Н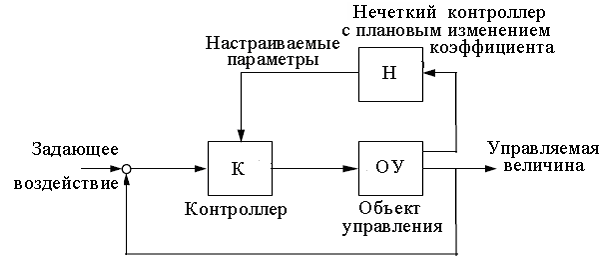 ечеткие
правила могут быть использованы также
для подстройки (коррекции) параметров
управляющего устройства (контроллера)
в адаптивных параметрических системах
управления. Если меняется рабочая
точка нелинейного объекта управления
(величина задающего воздействия в
промышленных системах управления), то
в принципе можно изменять параметры
контроллера применительно к каждому
новому значению рабочей точки.Этот
закон управления получил название
плановое (табличное) изменение
коэффициента (gain
scheduling) [10], т.к.
первоначально данный закон применялся
для изменения коэффициента усиления
контроллера в соответствии с заранее
рассчитанными и внесенными в таблицу
его (коэффициента усиления) значениями.
Контроллер с плановым изменением
коэффициента содержит линейный контроллер
K, параметры которого
изменяются как функция координат
рабочей точки. Разумеется, эта функция
предварительно определена и
запрограммирована, для чего требуется
всестороннее знание свойств объекта
управления. Тем не менее, описанный
подход во многих случаях является
эффективным способом уменьшения влияния
на управляемую величину нелинейностей
и вариации параметров ОУ. Измерения
выхода, полученные с помощью датчика,
используются как плановые переменные,
управляющие изменением параметров
контроллера, часто за счет применения
табличной формы, которая представляет
значения параметров как функции координат
рабочей точки.
ечеткие
правила могут быть использованы также
для подстройки (коррекции) параметров
управляющего устройства (контроллера)
в адаптивных параметрических системах
управления. Если меняется рабочая
точка нелинейного объекта управления
(величина задающего воздействия в
промышленных системах управления), то
в принципе можно изменять параметры
контроллера применительно к каждому
новому значению рабочей точки.Этот
закон управления получил название
плановое (табличное) изменение
коэффициента (gain
scheduling) [10], т.к.
первоначально данный закон применялся
для изменения коэффициента усиления
контроллера в соответствии с заранее
рассчитанными и внесенными в таблицу
его (коэффициента усиления) значениями.
Контроллер с плановым изменением
коэффициента содержит линейный контроллер
K, параметры которого
изменяются как функция координат
рабочей точки. Разумеется, эта функция
предварительно определена и
запрограммирована, для чего требуется
всестороннее знание свойств объекта
управления. Тем не менее, описанный
подход во многих случаях является
эффективным способом уменьшения влияния
на управляемую величину нелинейностей
и вариации параметров ОУ. Измерения
выхода, полученные с помощью датчика,
используются как плановые переменные,
управляющие изменением параметров
контроллера, часто за счет применения
табличной формы, которая представляет
значения параметров как функции координат
рабочей точки.
С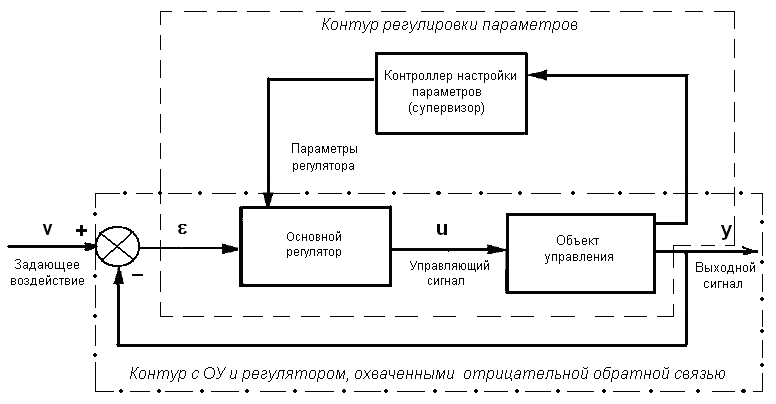
 истемы
с плановым изменением коэффициента
усиления (изменение осуществляется
программно) используются в случаях,
когда математическая модель системы
является линейной только в определенном
диапазоне изменения входного сигнала
(задающего воздействия v)
и при изменении условий работы она может
стать нелинейной. Таким образом, в ряде
ситуаций наиболее точным оказывается
описание системы с помощью нелинейных
математических моделей. Рассмотрим
схему системы с плановым изменением
коэффициента усиления [1,2]. Она представляет
собой два контура (рис. 1): один контур
(показан штрих-пунктиром) – нелинейный
объект управления и регулятор (далее
будем называть его основным), охваченные
отрицательной обратной связью; другой
контур (показан пунктиром) - контур
регулировки параметров основного
регулятора, включающий в себя нечеткий
супервизор, который и осуществляет, как
говорят, плановое
изменение коэффициента усиления.
Дело в том, что сначала использовали
супервизор лишь для настройки коэффициента
усиления оснеовного контура. В подобных
случаях целесообразно попытаться
использовать плановое изменение
коэффициента усиления. Это означает,
что каждому постоянному значению
входного сигнала v
(а, следовательно, и выходного y в
установившемся режиме) будут соответствовать
свои значения коэффициентов усиления
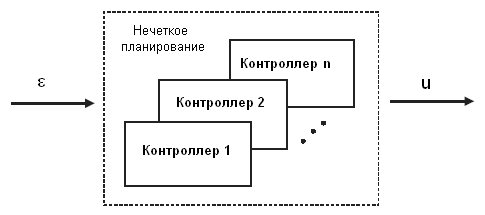
системы. При включении супервизора в
САУ с объектом управления, имеющим
сильно нелинейные свойства, внутренняя
структура основного регулятора может
быть представлена, как показано на рис.
4. При этом с помощью планового изменения
коэффициента усиления происходит
переключение между регуляторами,
находящимися внутри «пакета контроллеров»,
каждый из которых предназначен для
одной рабочей точки. Супервизор
определяет, какой из контроллеров
«Контроллерj
»,
истемы
с плановым изменением коэффициента
усиления (изменение осуществляется
программно) используются в случаях,
когда математическая модель системы
является линейной только в определенном
диапазоне изменения входного сигнала
(задающего воздействия v)
и при изменении условий работы она может
стать нелинейной. Таким образом, в ряде
ситуаций наиболее точным оказывается
описание системы с помощью нелинейных
математических моделей. Рассмотрим
схему системы с плановым изменением
коэффициента усиления [1,2]. Она представляет
собой два контура (рис. 1): один контур
(показан штрих-пунктиром) – нелинейный
объект управления и регулятор (далее
будем называть его основным), охваченные
отрицательной обратной связью; другой
контур (показан пунктиром) - контур
регулировки параметров основного
регулятора, включающий в себя нечеткий
супервизор, который и осуществляет, как
говорят, плановое
изменение коэффициента усиления.
Дело в том, что сначала использовали
супервизор лишь для настройки коэффициента
усиления оснеовного контура. В подобных
случаях целесообразно попытаться
использовать плановое изменение
коэффициента усиления. Это означает,
что каждому постоянному значению
входного сигнала v
(а, следовательно, и выходного y в
установившемся режиме) будут соответствовать
свои значения коэффициентов усиления
системы. При включении супервизора в
САУ с объектом управления, имеющим
сильно нелинейные свойства, внутренняя
структура основного регулятора может
быть представлена, как показано на рис.
4. При этом с помощью планового изменения
коэффициента усиления происходит
переключение между регуляторами,
находящимися внутри «пакета контроллеров»,
каждый из которых предназначен для
одной рабочей точки. Супервизор
определяет, какой из контроллеров
«Контроллерj
»,
![]() ,
будет использоваться в конкретной
области изменения входных и выходных
сигналов.
,
будет использоваться в конкретной
области изменения входных и выходных
сигналов.
П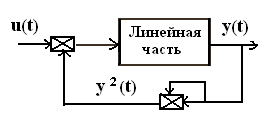 усть
существует объект управления с существенно
нелинейными свойствами (коэффициент
усиления объекта y2(t)
зависит от управляемой величины y(t)).
Структуру данного объекта можно
представить как линейную часть с ПФ,
охваченная квадратичной обратной
связью.
усть
существует объект управления с существенно
нелинейными свойствами (коэффициент
усиления объекта y2(t)
зависит от управляемой величины y(t)).
Структуру данного объекта можно
представить как линейную часть с ПФ,
охваченная квадратичной обратной
связью.
Цель управления заключается в том,
чтобы обеспечить стабилизацию системы
при изменении рабочей точки (состояния
равновесия) в широких пределах при
условии, что y![]() 0.
Проблемы, возникающие при использовании
для этой цели четкого пропорционального
регулятора с фиксированным коэффициентом
усиления kp,
сводятся к следующему:
0.
Проблемы, возникающие при использовании
для этой цели четкого пропорционального
регулятора с фиксированным коэффициентом
усиления kp,
сводятся к следующему:
устойчивость и качество системы в сильной степени зависят от значения управляемой величины в состоянии равновесия;
настройка (подбор) коэффициента усиления kp не позволяет добиться желаемой цели.
Отсюда приходим к выводу, что единственный путь решения поставленной задачи применить нелинейный закон управления, а именно, супервизорное управление, которое бы изменяло коэффициент усиления по нелинейному закону в зависимости от управляемой величины у.
Для реализации желаемого закона управления можно использовать различные способы аппроксимации, в частности, кусочно-линейную аппроксимацию или метод задания таблиц (look-up table) . Однако более удобно с точки зрения точности и быстроты вычислений применить нечеткий контроллер типа Такаги-Сугено. Заметим, что с помощью нечеткой логики можно, используя правила и функции принадлежности обеспечить аппроксимацию любой непрерывной функции с любой требуемой точностью, т.е. нечеткая модель при соответствующем выборе параметров является универсальным аппроксиматором.
А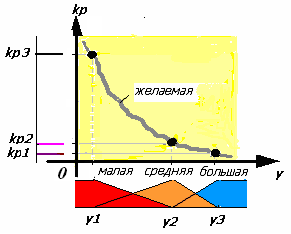 ппроксимируем
желаемую кривую изменения коэффициента
усиления регулятора, используя три
правила. Разумеется, чтобы повысить
точность аппроксимации можно добавить
еще правила, которые очевидно улучшат
качество управления. Нечеткий контроллер,
используемый для аппроксимации,
значительно проще реализовать и
настроить с помощью средств вычислительной
техники, чем таблицы задания и
кусочно-линейной аппроксимации.
ппроксимируем
желаемую кривую изменения коэффициента
усиления регулятора, используя три
правила. Разумеется, чтобы повысить
точность аппроксимации можно добавить
еще правила, которые очевидно улучшат
качество управления. Нечеткий контроллер,
используемый для аппроксимации,
значительно проще реализовать и
настроить с помощью средств вычислительной
техники, чем таблицы задания и
кусочно-линейной аппроксимации.
В данном случае базовые правила выглядят так:
Если управляемая величина y большая, То коэффициент kp1,
Если управляемая величина y средняя, То коэффициент kp2,
Е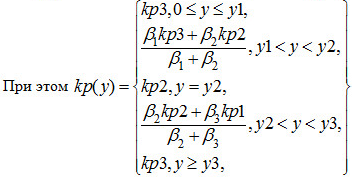 сли
управляемая величина y
малая, То коэффициент kp3.
сли
управляемая величина y
малая, То коэффициент kp3.
Разумно
спроектировать нечеткий супервизор,
на выходе которого формировалась бы
функция![]() .
При этом коэффициент пропорционального
регулятора целесообразно находить по
формуле
.
При этом коэффициент пропорционального
регулятора целесообразно находить по
формуле![]() где
где
![]() - коэффициент
усиления основного регулятора,
обеспечивающий выполнение заданных
требований в отношении перерегулирования
или времени регулирования для v(t)=1(t).
- коэффициент
усиления основного регулятора,
обеспечивающий выполнение заданных
требований в отношении перерегулирования
или времени регулирования для v(t)=1(t).

