
- •1.Коньюнкция условий и разбиение пространства входа.
- •Композиция нечетких отношений.
- •Нечеткое инверсное управление и нечеткая система управления с внутренней моделью
- •Алгоритм жесткой кластеризации.
- •Операции над нечеткими множествами. Модификаторы.
- •8. Проектирование нечетких контроллеров (метод Мамдани)
- •2. Нечеткий контроллер с двумя входами и одним выходом
- •9.Нечеткая система управления с плановым изменением коэффициента.
- •10. Оценка параметров заключений по (мнк)
- •11. Адаптивные нейронные нечеткие системы инференции (anfis)
- •12.Импликация Мамдани. Внешнее произведение.Таблица импликаци
- •13. Нечеткая идентификация. Структура и параметры.
- •14. Нечеткий логический вывод для нескольких правил и нескольких входов.
- •Несколько входов (многомерная лингвистическая модель)
- •16. Функциональная схема нечеткого контроллера
- •17. Отношения между нечеткими множествами
- •18. Алгоритм нечеткой кластеризации с-средних
- •19. Моделирование статических объектов упр-я как аппроксимация функций с помощью нейронных сетей (есть только для динамических объектов)((((((((
- •20. Анализ устойчивости тс модели объекта управления в пространстве состояний.
- •22. Нечеткий логический вывод с исп-м отношений. Пример
- •24. Визуализация алгоритма нечеткого логического вывода.
- •25. Понятия о нечетких множествах
- •26. Обучение нейронной сети. Общие сведения.
- •27. Упрощение алгоритма нечеткого логического вывода.
- •28. Обратное распространение ошибки
- •29. Визуализация нечеткого логического вывода.Аккумуляция.
- •30. Параметры алгоритма с-средних
- •31. Проектирование нечетких контроллеров (метод Мамдани)
- •32. Нечеткая логика. Логические связки.
- •33.Проектирование нечетких контроллеров(метод Мамдани). Многомерный нечеткий контроллер.
- •34. Алгоритм обучения anfis
- •35. Максиминная композиция нечетких отношений. Внутренне произведение. Пример.
- •36. Преобразование вход-выход. Кривая управления. Пов-ть управления.
- •37. Табличное изменение коэффициента усиления (супервизорное управление)
- •38. Алгоритм нечеткой кластеризации Густафсона–Кесселя.
- •39. Генетические алгоритмы
- •40. Извлечение правил с помощью кластеризации
- •41.Нечеткий сумматор для контроллеров с 2 входами и 1 выходом
- •42. Нейросетевое прямое и косвенное адаптивное управление с эталонной моделью
- •43. Обратное распространение ошибки. Обновление весовых коэф-в скрытых слоев. Локальные градиенты.
- •44. Модель Такаги-Сугено как квазилинейное устройство
- •45. Контроллер типа Такаги-Сугено
- •46. Нейросетевое управление с адаптивной линеаризацией обратной связью
- •48. Такаги-Сугено модель оу в пространстве состояний
- •49. Нечеткие множества. Синглтоны и лингвистические переменные.
- •50. Моделирование нелинейных динамических оу с помощью нейронных сетей
- •51. Структура интеллектуальной системы управления
- •52. Многослойная нейронная сеть
- •53. Дефаззификация. Методы дефаззификации.
- •54. Нейронная сеть с радиальными базисными функциями
- •56. Синтез нечеткой обратной связи
- •57. Линейные матричные неравенства, основные понятия.
- •58. Аппроксимация функций (моделирование) с помощью нейронных сетей (персептронов)
- •59. Классификация генетических нечетких систем
- •60. Синтез нейронных нечетких сетей. Структура anfis
- •19. Моделирование статических объектов управления как аппроксимация функций с помощью нейронных сетей.
- •Адаптивные нейронные нечеткие системы интерференции (anfis). . Синтез нечетких нейронных сетей
- •5.1. Введение
- •Адаптивные нейронечеткие системы инференции (anfis)
- •Импликация Мамдани. Внешнее произведение. Таблица импликации.
- •Нечеткая идентификация. Структура и параметры
- •Нечеткий логический вывод для нескольких правил и нескольких входов.
- •1. Настройка пид-регулятора
- •3. Перенос параметров пид-регулятора в нечеткий контроллер
- •Анализ устойчивости тс модели объекта управления в пространстве состояний. Анализ устойчивости тс модели объекта
- •1. Настройка пид-регулятора
- •Нечеткий логический вывод (инференция). Пример.
- •Визуализация нечеткого логического вывода. Агрегирование условий и активизация заключений.
- •Математическая модель нейрона. Математическая модель нейрона
- •Нечеткое управление с предсказанием.
- •Визуализация нечеткого логического вывода. Аккумуляция заключений.
- •5.1. Введение
- •Алгоритм обучения anfis
- •Максиминная композиция нечетких отношений. Внутреннее произведение. Пример.
- •Преобразование вход-выход для нечетких контроллеров. Кривая управления и поверхность управления.
- •2.4. Преобразование вход-выход
- •Табличное изменениекоэффициентаусиления (супервизорное управление).
- •2.8. Табличное изменение коэффициента усиления (супервизорное управление)
- •Алгоритм нечеткой кластеризации Густафсона-Кесселя.
- •Генетические алгоритмы. Генетические алгоритмы
- •Модель Такаги-Сугено как квазилинейное (аффинное) устройство. Модель Такаги-Сугено как квазилинейное устройство
- •Контроллер типа Такаги-Сугено.
- •Деффазификация. Методы деффазификации.
- •2.2.5. Дефаззификация
- •Теорема б универсальной аппроксимации.
- •Такаги-Сугено модель объекта управления в пространстве состояний.
- •Табличный контроллер. Билинейная интерполяция.
- •2.3. Табличный контроллер
- •Моделирование нелинейных динамических объектов управления с помощью нейронных сетей.
- •Моделирование нелинейных динамических процессов (объектов)
- •Упрощение алгоритма нечеткого логического вывода.
- •Обратное распространение ошибки. Обновление весовых коэффициентов выходного слоя.
- •4.6. Обратное распространение ошибки
- •Структура интеллектуальной системы управления.
- •Многослойная нейронная сеть. Многослойная нейронная сеть
- •5.1. Введение
- •Структура anfis
Алгоритм нечеткой кластеризации Густафсона-Кесселя.
Генетические алгоритмы. Генетические алгоритмы
Проблема использования для обучения сети алгоритма обратного распространения ошибки и оптимизации по методу наименьших квадратов состоит в том, что их применение может быть причиной останова оптимизационного процесса в точках локального минимума нелинейной целевой функции (критерия качества сети). Дело в том, что упомянутые методы основаны на вычислениях производных. Генетические алгоритмы − естественный отбор самого подходящего (выживает наиболее приспособленный!) − не требуют вычисления производных и являются стохастическими оптимизационными методами, поэтому менее склонны к останову оптимизационного процесса в локальных минимумах. Эти алгоритмы могут быть использованы для оптимизации, как структуры, так и параметров в нейронных сетях. Специальная область их применения связана с определением параметров нечетких функций принадлежности.
Генетические алгоритмы имитируют эволюцию популяций. Суть этих алгоритмов такова. В начале генерируют возможные различные решения, используя генератор случайных чисел. Затем происходит тестирование (оценка) этих возможных решений с точки зрения поставленной задачи оптимизации, т.е. определяется, насколько хорошее решение они обеспечивают. После чего часть лучших решений отбирается, а другие отсеваются (выживает наиболее приспособленный). Затем отобранные решения подвергаются процессам репродукции (размножения), скрещивания и мутации, чтобы создать новую генерацию (поколение, потомство) возможных решений, которая, как ожидаемо, будет более подходящей, чем предыдущая генерация. Наконец, создание и оценивание новых генераций продолжатся до тех пор, пока последующие поколения не будут давать более подходящих решений. Такой алгоритм поиска решений из широкого спектра возможных решений оказывается предпочтительнее с точки зрения окончательных результатов, чем обычно используемые алгоритмы. Платой является большой объем вычислений. Рассмотрим составные части генетического алгоритма.
Кодирование. Множество параметров для задачи оптимизации кодируется в последовательность бит. Например, точка с координатами (x,y)=(11, 6) может быть представлена как хромосома, которая имеет вид соединения двух битовых последовательностей
-
1
0
1
1
0
1
1
0
Каждая координата представлена геном из четырех бит. Могут быть использованы другие методы кодирования и могут быть предусмотрены меры для кодирования отрицательных чисел и чисел с плавающей запятой.
2. Вычисление функции приспособленности (соответствия). После генерации популяции хромосом вычисляется значение функции приспособленности (соответствия) для каждой из ее хромосом. Функция приспособленности определяется через целевую функцию путем ее инвертирования (целевая функция минимизируется, а функция приспособленности максимизируется). Для задач максимизации значение функции приспособленности i-го члена вычисляется как величина, обратная целевой функции в i-ой точке. Обычно применяют строго положительную целевую функцию. Другая возможная мера приспособленности использовать ранжирование (классификацию) членов популяции. В этом случае целевая функция может быть вычислена не очень точно при условии, если она обеспечивает правильное ранжирование.
3. Селекция. Алгоритм селекции выбирает из членов популяции (хромосом), какие из них должны принять участие в качестве родителей с целью создания потомства для следующего поколения. Обычно вероятность отбора хромосом для этой цели пропорциональна присущей им величине приспособленности. Основная идея отбора состоит в том, членам с приспособленностью выше средней позволить размножаться и тем самым заменить члены с величиной приспособленности ниже средней.
4. Скрещивание. Операторы скрещивания генерируют новые хромосомы, которые, надеются, сохранят хорошие свойства от предыдущей генерации. Операция скрещивания обычно применяется к выбранной паре родителей с вероятностью, равной скорости скрещивания. При одноточечном скрещивании точка скрещивания в генетическом коде выбирается случайным образом, и две хромосомы-родители обмениваются своими последовательностями бит, расположенными справа от этой точки. Возьмем для примера две хромосомы
-
1
0
1
1
0
1
1
0
-
1
0
1
1
0
0
0
0
Если точка скрещивания расположена между пятым и шестым битами, цифры, написанные курсивом обмениваются местами по вертикали. Две новых хромосомы будут выглядеть так
-
1
0
1
1
0
0
0
0
-
1
0
1
1
0
1
1
0
При двухточечном скрещивании выбираются две точки скрещивания и части последовательностей хромосом, расположенные между двумя этими точками, обмениваются местами. В результате такого обмена получают двух детей от этих родителей. Фактически родители переносят фрагменты своих собственных хромосом на хромосомы своих детей. При этом такие дети, надеются, способны превосходить по приспособленности своих родителей, если они получили хорошие гены от обоих родителей.
Мутация. Оператор мутации может создать самопроизвольно новые хромосомы. Самый распространенный метод перебрасывать биты из одного места хромосомы в другое с весьма небольшой вероятностью, определяемой скоростью мутации. Мутация предотвращает сходимость популяции к локальному минимуму. Скорость мутации должна быть невысокой, чтобы не потерять хорошие гены. Мутация обеспечивает защиту от слишком раннего завершения алгоритма (в случае выравнивания всех хромосом и целевой функции).
Заметим, что выше было дано только лишь общее описание основных черт генетического алгоритма. Конкретные его детали весьма отличаются от описанных выше.
Алгоритм. Пример простого генетического алгоритма для задачи максимизации состоит из следующих этапов.
Инициализировать популяцию с генерируемыми случайным образом особями и вычислить значение функции приспособленности для каждой особи.
а) Отобрать из популяции два члена с вероятностью, пропорциональной их степени приспособленности.
б) Осуществить скрещивание со скоростью, равной скорости скрещивания.
в) Осуществить мутацию со скоростью, равной скорости мутации.
г) Повторять этапы с а) до г) до тех пор, пока число членов не будет достаточно, чтобы сформировать следующее поколение.
3. Повторять этапы 2 и 3 до тех пор, пока не будут удовлетворяться условия останова алгоритма.
Если скорость мутации высокая (выше 0,1), эффективность алгоритма будет такая же плохая, как в случае использования слепого случайного поиска.
Извлечение правил с помощью нечеткой кластеризации.
Нечеткий сумматор для контроллеров с двумя входами и одним выходом.
Нейросетевое прямое и косвенное адаптивное управление с эталонной моделью.
Обратное распространение ошибки. Обновление весовых коэффициентов скрытых слоев. Локальные градиенты.
4.6. Обратное распространение ошибки
Метод обратного распространения ошибки представляет собой популярную процедуру обучения многослойного персептрона. Он основан на дельта-правиле и использует критерий качества обучения (сумму квадратов ошибок ej=dj-yj)
(5)
для нейронов выходного слоя. Этот критерий есть сумма квадратов ошибок, получаемых на выходе каждого нейрона выходного слоя.
Весовой коэффициент передачи сигнала от p-го нейрона предыдущего слоя к q-му нейрону последующего слоя обновляется в соответствии с обобщенным дельта-правилом
. (6)
Чтобы обозначения были более понятными, мы опустили индекс обучающего образца k; очевидно, что уравнение (6) является рекуррентным, т.е. в его левой части представляет новое значение весового коэффициента, в то время как в правой части является прежним весом. Здесь - параметр скорости обучения. В обобщенном дельта-правиле корректировка весового коэффициента пропорциональна градиенту ошибки / , другими словами, чувствительности критерия качества к изменению весового коэффициента. Чтобы применить данный алгоритм, необходимы два цикла вычислений, прямое распространение и обратное распространение.
В прямом цикле вычислений веса остаются неизменными. Прямое распространение сигнала начинается в первом скрытом слое, ведя счет от входного слоя, путем подачи на его вход образцового входного векторного сигнала и заканчивается в выходном слое после вычисления сигнала ошибки (разности между образцовым выходным сигналом и выходным сигналом нейрона) для каждого нейрона выходного слоя. Обратное распространение сигнала начинается в выходном слое и продолжается путем распространения сигнала ошибки назад справа налево через всю сеть, слой за слоем.
Для описания алгоритма обратного распространения сигнала ошибки предположим, что j – й нейрон является нейроном выходного слоя (рис. 7). На рис. 7 показаны в явном виде связи между нейроном j выходного слоя, нейроном i скрытого слоя 1, нейроном r скрытого слоя 2 и нейроном s скрытого слоя 3.
Рис. 7
Заменяя в (6) q на j и p на i, получаем формулу для настройки весовых коэффициентов выходного слоя
. (6а)
Используя цепное правило дифференцирования, запишем производную, входящую в уравнение (6а), в виде
. (7)
Здесь с учетом
(5)
=
=
-
есть ошибка
j-го
нейрона,
есть выход j-го
нейрона,
![]() (4c)
есть внутренний
вход j-го
нейрона, полученный после суммирования
взвешенных выходов всех нейронов
предшествующего первого скрытого слоя,
в том числе выхода
i-го
нейрона этого слоя,
есть весовой
коэффициент
передачи сигнала от i-го
нейрона первого скрытого слоя к входу
j-го
нейрона выходного слоя. При этом
(4c)
есть внутренний
вход j-го
нейрона, полученный после суммирования
взвешенных выходов всех нейронов
предшествующего первого скрытого слоя,
в том числе выхода
i-го
нейрона этого слоя,
есть весовой
коэффициент
передачи сигнала от i-го
нейрона первого скрытого слоя к входу
j-го
нейрона выходного слоя. При этом
,
где - активационная функция. Как обозначена производная от функции по ее аргументу. С учетом (7) и (4c), находим
, (8)
где
. (8a)
Как видим, для обновления весовых коэффициентов выходного слоя надо найти ошибку , выход i-го первого скрытого слоя и производную .
Найдем формулу для обновления коэффициентов первого скрытого слоя
. (9)
Ошибка j-го нейрона связана с желаемым выходом и очевидно, что = - . Для i-го нейрона первого скрытого слоя в соответствии с методом обратного распространения ошибки мы должны использовать ошибку , т.к. она по аналогии с (7) должна входить в первые две частные производные для . Однако возникает проблема, обусловленная тем обстоятельством, что такая ошибка неизвестна для нейронов скрытого слоя. Чтобы преодолеть эту трудность, определим произведение упомянутых производных непосредственно
. (10)
Частная производная от по выходу i-го нейрона скрытого слоя, прямо связанная с выходом j-го нейрона выходного слоя, определяется как
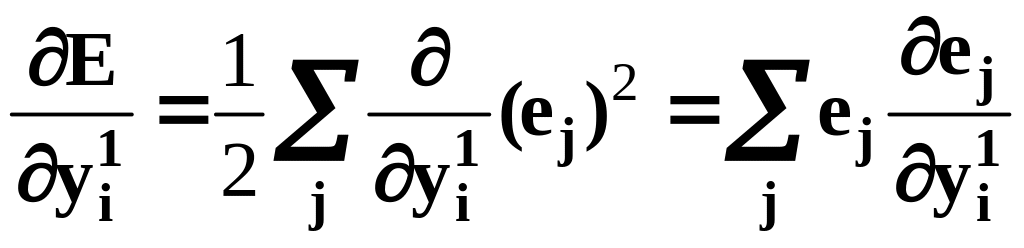 (11)
(11)
 (12)
(12)
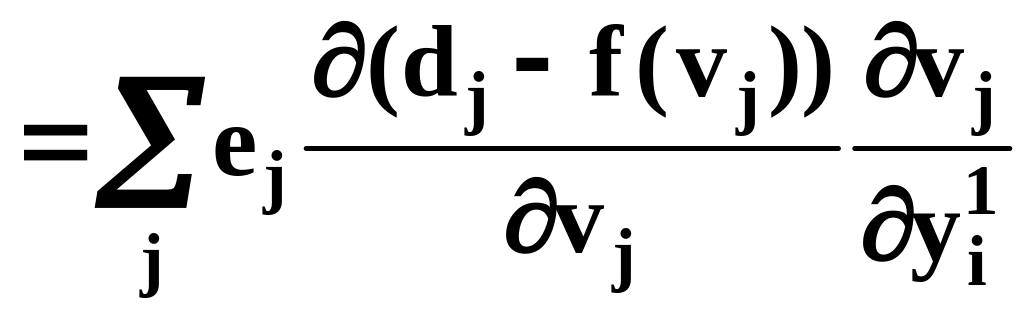 (13)
(13)
![]() .
(14)
.
(14)
Для получения последнего результата принято во внимание (4c).
Используя цепное правило дифференцирования с учетом (14) и
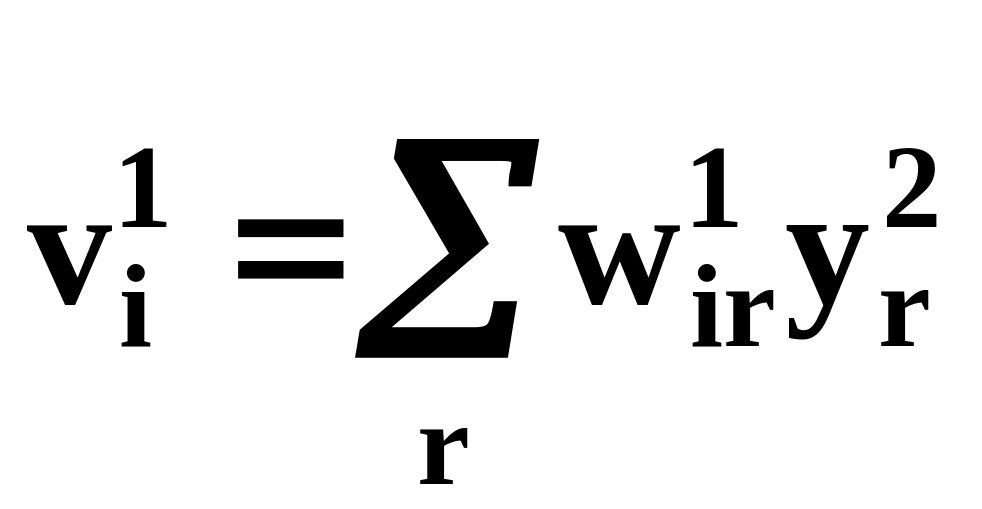 (17),
запишем производную
(17),
запишем производную
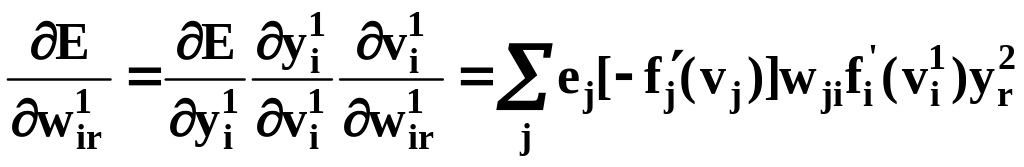 . (15)
. (15)
При этом c помощью дельта-правила (9) получаем формулу для обновление коэффициентов первого скрытого слоя
![]() ,
(16)
,
(16)
где
![]() .
(16а)
.
(16а)
Здесь i
– номер нейрона первого скрытого слоя,
r
– номер
нейрона второго скрытого слоя,
предшествующего первому скрытому слою,
j
– номер нейрона выходного слоя. Множитель
зависит лишь от
активационной функции
i
–го нейрона скрытого слоя и
.
Значения
содержат весовые
коэффициенты, связанные с нейронами
выходного слоя. Наконец,
есть выход
r
–го нейрона второго скрытого слоя и
этот выход появляется в выражении для
в результате
вычисления производной
![]() /
,
т.к. внутренний
вход i-го
нейрона
равен
/
,
т.к. внутренний
вход i-го
нейрона
равен
. (17)
Как видим, операция суммирования по j требует знания ошибок для всех нейронов выходного слоя. Это говорит о том, что как бы ошибка = - , имеющая место на выходе нейронной сети, «переместилась назад» с выходного слоя на первый скрытый слой.
Для s-го нейрона следующего второго скрытого слоя, предшествующего первому скрытому слою, правило обновления применяется рекуррентно по аналогии с (16) и (16а):
![]() .
(17а)
.
(17а)
Здесь ошибка = - фигурирует в и теперь имеет место перемещение этой ошибки с первого скрытого слоя на второй скрытый слой.
В общем, коррекция (обновление) весового коэффициента , связывающего вход p –го нейрона данного слоя с выходом q – го нейрона предшествующего слоя, определяется как
. (18)
Здесь - параметр скорости обучения, - называется локальным градиентом (сравните с (8), (16) и (17а)) и - входной сигнал q –го нейрона.
Локальный градиент вычисляется рекуррентно для каждого нейрона и его выражение зависит от того, где расположен нейрон в выходном или скрытом слое:
Если q – й нейрон принадлежит выходному слою, то согласно (8а)
. (19)
Оба сомножителя в произведении относятся к q –му нейрону.
Если q – й нейрон расположен в k–ом скрытом слое (рис. 8), то согласно (17а) при замене r на q , 2 на k, 1 на k-1 и i на r
![]() ,h,
(20)
,h,
(20)
где h – число скрытых слоев.
Как видим,
представляет собой
взвешенную сумму локальных градиентов
нейронов,
расположенных в (k-1)-ом
слое, непосредственно предшествующем
скрытому слою (считая справа налево),
причем
и вычисляется по
формуле (19), а
.
Так при k=1
![]() что
совпадает с (16а) при замене r
на j
и q
на i.
что
совпадает с (16а) при замене r
на j
и q
на i.
Рис. 8
Весовые коэффициенты связей, питающих выходной слой, обновляются за счет использования дельта-правила (18), в котором локальный градиент определяется по выражению (19). Вычислив для всех нейронов выходного слоя, мы затем используем (20), чтобы найти локальные градиенты для всех нейронов следующего слоя и изменить все весовые коэффициенты связей, питающих этот слой. Чтобы можно было вычислить для каждого нейрона, активационная функция всех нейронов должна быть дифференцируемой.
Алгоритм. Алгоритм обратного распространения включает пять шагов.
а) Инициализация весовых коэффициентов. Установите все весовые коэффициенты равными небольшим случайным числам.
б) Предъявление входов и соответствующих им желаемых выходов (обучающие пары). Подаем на нейросеть вектор входа u и соответствующий желаемый вектор выхода d. Вход может быть новым в каждой новой попытке обучения или образцы из обучающего множества могут подаваться на сеть циклически до тех пор, пока весовые коэффициенты не стабилизируются, т.е. перестанут изменяться.
в) Вычисление
действительных значений выхода.
Вычисляем вектор выхода последовательно
используя выражение
![]() ,
где f
есть вектор активационных функций.
,
где f
есть вектор активационных функций.
г) Настройка весовых коэффициентов. Начинаем настройку с весов выходного слоя и затем идем назад к первому скрытому слою. Весовые коэффициенты настраиваем с помощью
. (21)
В этом уравнении есть весовой коэффициент соединения, связывающего нейрон p скрытого слоя с нейроном q следующего слоя, - выход нейрона p (или внешний вход для нейрона q), есть параметр скорости обучения и - градиент. Если нейрон q является нейроном выходного слоя, то вычисляется с помощью (19) и если нейрон q является нейроном скрытого слоя, то определяется с помощью (20). Ускорение сходимости можно иногда обеспечить, если добавить значение момента.
Пример (локальный
градиент).
Логистическая (сигмоидная) функция
![]() дифференцируема, и ее производная
имеет вид
дифференцируема, и ее производная
имеет вид
![]() .
Мы можем
исключить экспоненту и записать
производную как
.
Мы можем
исключить экспоненту и записать
производную как
![]() . (22)
. (22)
Для нейрона j в выходном слое мы можем выразить локальный градиент как
![]() .
(23)
.
(23)
Для нейрона i скрытого слоя локальный градиент равен
![]() . (24)
. (24)
