57. Линейные матричные неравенства, основные понятия.

58. Аппроксимация функций (моделирование) с помощью нейронных сетей (персептронов)

Рассмотрим задачу реализации нелинейных алгебраических зависимостей нейронными сетями. Приведенный выше персептрон может аппроксимировать произвольную гладкую функцию. В качестве примера запишем выходной сигнал сети с одним выходом y и одним входом u, состоящей из одного скрытого слоя с двумя нелинейными нейронами и выходного слоя из одного линейного нейрона (с линейной активационной функцией) . (28). Внутренние входы v₁ и v₂ скрытых нейронов определяются выражениями . (29). Пусть функция активации f (v) скрытых нейронов является функцией tangh(v) (гиперболический тангенс). При этом график зависимости y=g(u) при найденных в результате обучения значениях весовых коэффициентов w⁰ , w^h и смещений b^h можно построить, как показано на рис. 8. Здесь = , = - , = =1.

Рис. 8

Изменяя веса и смещения в соответствии с обучающей выборкой,

получаем гладкую кривую, аппроксимирующую вход нейронной сети.

Эффективность использования нейронных сетей устанавливается

теоремой о полноте. Смысл этой теоремы в том (Cybenko, 1989), что

персептрон, по меньшей мере, с одним скрытым слоем, способен

аппроксимировать любую непрерывную функцию с

произвольной степенью точности при условии выбора достаточного числа

нейронов скрытого слоя.

59. Классификация генетических нечетких систем

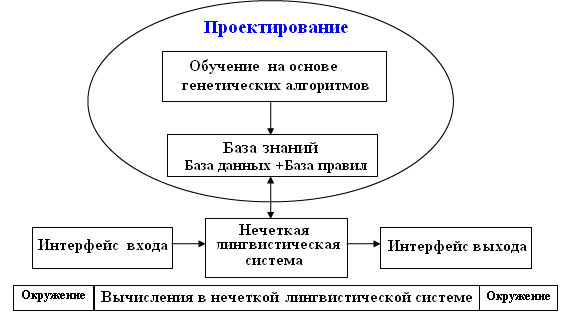
Нечеткие системы успешно применяются в задачах моделирования и управления, и в значительном числе приложений. В большинстве случаев ключом для успешного применения служит способность нечетких систем встраивать знания экспертов.

Появилось 2 подхода к изучению нечетких систем, дополненных способностями к обучению:

1. гибридизация, осуществленная в рамках мягких вычислений с помощью других технологий, таких как, нейронные сети и эволюционные вычисления, которые придают нечетким системам способность к обучению (рис. 5). Нейро-нечеткие системы являются одним из самых успешных и очевидных направлений этих усилий.

2. генетические нечеткие системы (ГНС).

ГНС в сущности представляет собой нечеткую систему, расширенную за счет процесса обучения, основанного на генетическом алгоритме (ГА). Самыми заметными приложениями ГНС являются генетические нечеткие лингвистические системы (ГНЛС), в которых генетический процесс обучает или настраивает различные компоненты нечетких лингвистических систем, т.е. систем построенных исключительно с помощью правил в отличие от нечетких систем Такаги-Сугено.

Недостатки проектирования нечетких лингвистических систем с помощью экспертов:

• Не всегда можно найти сведущего эксперта;

• Извлечение знаний из эксперта отнимает много времени;

• Системы, построенные на приобретенных с помощью эксперта знаниях, работают плохо.

Присущая ГА гибкость и способность встраивать полученные от экспертов знания являются весьма важным свойством с точки зрения решаемых задач. Другие подходы включают генетические нейронечеткие системы и генетическую нечеткую кластеризацию.

Проектирование нечетких систем

Нечеткие системы включают два главных компонента:

• 1.Базу знаний (БЗ), в которой хранятся доступные или приобретенные знания о задаче, требующей решения, в форме нечетких правил;

2.Механизм инференции, использующий методы нечетких рассуждений, базирующиеся на базе правил и входных сигналах, для получения выходного сигнала системы.

Оба этих компонента должны быть спроектированы так, чтобы построить систему для конкретного приложения:

• БЗ формируют из знаний экспертов или путем обучения с помощью машинных методов;

• Механизм инференции строят путем выбора нечетких операторов для каждого компонента (конъюнкция, импликация, дефаззификация и т.п.).

В ряде случаев операторы также параметризуются и могут быть настроены автоматическими методами.

Проектирование БЗ затрагивает две подзадачи:

1. Определение базы данных (БД):

• Универсум для переменных;

• Масштабирующие коэффициенты или функции;

• Число лингвистических терм для каждой переменной;

• Функции принадлежности, описывающие термы.

2. Составление базы правил (БП): формулировка базовых правил. Как уже отмечено, существуют два различных метода для проектирования базы знаний (БЗ): информация от экспертов и с помощью нечеткого моделирования.

Классификация генетических нечетких систем

Первый шаг в проектировании ГНЛС решить вопрос о том, какая часть нечеткой системы подлежит оптимизации путем кодирования ее параметров в хромосомы. В этом разделе мы представим классификацию ГНЛС, соответствующую различным частям нечеткой системы, кодируемым с помощью генетической модели. Обычно методы проектирования ГНЛС разделяют на два процесса, настройка (т.е. адаптация) и обучение.

• Генетическая настройка. Если существует БЗ, мы применяем процесс генетической настройки для улучшения свойств нечеткой системы, но не изменяем БП. Т.е. мы настраиваем параметры НЛС с целью улучшения ее свойств, сохраняя неизменной БП.

• Генетическое обучение. Вторая возможность обучать компоненты БП, к которым можно отнести адаптацию механизма инференции. Т.е. мы затрагиваем обучение компонентов БП, наряду с другими компонентами НЛС.

1. Г 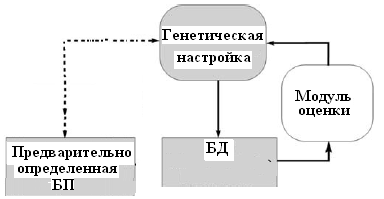енетическая настройка базы знаний. Осуществляется путем определения предварительно вида и параметров масштабирующих функций входа и выхода, а также функций принадлежности, и затем настройки этих параметров и тем самым изменения формы масштабирующих функций и функций принадлежности с помощью ГА (рис. справа).

2. Генетическое обучение базы правил. Генетическое обучение БП предполагает предопределенное множество функций принадлежности в БД, к которым правила обращается посредством лингвистических терм.

Имеется три главных подхода: питтсбургский, мичиганский и итеративный методы обучения. Питтсбургский «хромосома=набор правил», сохраняя неизменной популяцию кандидатов на роль правил и, используя селекцию, и генетические операторы для создания новых поколений наборов правил. Мичиганский «хромосома=правило» и набор правил представляется всей популяцией. В третьем случае, итеративном методе с помощью хромосом кодируют отдельные правила, и новое правило настраивается и добавляется в набор правил, итеративным способом.