53. Дефаззификация. Методы дефаззификации.

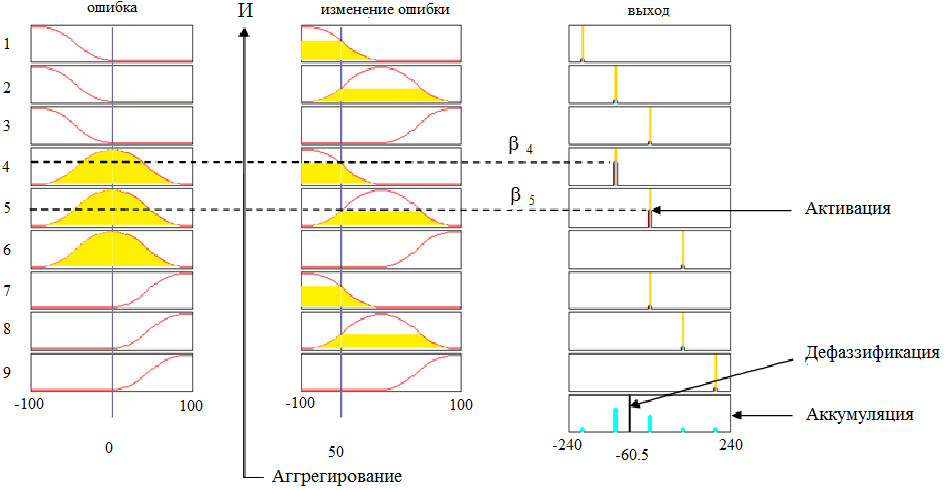Результирующее нечеткое множество выхода, определяемое функцией принадлежности, показанной на рис. 2.8 (внизу справа) и на рис. 2.10 (крайнее справа), должно быть преобразовано в четкое число (другими словами, качественная информация должна быть преобразована в количественную), которое может быть использовано как физическое значение управляющего сигнала. Такая операция называется дефаззификацией и на рис. 2.10 абсцисса точки, определяющей позицию белой разделительной линии, дает значение управляющего сигнала u = -35,9. Таким образом, результирующее нечеткое множество выхода «дефаззифицируется» в четкий управляющий сигнал.Существуют несколько методов дефаззификации. Центр тяжести (COG). В этом методе четкий выходной сигнал (белая линия на рис. 2.10) есть абсцисса центра тяжести функции принадлежности результирующего нечеткого множества выхода

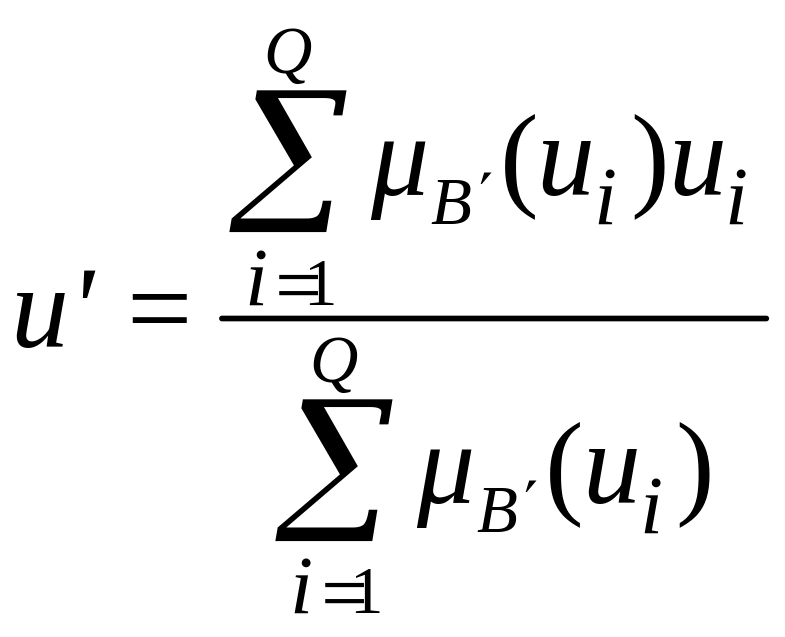, (2.33),где − текущая точка в дискретном универсуме, − соответствующее значение степени принадлежности, Q – число элементов в дискретном универсуме для управляющего сигнала. Выражение можно интерпретировать как взвешенное среднее значение элементов в опорном множестве. Разумеется, перед использованием формулы (2.33) надо осуществить дискретизацию . Для непрерывного случая суммирование заменяется интегрированием 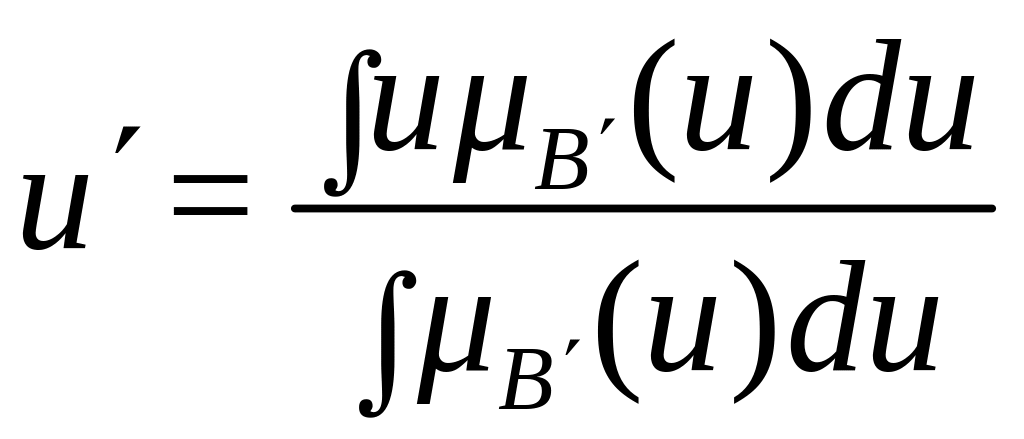. (2.34). Здесь − функция принадлежности нечеткого множества выхода после операции аккумуляции. Этот метод является весьма полезным методом. Однако его вычислительная сложность, особенно применительно к (2.34), относительна велика. Его также называют центроид площади.Метод центра тяжести для синглтонов (одноточечных множеств)(COGS)

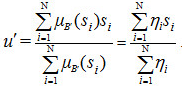Специальный случай лингвистической модели получается, когда нечеткие множества B_i заключений (выхода), в данном случае управляющего сигнала являются синглтонами (одноточечными множествами). Такие множества представляют собой просто вещественные числа s_i , что приводит к следующим правилам Если x₁ есть A_1i и x₂ есть A_2i и … x_r есть A_ri , то u есть s_i, .Эта модель называется синглтонной моделью. Более простая версия формулы (2.33) (метод нечетких средних) обычно используется для определения четкого выхода такой модели:

(2.35). Здесь позиция i-го синглтона в универсуме выхода, равно возбуждающей силе i-го синглтона, N- число правил. По формуле (2.35) для рассмотренного в на рис. 2.8 примера было вычислено четкое значение управляющего сигнала, равное -60,5. Оно представлено синглтоном в виде тонкой вертикальной линии на рис. 2.8 (крайний нижний ряд справа).Этот метод дефаззификации относительно предпочтителен с точки зрения вычислительной сложности и к тому же u’ − функция, дифференцируемая в отношении синглтонов , что благоприятно с точки зрения его (метода) использования в нейронечетких системах (см. ниже). Заметим, что синглтонная нечеткая модель принадлежит к общему классу аппроксимирующих функций (аппроксиматоров), называемых разложением на базисные функции и имеющих вид . Большинство структур, используемых для идентификации нелинейных систем, таких, как искусственные нейронные сети, нейронные сети с радиальными базисными функциями или сплайны принадлежат к этому классу аппроксиматоров. В синглтонной модели для r входов базисными функциями являются нормализованные степени истинности (возбуждающие силы) правил ,

и постоянными являются заключения (синглтоны) правил.