2. Алгоритм жесткой кластеризации.

Жесткий алгоритм с-средних (HCM) пытается (старается) локализовать кластеры в многомерном пространстве признаков. Цель алгоритма приписать (отнести) каждую точку данных в пространстве признаков к конкретному кластеру. Сущность данного метода заключается в следующем. Предполагается, что число кластеров известно, или, в крайнем случае, фиксировано, т.е. предполагается, что алгоритм будет разделять предъявленное множество данных X ={x₁ ,…,x_n} (n –число признаков) на с кластеров, где с - известное число. Таким образом, этот алгоритм принадлежит к числу супервизорных алгоритмов. Каждый из кластеров характеризуется своим прототипом (прообразом центра кластера) v_i . Эти прототипы вначале выбираются случайным образом. Затем каждый вектор данных приписывается к ближайшему прототипу (с использованием евклидова расстояния). Затем каждый прототип заменяется средним значением тех данных, которые приписаны к этому кластеру. Альтернирующее (чередующееся) приписывание данных к ближайшему прототипу и обновление прототипов, другими словами, центров кластеров повторяется, пока не произойдет сходимость алгоритма, т.е. пока не перестанут изменяться значения прототипов. Некоторые дополнительные правила могут быть введены в рассмотрение, чтобы избежать необходимости точного знания числа кластеров. Эти правила позволяют объединить ближайшие (соседние) кластеры в один кластер, а кластеры, которым соответствуют большие среднеквадратические отклонения координат, разбить на два и более кластеров.

Пример 4 (два кластера). Рассмотрим данные, представленные в виде точек

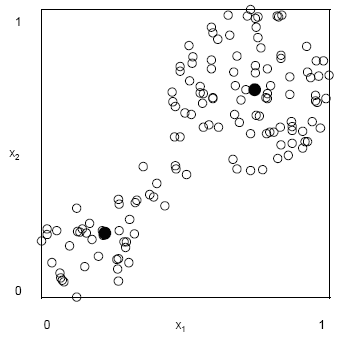на рис. 5. Алгоритм кластеризации находит один центр в нижнем левом углу и другой в правом верхнем углу (центры кластеров представлены черными жирными кружками). Начальное расположение центров (прототипов) примерно соответствовало средней части рисунка, и в процессе итераций они (центры) перемещались к своим конечным позициям. Заметим, что каждая точка данных принадлежит лишь тому или другому кластеру, так что кластеры являются четкими. В общем, признаки данных должны быть нормализованы для того, чтобы измерение расстояния осуществлялось надлежащим образом (правильно).

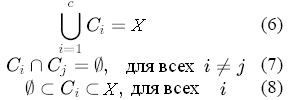В сущности, жесткий алгоритм с-средних значений основан на с-разделении пространства данных X на подмножества кластеров {C_i}, i=1,2,…,c. При этом используются следующие теоретико-множественные соотношения(6,7,8)

Множество X ={x₁ ,…, x_n} является конечным множеством в пространстве, образованном признаками, и с – число кластеров.Заметим,что , ( 9) ибо если c=K , то каждый вектор данных является кластером, и если с=1, то все данные принадлежат одному кластеру. Уравнения (6 - 8) выражают соответственно, что множество кластеров заполняет весь универсум, что ни один кластер не перекрывается с другими, и что каждый кластер не является пустым множеством и в то же время не содержит все предъявленные данные. Формально, алгоритм с - средних значений находит центры каждого кластера путем минимизации целевой функции, включающей меру расстояния. Этот алгоритм можно трактовать как стратегию для минимизации следующей целевой функции:

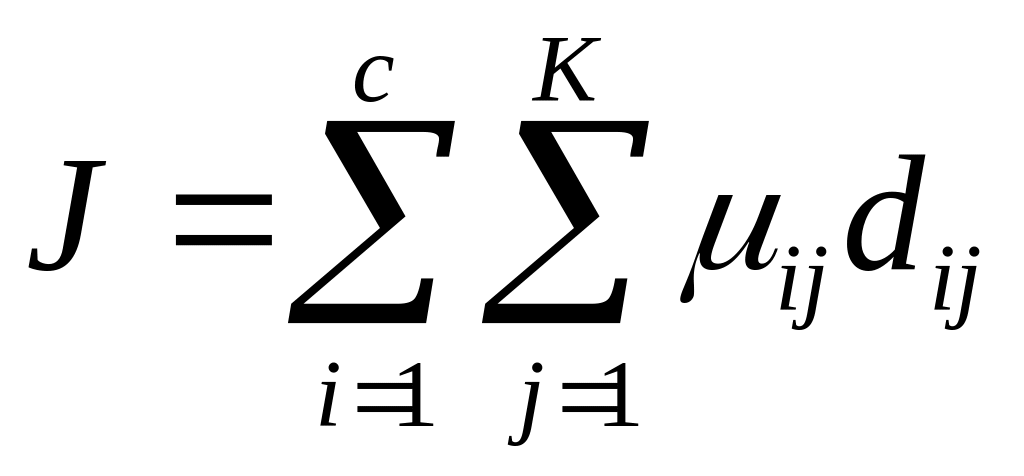(10) при условии 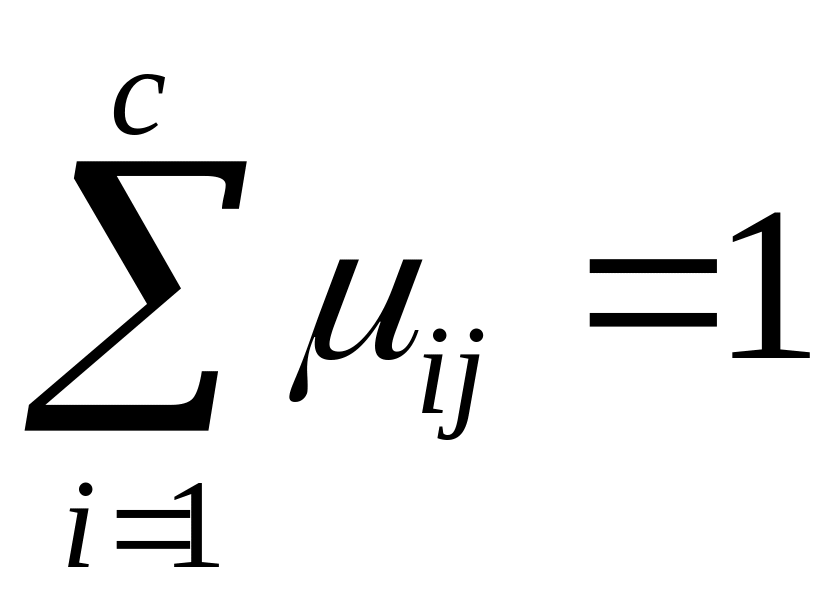для всех j=0, 1,…, K, (11), где величина определяет, приписан ли вектор данных x_j к кластеру i ( =1) или нет ( =0). Здесь есть квадрат евклидова расстояния от вектора данных до кластерного прототипа .

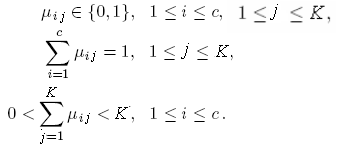Так как эта задача минимизации является нетривиальной нелинейной задачей условной минимизации с непрерывными и дискретными параметрами , то вышеупомянутый алгоритм, альтернативно оптимизирующий одно множество параметров, в то время как другое множество параметров считается фиксированным, кажется весьма разумным подходом для минимизации функции (10). При этом если кластерные центры фиксированы, то значения , которые минимизируют целевую функцию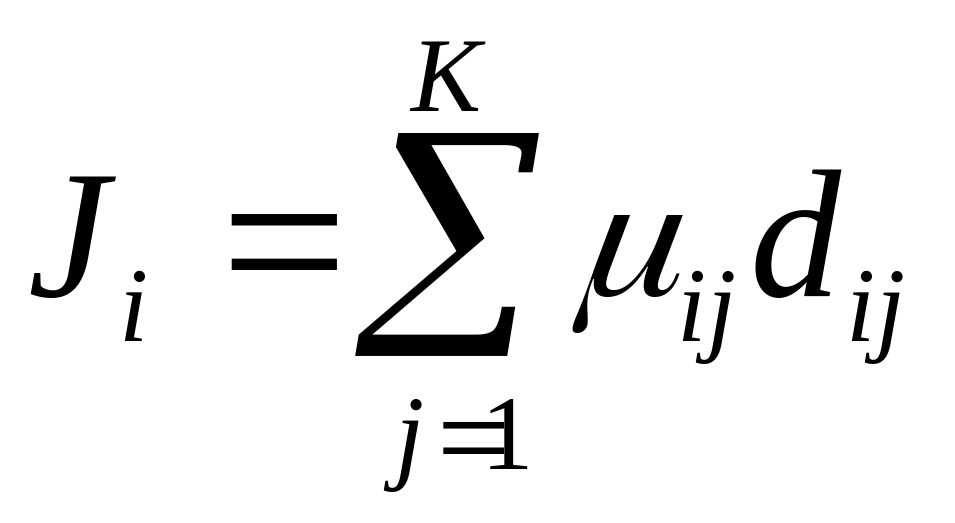 ,соответствующую кластеру с номером i, могут быть найдены как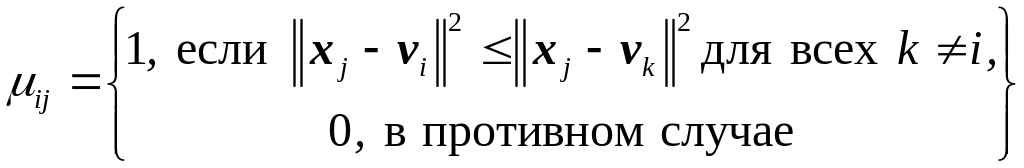 (12)

То есть, принадлежит кластеру i, если является ближайшим к нему центром по сравнению с другими центрами. Если с другой стороны значения зафиксированы, то оптимальные центры, минимизирующие (10), представляют собой средние значения всех векторов кластера i:

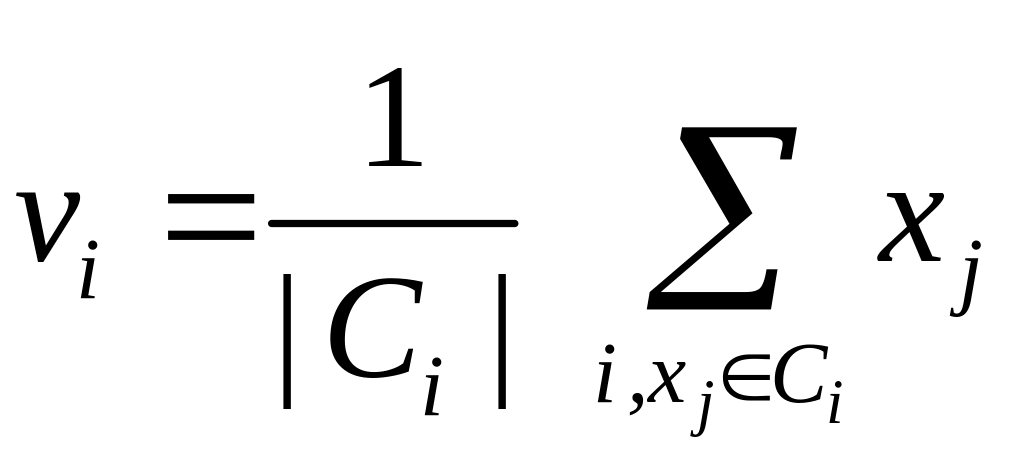, i=1,2,…,c . (13). Здесь есть число элементов (точек данных) во множестве , другими словами мощность этого множества, и сумма образуется поэлементным суммированием векторов.

Алгоритм. Жесткий алгоритм с - средних значений состоит из пяти шагов.

1.Определить начальные значения центров кластеров , i=1,2,…,c. Эта операция обычно выполняется путем случайного выбора c точек из точек данных.

2.Найти для всех i=1,2,…, c и j=1,…, K, используя (12).

3.Вычислить значение целевой функции (10). Прекратить дальнейшие вычисления, если значение целевой функции меньше допустимого значения или если ее изменения по сравнению со значением, полученным на предыдущей итерации, меньше заданного допуска.

4.Вычислить новые значения кластерных центров, применяя (13).

5.Перейти к шагу 2.

Алгоритм является итерационным, и нет гарантии, что он приведет к оптимальному решению. Окончательный результат зависит от выбранного на первом шаге начального положения центров кластеров, и поэтому рекомендуется использовать какие-нибудь методы для поиска хорошего начального расположения центров кластеров. Также можно начать вычисления с выбора случайным образом значений для всех i=1,2,…,c и j=1,…, K, и затем следовать по пути аналогичному рассмотренной выше итерационной процедуры.

Пример 5 (правила). Графическое представление данных на рис. 5 наводит на мысль о существовании связи между переменной x₁ на горизонтальной оси и переменной x₂ на вертикальной оси. Например, кластер в верхнем углу справа на этом рисунке говорит о том, в широком смысле, что если переменная x₁ является ‘большой’, т.е. принимает значения, близкие к правой границе горизонтальной оси, то переменная x₂ также является ‘большой’, т.е. принимает значения, близкие к верхней границе вертикальной оси. Эту связь можно описать с помощью правила, Если x₁ есть большая, то x₂ есть больша (14)Во всяком случае, интуитивно кажется возможным дать такую смысловую трактовку двум примерам слова ‘большая’, фигурирующих в правиле, анализируя расположение центра кластера. Кластер в левой нижней части рисунка можно, по-видимому, описать с помощью правилаь Если x₁ есть малая, то x₂ есть малая. (15)

Снова строгость последнего правила зависит от трактовки двух слов ‘малая’.