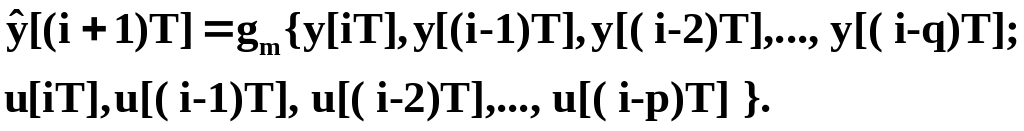- •1.Коньюнкция условий и разбиение пространства входа.
- •Композиция нечетких отношений.
- •Нечеткое инверсное управление и нечеткая система управления с внутренней моделью
- •Алгоритм жесткой кластеризации.
- •Операции над нечеткими множествами. Модификаторы.
- •8. Проектирование нечетких контроллеров (метод Мамдани)
- •2. Нечеткий контроллер с двумя входами и одним выходом
- •9.Нечеткая система управления с плановым изменением коэффициента.
- •10. Оценка параметров заключений по (мнк)
- •11. Адаптивные нейронные нечеткие системы инференции (anfis)
- •12.Импликация Мамдани. Внешнее произведение.Таблица импликаци
- •13. Нечеткая идентификация. Структура и параметры.
- •14. Нечеткий логический вывод для нескольких правил и нескольких входов.
- •Несколько входов (многомерная лингвистическая модель)
- •16. Функциональная схема нечеткого контроллера
- •17. Отношения между нечеткими множествами
- •18. Алгоритм нечеткой кластеризации с-средних
- •19. Моделирование статических объектов упр-я как аппроксимация функций с помощью нейронных сетей (есть только для динамических объектов)((((((((
- •20. Анализ устойчивости тс модели объекта управления в пространстве состояний.
- •22. Нечеткий логический вывод с исп-м отношений. Пример
- •24. Визуализация алгоритма нечеткого логического вывода.
- •25. Понятия о нечетких множествах
- •26. Обучение нейронной сети. Общие сведения.
- •27. Упрощение алгоритма нечеткого логического вывода.
- •28. Обратное распространение ошибки
- •29. Визуализация нечеткого логического вывода.Аккумуляция.
- •30. Параметры алгоритма с-средних
- •31. Проектирование нечетких контроллеров (метод Мамдани)
- •32. Нечеткая логика. Логические связки.
- •33.Проектирование нечетких контроллеров(метод Мамдани). Многомерный нечеткий контроллер.
- •34. Алгоритм обучения anfis
- •35. Максиминная композиция нечетких отношений. Внутренне произведение. Пример.
- •36. Преобразование вход-выход. Кривая управления. Пов-ть управления.
- •37. Табличное изменение коэффициента усиления (супервизорное управление)
- •38. Алгоритм нечеткой кластеризации Густафсона–Кесселя.
- •39. Генетические алгоритмы
- •40. Извлечение правил с помощью кластеризации
- •41.Нечеткий сумматор для контроллеров с 2 входами и 1 выходом
- •42. Нейросетевое прямое и косвенное адаптивное управление с эталонной моделью
- •43. Обратное распространение ошибки. Обновление весовых коэф-в скрытых слоев. Локальные градиенты.
- •44. Модель Такаги-Сугено как квазилинейное устройство
- •45. Контроллер типа Такаги-Сугено
- •46. Нейросетевое управление с адаптивной линеаризацией обратной связью
- •48. Такаги-Сугено модель оу в пространстве состояний
- •49. Нечеткие множества. Синглтоны и лингвистические переменные.
- •50. Моделирование нелинейных динамических оу с помощью нейронных сетей
- •51. Структура интеллектуальной системы управления
- •52. Многослойная нейронная сеть
- •53. Дефаззификация. Методы дефаззификации.
- •54. Нейронная сеть с радиальными базисными функциями
- •56. Синтез нечеткой обратной связи
- •57. Линейные матричные неравенства, основные понятия.
- •58. Аппроксимация функций (моделирование) с помощью нейронных сетей (персептронов)
- •59. Классификация генетических нечетких систем
- •60. Синтез нейронных нечетких сетей. Структура anfis
- •19. Моделирование статических объектов управления как аппроксимация функций с помощью нейронных сетей.
- •Адаптивные нейронные нечеткие системы интерференции (anfis). . Синтез нечетких нейронных сетей
- •5.1. Введение
- •Адаптивные нейронечеткие системы инференции (anfis)
- •Импликация Мамдани. Внешнее произведение. Таблица импликации.
- •Нечеткая идентификация. Структура и параметры
- •Нечеткий логический вывод для нескольких правил и нескольких входов.
- •1. Настройка пид-регулятора
- •3. Перенос параметров пид-регулятора в нечеткий контроллер
- •Анализ устойчивости тс модели объекта управления в пространстве состояний. Анализ устойчивости тс модели объекта
- •1. Настройка пид-регулятора
- •Нечеткий логический вывод (инференция). Пример.
- •Визуализация нечеткого логического вывода. Агрегирование условий и активизация заключений.
- •Математическая модель нейрона. Математическая модель нейрона
- •Нечеткое управление с предсказанием.
- •Визуализация нечеткого логического вывода. Аккумуляция заключений.
- •5.1. Введение
- •Алгоритм обучения anfis
- •Максиминная композиция нечетких отношений. Внутреннее произведение. Пример.
- •Преобразование вход-выход для нечетких контроллеров. Кривая управления и поверхность управления.
- •2.4. Преобразование вход-выход
- •Табличное изменениекоэффициентаусиления (супервизорное управление).
- •2.8. Табличное изменение коэффициента усиления (супервизорное управление)
- •Алгоритм нечеткой кластеризации Густафсона-Кесселя.
- •Генетические алгоритмы. Генетические алгоритмы
- •Модель Такаги-Сугено как квазилинейное (аффинное) устройство. Модель Такаги-Сугено как квазилинейное устройство
- •Контроллер типа Такаги-Сугено.
- •Деффазификация. Методы деффазификации.
- •2.2.5. Дефаззификация
- •Теорема б универсальной аппроксимации.
- •Такаги-Сугено модель объекта управления в пространстве состояний.
- •Табличный контроллер. Билинейная интерполяция.
- •2.3. Табличный контроллер
- •Моделирование нелинейных динамических объектов управления с помощью нейронных сетей.
- •Моделирование нелинейных динамических процессов (объектов)
- •Упрощение алгоритма нечеткого логического вывода.
- •Обратное распространение ошибки. Обновление весовых коэффициентов выходного слоя.
- •4.6. Обратное распространение ошибки
- •Структура интеллектуальной системы управления.
- •Многослойная нейронная сеть. Многослойная нейронная сеть
- •5.1. Введение
- •Структура anfis
50. Моделирование нелинейных динамических оу с помощью нейронных сетей
С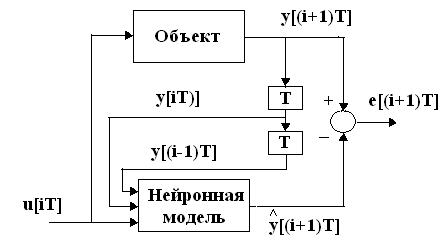
 пособность
нейронных сетей осуществлять нелинейное
преобразование сигналов может быть
использовано для моделирования
нелинейных динамических объектов. В
этом случае модель находится путем
обучения нейронной сети, т.е. путем
настройки весов так, чтобы минимизировать
ошибку моделирования. Использование
нейронных сетей для моделирования
поясним на примере дискретного
динамического нелинейного объекта с
одним входом и одним выходом. Предположим,
что на вход такого объекта поступает
управляющая последовательность u[iT]
, а на выходе с помощью датчика измеряется
управляемая последовательность y[iT].
Пусть известно, что дискретная модель
объекта является моделью второго
порядка. Заметим, что выбор порядка
модели относится к проблемам
идентификации нелинейных систем, но
не является предметом данного курса
лекций. Тогда общее описание нейронной
динамической модели с тремя входными
и одним выходным сигналом можно выразить
в форме
пособность
нейронных сетей осуществлять нелинейное
преобразование сигналов может быть
использовано для моделирования
нелинейных динамических объектов. В
этом случае модель находится путем
обучения нейронной сети, т.е. путем
настройки весов так, чтобы минимизировать
ошибку моделирования. Использование
нейронных сетей для моделирования
поясним на примере дискретного
динамического нелинейного объекта с
одним входом и одним выходом. Предположим,
что на вход такого объекта поступает
управляющая последовательность u[iT]
, а на выходе с помощью датчика измеряется
управляемая последовательность y[iT].
Пусть известно, что дискретная модель
объекта является моделью второго
порядка. Заметим, что выбор порядка
модели относится к проблемам
идентификации нелинейных систем, но
не является предметом данного курса
лекций. Тогда общее описание нейронной
динамической модели с тремя входными
и одним выходным сигналом можно выразить
в форме
![]() (30).
В этом уравнении
(30).
В этом уравнении
![]() обозначает реакцию нелинейного объекта
в момент t=(i
обозначает реакцию нелинейного объекта
в момент t=(i![]() 1)T,
а
1)T,
а
![]() - реакцию нейронной динамической модели
этого объекта в тот же момент времени
t=(i
+1)T на один и тот
же сигнал u[iT].
Для сравнения линейный аналог этой
нейронной модели описывается как
- реакцию нейронной динамической модели
этого объекта в тот же момент времени
t=(i
+1)T на один и тот
же сигнал u[iT].
Для сравнения линейный аналог этой
нейронной модели описывается как
![]() (31) с параметрами a1,
a2,
b1 ,
подлежащими оценке, и называется
авторегрессионной моделью (ARX-моделью).
Разностный сигнал e[(i+1)T]=
(31) с параметрами a1,
a2,
b1 ,
подлежащими оценке, и называется
авторегрессионной моделью (ARX-моделью).
Разностный сигнал e[(i+1)T]=
![]() -
-![]() управляет
процессом настройки весов нейронной
модели. Проблема идентификации объекта
сводится к построению такой его
параметрической нейронной модели, чтобы
реакции объекта y[i]
и модели
управляет
процессом настройки весов нейронной
модели. Проблема идентификации объекта
сводится к построению такой его
параметрической нейронной модели, чтобы
реакции объекта y[i]
и модели
![]() на
один и тот же управляющий сигнал u[i]
совпадали в пределах допустимой
ошибки
на
один и тот же управляющий сигнал u[i]
совпадали в пределах допустимой
ошибки
![]() ,
т.е.|
,
т.е.|
![]() -
|
-
|
![]() .
В случае применения для моделирования
объектов нейронная сеть обычно
подключается параллельно объекту и
использует для предсказания выхода
объекта смещенные в сторону запаздывания
выходные последовательности объекта
так, как это показано на рис. 9.При таком
подключении реакция сети зависит от
входа u[(iT)]
, а также от сигналов u1[iT]
=y[iT]
и u2[iT]=
y[(i-1)T],
представляющих собой две прошедшие
через линии задержки T
реакции желаемого сигнала, составляющих
ожидаемый выходной вектор сети. В этой
ситуации нейронная сеть выполняет
функции классической многослойной
статической сети. Найденная нейронная
модель тестируется с помощью свободного
запуска («free run»)
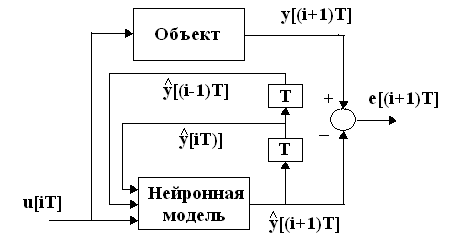
(рис. 11). Термин свободный запуск
используется, чтобы подчеркнуть контраст
с так называемым предсказанием на один
период дискретизации («one-step-
ahead prediction»)
(рис.10). При свободном запуске оценки
выходов объекта
.
В случае применения для моделирования
объектов нейронная сеть обычно
подключается параллельно объекту и
использует для предсказания выхода
объекта смещенные в сторону запаздывания
выходные последовательности объекта
так, как это показано на рис. 9.При таком
подключении реакция сети зависит от
входа u[(iT)]
, а также от сигналов u1[iT]
=y[iT]
и u2[iT]=
y[(i-1)T],
представляющих собой две прошедшие
через линии задержки T
реакции желаемого сигнала, составляющих
ожидаемый выходной вектор сети. В этой
ситуации нейронная сеть выполняет
функции классической многослойной
статической сети. Найденная нейронная
модель тестируется с помощью свободного
запуска («free run»)
(рис. 11). Термин свободный запуск
используется, чтобы подчеркнуть контраст
с так называемым предсказанием на один
период дискретизации («one-step-
ahead prediction»)
(рис.10). При свободном запуске оценки
выходов объекта
![]() и
и
![]() используются
как входы нейронной сети вместо измеренных
значений. Таким путем модель может быть
использована, чтобы моделировать объект
независимо от измеренных значений
выхода. Если модель используется для
предсказания на несколько периодов
дискретизации (на некоторый горизонт),
как это необходимо при управлении с
предсказанием, свободный запуск
представляет собой более дискриминационный
тест и более удобен для тестирования
модели, чем модель тестирования,
опирающаяся на предсказание на один
период дискретизации. В общем случае
для объектов высокого порядка в качестве
входов нейронной модели используют,
кроме настоящих значений входа u[iT]
и выхода y[iT],
p прошлых значений
входа u[(i-1)T],
u[(i-2)T],…,
u[(i-p)T],
и q прошлых
значений выхода y[(i-1)T],
y[(i-2)T],…,
y[(i-q)T],
так что общее описание нейронной
динамической модели можно представить
в виде
используются
как входы нейронной сети вместо измеренных
значений. Таким путем модель может быть
использована, чтобы моделировать объект
независимо от измеренных значений
выхода. Если модель используется для
предсказания на несколько периодов
дискретизации (на некоторый горизонт),
как это необходимо при управлении с
предсказанием, свободный запуск
представляет собой более дискриминационный
тест и более удобен для тестирования
модели, чем модель тестирования,
опирающаяся на предсказание на один
период дискретизации. В общем случае
для объектов высокого порядка в качестве
входов нейронной модели используют,
кроме настоящих значений входа u[iT]
и выхода y[iT],
p прошлых значений
входа u[(i-1)T],
u[(i-2)T],…,
u[(i-p)T],
и q прошлых
значений выхода y[(i-1)T],
y[(i-2)T],…,
y[(i-q)T],
так что общее описание нейронной
динамической модели можно представить
в виде