38. Алгоритм нечеткой кластеризации Густафсона–Кесселя.

В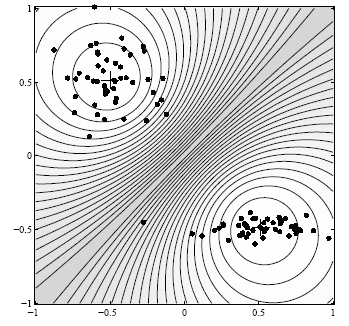 классическом алгоритме с-cредних расстояние между вектором x_j и центром ν_i кластера определяется, как евклидова норма (20). Определённое таким образом расстояние учитывалось в формуле (16), характеризующей значение целевой функции. При подобном задании меры расстояния между двумя векторами множество точек, равноудалённых от центра кластера, (контурных линий) принимает форму окружности с одинаковым масштабом по всем координатам (рис. 8). Если входные данные образуют группы, форма которых отличается от окружности, либо если шкалы значений отдельных координат вектора сильно различаются, рассчитанные значения не будут адекватно отражать принадлежность векторов x конкретным кластерам. В такой ситуации качество группирования можно существенно повысить за счет применения усовершенствованной версии алгоритма кластеризации, называемой алгоритмом Густафсона – Кесселя( ГК-алгоритм). Густафсон и Кессель расширили стандартный алгоритм нечетких с-средних путем использования адаптивной нормы расстояния для того, чтобы обнаруживать кластеры различной геометрической формы в одном и том же множестве данных. По отношению к алгоритму c-средних главное изменение состоит в том, каждый кластер имеет свою собственную нормо-индуцирующую матрицу А_i. При этом масштабированное расстояние между вектором x_j и центром ν_i определяется как норма внутреннего произведения (21). Матрицы А_i используются как оптимизируемые переменные в целевой функции для с-средних, что позволяет каждому кластеру адаптировать норму расстояния к топологической структуре данных. Целевая функция для ГК алгоритма определяется выражением . Целевая функция для ГК алгоритма не может быть непосредственно минимизирована относительно А_i, т.к. она (функция) является линейной по отношению к А_i. Чтобы найти допустимое (подходящее) решение, надо каким-нибудь путем ограничить А_i. Обычный путь достигнуть этого ограничить величину определителя А_i: . Позволение матрице А_i изменять свою величину при фиксированном значении ее определителя соответствует оптимизации формы кластера при сохранении его объема постоянным. Путем использования метода множителей Лагранжа Густафсоном и Кесселем было найдено следующее выражение для А_i: , где F_i представляет собой нечеткую ковариационную матрицу i-го кластера, определяемую как

.Заметим, что подстановка двух последних выражений в (21) дает обобщенный квадрат нормы Махаланобиса для расстояния. Алгоритм ГК является более сложным, чем алгоритм нечетких с-средних, т.к. в каждой итерации должны быть вычислены инверсия и определитель ковариационной матрицы.

Алгоритм Густафсона-Кесселя может быть сформулирован в следующем виде.

Дано множество данных X, выбрать число кластеров 1<c<K, параметр нечеткости m>1 , критерий остановки алгоритма и объемы кластеров _i. Инициализировать случайным образом матрицу разделения M ⁽⁰⁾.

Повторять для l=1,2,…

1.Рассчитать размещение центров (кластерных прототипов) в соответствии с формулой

,

2. Вычислить ковариационную матрицу для кластеров

,

3.Вычислить расстояния

4.Обновить матрицу разделения (матрицу степеней принадлежности всех векторов , j = 1, 2, ...,K, к центрам ν_i, i= 1, 2, ..., с,): Для , Если >0 для всех i=1,2,…,c

, иначе =0, если >0, и , .

До ||M ^(l)- M ^(l-1)||< .

Если последние изменения положений центров и матрицы ковариации пренебрежимо малы по отношению к предыдущим значениям и не превышают изначально заданной пороговой величины ε, то завершить итерационный процесс; в противном случае перейти к п. 2.

Функционирующий таким образом алгоритм обучения параллельно генерирует все центры самоорганизующихся кластеров и связанные с ними нормо-индуцирующие матрицы, используемые при расчете расстояний. Значения элементов нормо-индуцирующих матриц и положения центров фиксируются по завершению процесса обучения и могут использоваться в режиме эксплуатации системы.