2. Нечеткое инверсное управление и нечеткая система управления с внутренней моделью

1. Н ечеткое инверсное управление. Самый простой метод спроектировать нечеткий контроллер, используя принцип разомкнутого управления (без обратной связи), в котором нечеткий контроллер является инверсией объекта управления (обратным объектом управления) (см. рисунок ниже). В случае нелинейной модели объекта в результате получаем нелинейный нечеткий контроллер и, следовательно, в идеале приходим к абсолютно инвариантной системе. Пусть ОУ описывается нелинейным уравнением

y[i+1]=f(x[i],u[i]),где

x[i]=(y[i-1],…,y[i-n+1], u[i],…,u[i-m+1])^’.Выбирая контроллер u[i]=f ^-1(x[i],v[i+1]),получаем

y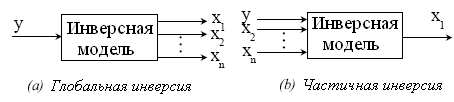 [i+1]=v[i+1]. Однако мы должны иметь в виду, что объект может обладать большим временем чистого запаздывания и это обстоятельство следует учитывать, и что для получения инверсной модели надо очень хорошо знать другие динамические и статические свойства объекта. Кроме того, надо понимать, что окончательная модель объекта никогда не будет точной копией реального объекта, и всегда имеют место воздействующие на объект возмущения, которые не были приняты в расчет при моделировании. Если нелинейная нечеткая модель найдена для частично неопределенного и весьма сложного по своим свойствам объекта, мы сталкиваемся с трудной проблемой получения инверсной модели. Кроме того, мы должны иметь в виду, что алгоритм для вычисления инверсной модели должен быть весьма быстрым, чтобы можно ее было использовать в реальном времени. Часто в качестве модели ОУ используют синглтонную нечеткую модель (см. далее). Этот тип модели принадлежит к общему классу аппроксиматоров функций. Другим типом модели, которая может быть точно инвертирована, является модель типа Такаги-Сугено.Мы должны помнить, что метод, основанный на инверсии, можно только применять к устойчивым ОУ с минимально-фазовыми свойствами. Мы обычно подразумеваем частичную, а не глобальную инверсию.Это означает, что в случае использования нечеткой модели для объекта с одним входом и одним выходом, для которой (нечеткой модели) дополнительными входами являются переменные состояния x₁,x₂,…,x_n, только одна из переменных состояния x₁ становится выходом инверсной модели, и выход модели y становится входом инверсной модели (см. рисунок выше).

У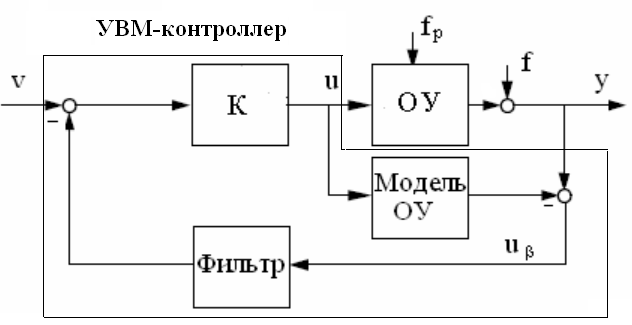 правление с нечеткой внутренней моделью. Чтобы преодолеть те проблемы, которые возникают при использовании метода, рассмотренного в предыдущем пункте и связанного с разомкнутой системой, было предложено дополнить структуру с инверсным управлением обратной связью. Это привело к появлению еще одного из возможных путей использования нечетких правил − применению управления с нечеткой внутренней моделью (УВМ). При этом функциональная схема системы управления (рис. 2.4) включает в себя, наряду с объектом управления (ОУ), три элемента: 1) нечеткую модель объекта управления, позволяющую предсказать реакцию ОУ на приложенное к нему управляющее воздействие u(t); 2) нечеткий инверсный контроллер, построенный как обратная нечеткая модель объекта управления; 3) фильтр, расположенный в цепи обратной связи. Если нечеткая модель точно описывает свойства объекта управления, и отсутствуют (идеальный случай) измеряемое возмущающее воздействие f(t), приведенное к выходу объекта, и не измеряемое возмущающее воздействие f_P(t), сигнал обратной связи (t) равен нулю и система работает как разомкнутая система. В случае, когда модель объекта идеальна, но имеет место измеряемое возмущение, сигнал обратной связи равен (t)= f(t) и не влияет непосредственно на управляющее воздействие, а просто вычитается из задающего воздействия v(t). В результате полностью исключается влияние f(t) на управляемую величину y(t). Фильтр вводится в обратную связь с целью повысить робастность системы к неопределенности модели объекта, учитываемой как действие не измеряемого возмущения f_p(t), и к шуму измерения. Если ошибки моделирования большие, то система может стать неустойчивой. При этом за счет фильтра можно избежать неустойчивой работы за счет снижения значений АЧХ разомкнутой системы на высоких частотах. Однако если ОУ проявляет нелинейные свойства, то нет возможности спроектировать фильтр заранее с учетом ошибок моделирования и возмущающих воздействий. Это обстоятельство представляет собой основную трудность проектирования такой системы.