37. Табличное изменение коэффициента усиления (супервизорное управление)

Рассмотрим использование контроллера Такаги-Сугено для супервизорного управления, понятие о котором было дано в параграфе 2.1. Пусть объект управления с существенно нелинейными свойствами (коэффициент усиления объекта y²(t) зависит от управляемой величины y(t)) описывается уравнением 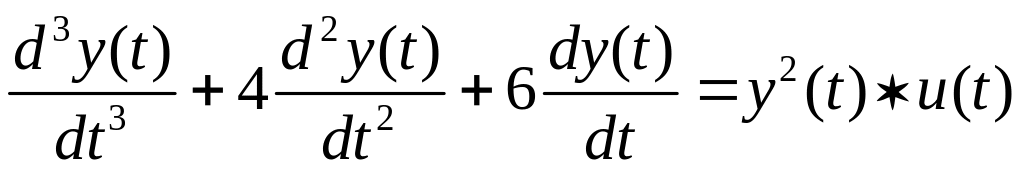.Структуру данного объекта можно представить как линейная часть с передаточной функцией ,

охваченная квадратичной обратной связью (рис.6). Цель управления заключается в том, чтобы обеспечить стабилизацию системы при изменении рабочей точки (состояния равновесия), т.е. значения y=const, в широких пределах при условии, что y 0. Проблемы, возникающие при использовании для этой цели четкого пропорционального регулятора с фиксированным коэффициентом усиления k_p, сводятся к следующему:

1.устойчивость и качество системы в сильной степени зависят от значения управляемой величины в состоянии равновесия;

2.настройка (подбор) коэффициента усиления k_p не позволяет добиться желаемой цели.

О тсюда приходим к выводу, что единственный путь решения поставленной задачи применить нелинейный закон управления, а именно, супервизорное управление, которое бы изменяло коэффициент усиления по нелинейному закону в зависимости от управляемой величины у. Предположим, что мы нашли желаемый закон изменения коэффициента усиления регулятора, обеспечивающий требуемое качество управления (рис.7).

Для реализации желаемого закона управления можно использовать различные способы аппроксимации, в частности, кусочно-линейную аппроксимацию или метод задания таблиц (look-up table) . Однако более удобно с точки зрения точности и быстроты вычислений применить нечеткий контроллер типа Такаги-Сугено. Заметим, что с помощью нечеткой логики можно, используя правила и функции принадлежности обеспечить аппроксимацию любой непрерывной функции с любой требуемой точностью, т.е. нечеткая модель Такаги-Сугено (ТСМ) при соответствующем выборе параметров является универсальным аппроксиматором непрерывной вещественной функции, которая определена в замкнутом и ограниченном множестве R_n . Это означает, что для любого >0 и для любой непрерывной функции g(x) существует ТСМ такая, что g(x) - y(x) < , где y(x) является выходом ТСМ. Рис. 7 иллюстрирует, каким образом можно аппроксимировать желаемую кривую изменения коэффициента усиления регулятора, используя три точки (другими словами, три правила) и тем самым осуществить супервизорное управление. Разумеется, чтобы повысить точность аппроксимации (подобно тому, как это делается в ряде Фурье), нужно еще добавить точки, и следовательно, правила, которые очевидно улучшат качество управления. Нечеткий контроллер, используемый для аппроксимации, значительно проще реализовать и настроить с помощью средств вычислительной техники, чем таблицы задания и кусочно-линейный аппроксиматор. В данном случае базовые правила выглядят так:

Если управляемая величина y большая, То коэффициент kp1,

Е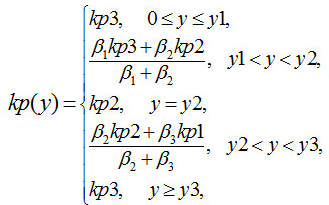 сли управляемая величина y средняя, То коэффициент kp2,

Если управляемая величина y малая, То коэффициент kp3.

При этом (смотри формулу).

Правила не аналогичны методу заданию таблиц, т.к. нечеткая арифметика интерполирует форму нелинейной функции. Показано, что объем памяти, требуемый для сохранения информации о функциях принадлежности и правил, значительно меньше, чем для таблиц задания, в особенности для систем с несколькими входами. В результате скорость вычислений может быть также повышена.