31. Проектирование нечетких контроллеров (метод Мамдани)

Нечеткие контроллеры с одним входом и одним выходом.

1. Нечеткий контроллер с одним входом и одним выходом

Пусть нечеткое правило, установленное с помощью экспертов, гласит: Если ошибка e есть , то управление u есть (2.15). Это правило называется лингвистической моделью нечеткого контроллера.

В результате измерений получено, что ошибка принимает другое лингвистическое значение, нечеткое множество . Делаем логический вывод: управление есть , в такой же степени близкое множеству , в какой степени близко к . Пусть ФП термов и определены и имеют вид и (рис. 2.7,а). Известна ФП для множества . Заметим, что множества и заданы на одном универсуме. При этом степень истинности утверждения «нечеткое множество близко к множеству » определяется композицией (шаг 1 алгоритма нечеткого логического вывода)

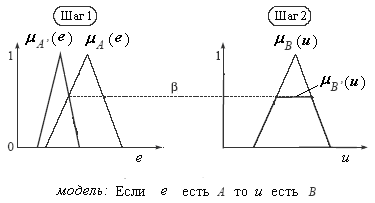(2.16)

Отсюда нечеткий логический вывод (заключение) приводит к ФП (шаг 2 алгоритма нечеткого логического вывода)

, (2.17) соответствующей множеству .Операция (2.17) называется активизацией правила. Весь алгоритм максиминной инференции графически иллюстрируется рис. 2.7,а. В системах управления представляет собой, как правило, четкое множество, включающее лишь один элемент (e-четкая (количественная) переменная), и его можно рассматривать как нечеткое множество с ФП , (2.18)

т.е. как синглтон (четкое число). Такой метод определения степени принадлежности называется синглтонной фаззификацией. При этом степень истинности

, (2.19) т.е. равна степени принадлежности при , другими словами, степени принадлежности, полученной при фаззификации (см. рисунок ниже).Для случая, когда есть синглтон с ФП (2.18), то в соответствии с (2.17)

(2.20)

В дальнейшем нас будет интересовать в основном только этот случай. Если нечеткое множество − синглтон с ФП (2.21)

то нечеткое множество будет представлять собой также синглтон с ФП

.

32. Нечеткая логика. Логические связки.

Логика начиналась с изучения естественного языка с точки зрения аргументов и убеждений и могла быть использована для суждения о корректности цепи высказываний, например в математических доказательствах. Заметим, что высказывание - мысль, выраженная повествовательным предложением и являющаяся истинной или ложной, а истина - адекватное отображение предметов и явлений познающим субъектом. В двухзначной (точной) логике высказывание является верным (истинным) или неверным (ложным), но не тем и другим. «Истина» или «ложь», приписываемые высказыванию, называются истинностными значениями (значениями истинности). В нечеткой логике нечеткое высказывание может быть верным или неверным или иметь промежуточные истинностные значения, например, может быть верно. Высказывание уровень высокий является примером такого высказывания в нечетком контроллере. По-видимому, удобно ограничить возможные истинностные значения в дискретной области, скажем значениями {0 0,5 1} для ложно, может быть верно, верно. В таком случае мы будем иметь дело с многозначной логикой, в данном случае, с трехзначной логикой. На практике разделение единичного интервала на меньшие части может быть более подходящим. При этом интервал {0 1} включает множество значений истинности нечетких высказываний.

Изначально Задэ интерпретировал значение истинности в нечеткой логике, например, Очень точно, как нечеткое множество. Таким образом, Задэ заложил в основание нечеткой (лингвистической) логики трактовку Истины как лингвистической переменной, значениями которой являются скорее слова или высказывания, чем числа.

Логические связки (соединения)

В ежедневных разговорах и в логике фразы (высказывания) связывают с помощью слов не, и, или, если - то (или импликация) и если и только если. Эти слова называют связками. Высказывание, которое модифицируется с помощью слова «не», называется отрицанием исходного высказывания. Слово «и» используется, чтобы объединить два высказывания в форме конъюнкции (от conjunction - союз, связь) двух высказываний. Аналогично высказывание, которое образовано путем соединения двух высказываний с помощью слова «или», называется дизъюнкцией (от disjunction − разобщение) двух высказываний. Из двух высказываний мы можем построить некое высказывание с помощью формы «Если…то…»; последнее называют условным высказыванием (предложением). Высказывание, стоящее за словом «Если», называется антецедентом (предпосылкой), а высказывание, следующее за словом «то», называют консеквентом (следствием) или заключением. Таким образом, антецедент является первой частью условного высказывания (предложения), а консеквент – второй частью этого условного высказывания. Другие идиомы (словосочетания), которые мы будем считать, имеющими то же самое значение (тот же самый смысл), что «если p, то q» (где p и q есть высказывания), звучат как «p влечет за собой q», «p только, если q»,

«q, если p» и т.п. Слова «если и только если» (или эквивалентность) используются, чтобы из двух высказываний образовать двухусловное высказывание, которое принимает значение истина в случае истинности обоих высказываний одновременно и значение ложь в остальных случаях. Надо сказать, что операция, называемая импликацией высказываний (от implico – тесно связываю), в общем случае отличается от базового правила (правила продукции) Если A, то B. Действительно, логическая импликация высказываний не заключает в себе никакой причины, никакой временной или иной взаимосвязи между предпосылкой и следствием.

Путем введения букв и специальных символов структура связок может быть показана красноречивым образом. Наш выбор символов имеет такой вид

для «не» (отрицание)

для «и» (конъюнкция)

для «или» (дизъюнкция)

для «если-то» (импликация)

для «если и только если» (эквивалентность)

В нечеткой логике расширения «не», «и» и «или» также называют нечетким отрицанием, T-нормой и S-нормой соответственно.