28. Обратное распространение ошибки

Метод обратного распространения ошибки представляет собой популярную процедуру обучения многослойного персептрона. Он основан на дельта-правиле и использует критерий качества обучения (сумму квадратов ошибок e_j=d_j-y_j) 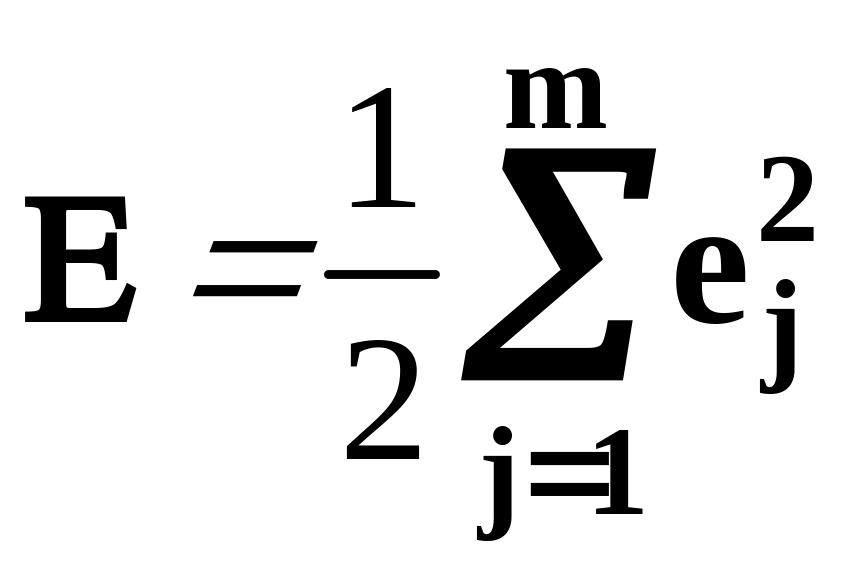(5) для нейронов выходного слоя. Этот критерий есть сумма квадратов ошибок, получаемых на выходе каждого нейрона выходного слоя. Весовой коэффициент передачи сигнала от p-го нейрона предыдущего слоя к q-му нейрону последующего слоя обновляется в соответствии с обобщенным дельта-правилом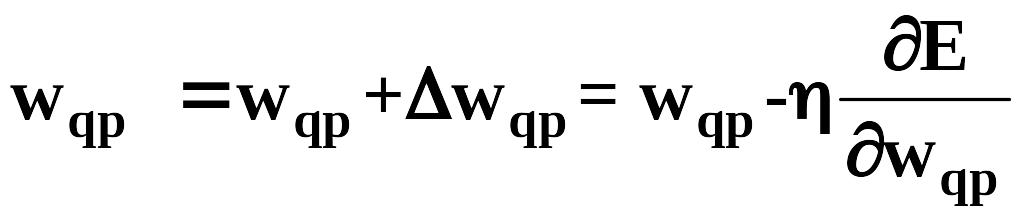 (6). Чтобы обозначения были более понятными, мы опустили индекс обучающего образца k; очевидно, что уравнение (6) является рекуррентным, т.е. в его левой части представляет новое значение весового коэффициента, в то время как в правой части является прежним весом. Здесь - параметр скорости обучения. В обобщенном дельта-правиле корректировка весового коэффициента пропорциональна градиенту ошибки / , другими словами, чувствительности критерия качества к изменению весового коэффициента. Чтобы применить данный алгоритм, необходимы два цикла вычислений, прямое распространение и обратное распространение. В прямом цикле вычислений веса остаются неизменными. Прямое распространение сигнала начинается в последнем скрытом слое, ведя счет от выходного слоя, путем подачи на его вход образцового входного векторного сигнала и заканчивается в выходном слое после вычисления сигнала ошибки (разности между образцовым выходным сигналом и выходным сигналом нейрона) для каждого нейрона выходного слоя. Обратное распространение сигнала начинается в выходном слое и продолжается путем распространения сигнала ошибки назад справа налево через всю сеть, слой за слоем. Для описания алгоритма обратного распространения сигнала ошибки предположим, что j – й нейрон является нейроном выходного слоя (рис. 7). На рис. 7 показаны в явном виде связи между нейроном j выходного слоя, нейроном i скрытого слоя 1, нейроном r скрытого слоя 2 и нейроном s скрытого слоя 3.

З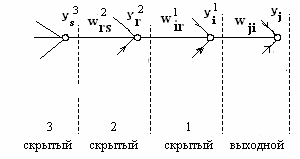 аменяя в (6) q на j и p на i, получаем формулу для настройки весовых коэффициентов выходного слоя 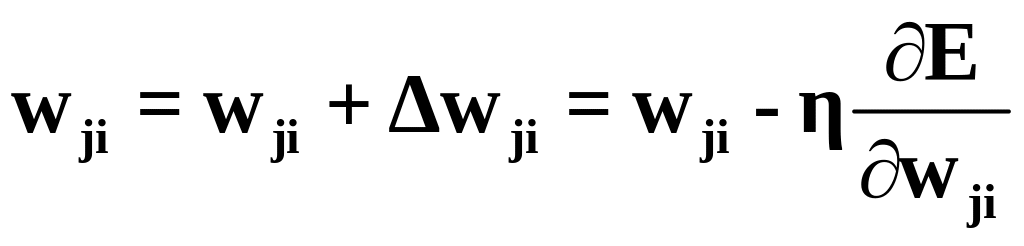(6а). Используя цепное правило дифференцирования, запишем производную, входящую в уравнение (6а), в виде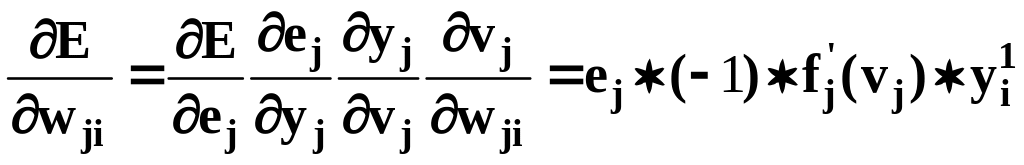 (7). Здесь с учетом (5)

= = - есть ошибка j-го нейрона, есть выход j-го нейрона, 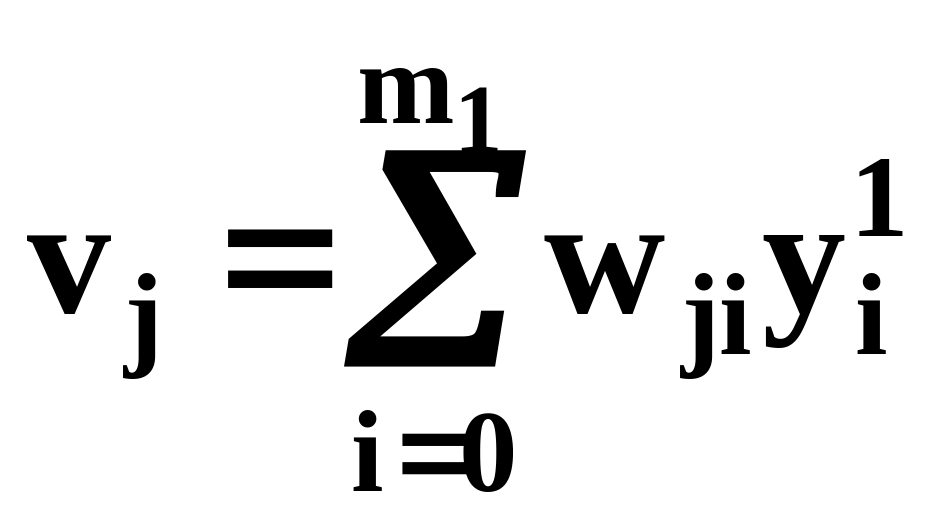есть внутренний вход j-го нейрона, полученный на основании (4c) 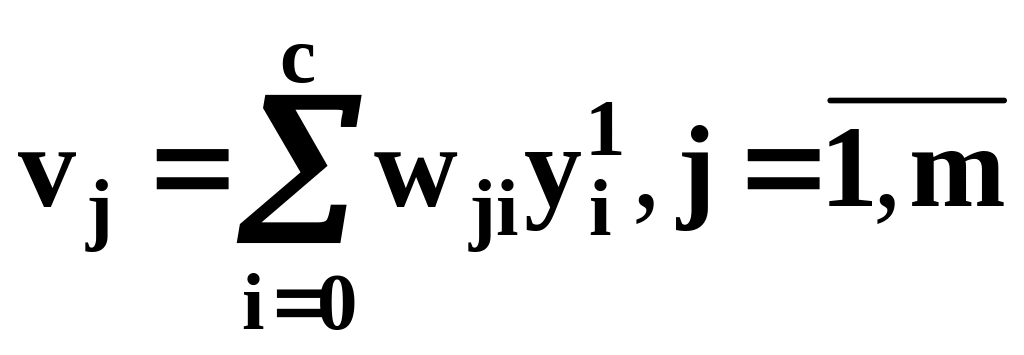, после суммирования взвешенных выходов всех нейронов m₁ предшествующего первого скрытого слоя, в том числе выхода i-го нейрона этого слоя, есть весовой коэффициент передачи сигнала от i-го нейрона первого скрытого слоя к входу j-го нейрона выходного слоя. При этом ,где - активационная функция. Как обозначена производная от функции по ее аргументу. С учетом (7) и (4c) при c= m₁, находим с помощью (6а) 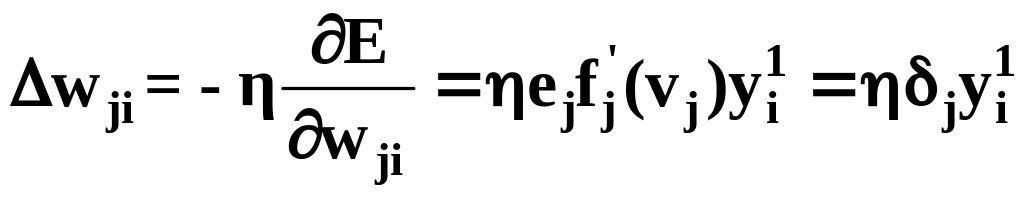, (8) где (8a). Как видим, для обновления весовых коэффициентов выходного слоя надо найти ошибку , выход i-го первого скрытого слоя и производную .

Алгоритм. Алгоритм обратного распространения включает пять шагов.

а) Инициализация весовых коэффициентов. Установите все весовые коэффициенты равными небольшим случайным числам.

б) Предъявление входов и соответствующих им желаемых выходов (обучающие пары). Подаем на нейронную сеть вектор входа u и соответствующий желаемый вектор выхода d. Вход может быть новым в каждой новой попытке обучения или образцы из обучающего множества могут подаваться на сеть циклически до тех пор, пока весовые коэффициенты не стабилизируются, т.е. перестанут изменяться.

в) Вычисление действительных значений выхода. Вычисляем вектор выхода последовательно используя выражение , где f есть вектор активационных функций.

г) Настройка весовых коэффициентов. Начинаем настройку с весов выходного слоя и затем идем назад к последнему скрытому слою (считая справа налево). Весовые коэффициенты настраиваем с помощью

(21). В этом уравнении есть весовой коэффициент соединения, связывающего нейрон p скрытого слоя с нейроном q следующего слоя, - выход нейрона p (или внешний вход для нейрона q), есть параметр скорости обучения и - градиент. Если нейрон q является нейроном выходного слоя, то вычисляется с помощью (19) и если нейрон q является нейроном скрытого слоя, то определяется с помощью (20) 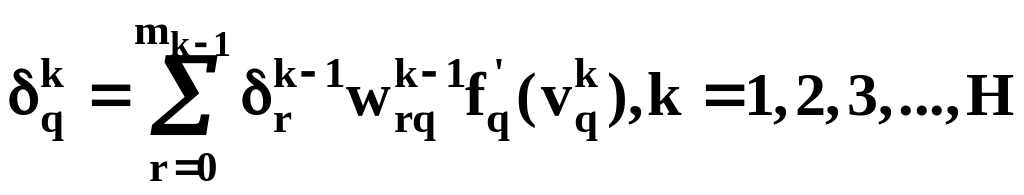. Ускорение сходимости можно иногда обеспечить, если добавить значение момента. Замечание. Для пакетного режима обработки дельта-правило (6) модифицируется

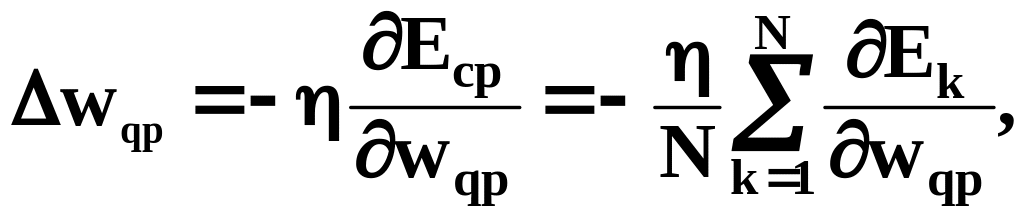
где вычисляется в режиме онлайн и затем накапливается в процессе представления обучающих данных для , как составная часть обратных вычислений. Как видим, весовые коэффициенты обновляются после представления всех обучающих данных. Алгоритм онлайн проще для реализации и требует меньше памяти, чем алгоритм офлайн. Однако алгоритм онлайн обеспечивает более точную оценку вектора градиента и более простую сходимость к локальному минимуму.