
- •1.Коньюнкция условий и разбиение пространства входа.
- •Композиция нечетких отношений.
- •Нечеткое инверсное управление и нечеткая система управления с внутренней моделью
- •Алгоритм жесткой кластеризации.
- •Операции над нечеткими множествами. Модификаторы.
- •8. Проектирование нечетких контроллеров (метод Мамдани)
- •2. Нечеткий контроллер с двумя входами и одним выходом
- •9.Нечеткая система управления с плановым изменением коэффициента.
- •10. Оценка параметров заключений по (мнк)
- •11. Адаптивные нейронные нечеткие системы инференции (anfis)
- •12.Импликация Мамдани. Внешнее произведение.Таблица импликаци
- •13. Нечеткая идентификация. Структура и параметры.
- •14. Нечеткий логический вывод для нескольких правил и нескольких входов.
- •Несколько входов (многомерная лингвистическая модель)
- •16. Функциональная схема нечеткого контроллера
- •17. Отношения между нечеткими множествами
- •18. Алгоритм нечеткой кластеризации с-средних
- •19. Моделирование статических объектов упр-я как аппроксимация функций с помощью нейронных сетей (есть только для динамических объектов)((((((((
- •20. Анализ устойчивости тс модели объекта управления в пространстве состояний.
- •22. Нечеткий логический вывод с исп-м отношений. Пример
- •24. Визуализация алгоритма нечеткого логического вывода.
- •25. Понятия о нечетких множествах
- •26. Обучение нейронной сети. Общие сведения.
- •27. Упрощение алгоритма нечеткого логического вывода.
- •28. Обратное распространение ошибки
- •29. Визуализация нечеткого логического вывода.Аккумуляция.
- •30. Параметры алгоритма с-средних
- •31. Проектирование нечетких контроллеров (метод Мамдани)
- •32. Нечеткая логика. Логические связки.
- •33.Проектирование нечетких контроллеров(метод Мамдани). Многомерный нечеткий контроллер.
- •34. Алгоритм обучения anfis
- •35. Максиминная композиция нечетких отношений. Внутренне произведение. Пример.
- •36. Преобразование вход-выход. Кривая управления. Пов-ть управления.
- •37. Табличное изменение коэффициента усиления (супервизорное управление)
- •38. Алгоритм нечеткой кластеризации Густафсона–Кесселя.
- •39. Генетические алгоритмы
- •40. Извлечение правил с помощью кластеризации
- •41.Нечеткий сумматор для контроллеров с 2 входами и 1 выходом
- •42. Нейросетевое прямое и косвенное адаптивное управление с эталонной моделью
- •43. Обратное распространение ошибки. Обновление весовых коэф-в скрытых слоев. Локальные градиенты.
- •44. Модель Такаги-Сугено как квазилинейное устройство
- •45. Контроллер типа Такаги-Сугено
- •46. Нейросетевое управление с адаптивной линеаризацией обратной связью
- •48. Такаги-Сугено модель оу в пространстве состояний
- •49. Нечеткие множества. Синглтоны и лингвистические переменные.
- •50. Моделирование нелинейных динамических оу с помощью нейронных сетей
- •51. Структура интеллектуальной системы управления
- •52. Многослойная нейронная сеть
- •53. Дефаззификация. Методы дефаззификации.
- •54. Нейронная сеть с радиальными базисными функциями
- •56. Синтез нечеткой обратной связи
- •57. Линейные матричные неравенства, основные понятия.
- •58. Аппроксимация функций (моделирование) с помощью нейронных сетей (персептронов)
- •59. Классификация генетических нечетких систем
- •60. Синтез нейронных нечетких сетей. Структура anfis
- •19. Моделирование статических объектов управления как аппроксимация функций с помощью нейронных сетей.
- •Адаптивные нейронные нечеткие системы интерференции (anfis). . Синтез нечетких нейронных сетей
- •5.1. Введение
- •Адаптивные нейронечеткие системы инференции (anfis)
- •Импликация Мамдани. Внешнее произведение. Таблица импликации.
- •Нечеткая идентификация. Структура и параметры
- •Нечеткий логический вывод для нескольких правил и нескольких входов.
- •1. Настройка пид-регулятора
- •3. Перенос параметров пид-регулятора в нечеткий контроллер
- •Анализ устойчивости тс модели объекта управления в пространстве состояний. Анализ устойчивости тс модели объекта
- •1. Настройка пид-регулятора
- •Нечеткий логический вывод (инференция). Пример.
- •Визуализация нечеткого логического вывода. Агрегирование условий и активизация заключений.
- •Математическая модель нейрона. Математическая модель нейрона
- •Нечеткое управление с предсказанием.
- •Визуализация нечеткого логического вывода. Аккумуляция заключений.
- •5.1. Введение
- •Алгоритм обучения anfis
- •Максиминная композиция нечетких отношений. Внутреннее произведение. Пример.
- •Преобразование вход-выход для нечетких контроллеров. Кривая управления и поверхность управления.
- •2.4. Преобразование вход-выход
- •Табличное изменениекоэффициентаусиления (супервизорное управление).
- •2.8. Табличное изменение коэффициента усиления (супервизорное управление)
- •Алгоритм нечеткой кластеризации Густафсона-Кесселя.
- •Генетические алгоритмы. Генетические алгоритмы
- •Модель Такаги-Сугено как квазилинейное (аффинное) устройство. Модель Такаги-Сугено как квазилинейное устройство
- •Контроллер типа Такаги-Сугено.
- •Деффазификация. Методы деффазификации.
- •2.2.5. Дефаззификация
- •Теорема б универсальной аппроксимации.
- •Такаги-Сугено модель объекта управления в пространстве состояний.
- •Табличный контроллер. Билинейная интерполяция.
- •2.3. Табличный контроллер
- •Моделирование нелинейных динамических объектов управления с помощью нейронных сетей.
- •Моделирование нелинейных динамических процессов (объектов)
- •Упрощение алгоритма нечеткого логического вывода.
- •Обратное распространение ошибки. Обновление весовых коэффициентов выходного слоя.
- •4.6. Обратное распространение ошибки
- •Структура интеллектуальной системы управления.
- •Многослойная нейронная сеть. Многослойная нейронная сеть
- •5.1. Введение
- •Структура anfis
25. Понятия о нечетких множествах
Нечеткие множества представляют собой развитие математического понятия множества. Впервые множества начал исследовать немецкий математик Георг Кантор (1845-1918). Созданная им теория множеств встречала возражения в течение всей его жизни. Однако в настоящее время большинство математиков поверило в возможность представления многих, если не всех разделов математики на языке теории множеств. Многие ученые обратили внимание на важность «фаззификации» (нечеткости) в теории множеств и большое количество литературы, посвященное этой проблематике, является доказательством такого внимания. Для специалистов в области управления нечеткая логика и нечеткие отношения являются самыми важными понятиями для того, чтобы разобраться в механизме действия нечетких правил. Традиционные (общепринятые, четкие) множества. Множество есть любая совокупность элементов (предметов) произвольной природы, которые можно трактовать как единое целое. Кантор описывал множество посредством его членов так, что отдельные предметы из данного универсума (окружающего мира) являются его (множества) членами или нет. Понятия множества, совокупности, класса, так же как понятия предмет, элемент, член являются синонимами. Вообще любое нечто, названное в обыденном разговоре множеством является множеством и в математическом смысле.
Пример 1.1 (множества). Следующие списки или совокупности предметов хорошо определены, что дает право назвать их множествами:а) множество неотрицательных чисел меньших чем 4. Это конечное множество с четырьмя элементами 0, 1, 2 и 3; б) множество живых динозавров в подвалах Палеонтологического музея в г. Москве. Это множество не содержит ни одного элемента и поэтому называется пустым множеством; в) множество числовых результатов измерения напряжения, превышающих 10 вольт. Хотя это множество является бесконечным множеством, однако нетрудно ответить на вопрос является ли результат данного измерения напряжения его элементом или нет.
Множество можно определить, перечисляя его элементы. Эти элементы полностью характеризуют множество. Список элементов A={0,1,2,3} полностью определяет конечное множество (конечное число элементов). Нельзя перечислить все элементы бесконечного множества. Поэтому мы должны вместо списка указать некоторое свойство, присущее всем элементам множества, например, используя предикат (утверждение) x>10. Такое множество определяется элементами из окружающего мира (универсума), для которых утверждение является истинным. Таким образом, имеются два пути описания множества: явно с помощью списка либо неявно с помощью предиката.
Классическое (четкое) множество имеет четкие границы. Так классическое множество A, фигурирующее в примере в) может быть выражено как , что ясно, недвусмысленно говорит о граничном значении, равном 10. При этом , если x меньше, чем это число, то x принадлежит множеству A, в противном случае x не принадлежит этому множеству.
Н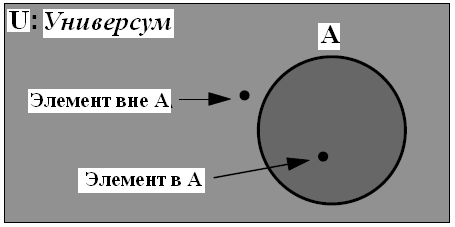
 ечеткие
множества. Следуя идеям Заде, заметим,
что многие множества для определения
своих элементов требуют другие критерии
(границы), чем один критерий вида или-или
(например, напряжение или меньше или
больше 10 вольт). Заде предложил использовать
понятие степень принадлежности, чтобы
переход от «принадлежности элемента к
множеству» к «непринадлежности элемента
множеству» был нерезким, а постепенным,
плавным, т.е. границы нечеткого множества,
что следует из его названия являются
нечеткими, размытыми. При этом степень
принадлежности, заданная для всех его
элементов, называется функцией
принадлежности и описывает полностью
нечеткое множество. Степень принадлежности
конкретного элемента множества
представляет собой обычно положительное
вещественное число, расположенное в
диапазоне от 0 до 1 и часто обозначаемое
греческой буквой
.
Чем больше такое число, тем больше
степень принадлежности.Заде рассматривал
множество Кантора как особый случай,
при котором все элементы x
множества A имеют полную
степень принадлежности
=1,
а те, которые не принадлежат множеству,
имеют степень принадлежности, равную
нулю, т.е.
.
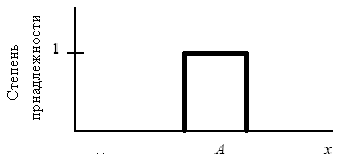
При этом функция принадлежности
такого множества A
определяется как
Он
назвал, между прочим, множество Кантора
ненечетким; в настоящее время для такого
названия используется термин четкое
множество, что позволяет избежать
некоторых дилемм (затруднительных
положений). Заметим, что Заде не дал
формальной основы для определения
степени принадлежности. Степень
принадлежности является определенным
числом, однако, субъективной мерой,
зависящей от ситуации (окружающей
обстановки) и обстоятельств.
ечеткие
множества. Следуя идеям Заде, заметим,
что многие множества для определения
своих элементов требуют другие критерии
(границы), чем один критерий вида или-или
(например, напряжение или меньше или
больше 10 вольт). Заде предложил использовать
понятие степень принадлежности, чтобы
переход от «принадлежности элемента к
множеству» к «непринадлежности элемента
множеству» был нерезким, а постепенным,
плавным, т.е. границы нечеткого множества,
что следует из его названия являются
нечеткими, размытыми. При этом степень
принадлежности, заданная для всех его
элементов, называется функцией
принадлежности и описывает полностью
нечеткое множество. Степень принадлежности
конкретного элемента множества
представляет собой обычно положительное
вещественное число, расположенное в
диапазоне от 0 до 1 и часто обозначаемое
греческой буквой
.
Чем больше такое число, тем больше
степень принадлежности.Заде рассматривал
множество Кантора как особый случай,
при котором все элементы x
множества A имеют полную
степень принадлежности
=1,
а те, которые не принадлежат множеству,
имеют степень принадлежности, равную
нулю, т.е.
.
При этом функция принадлежности
такого множества A
определяется как
Он
назвал, между прочим, множество Кантора
ненечетким; в настоящее время для такого
названия используется термин четкое
множество, что позволяет избежать
некоторых дилемм (затруднительных
положений). Заметим, что Заде не дал
формальной основы для определения
степени принадлежности. Степень
принадлежности является определенным
числом, однако, субъективной мерой,
зависящей от ситуации (окружающей
обстановки) и обстоятельств.
