24. Визуализация алгоритма нечеткого логического вывода.

Р ассмотрим изложенную технологию инференции применительно к рис. 2.8 и 2.10. Эти рисунки визуально отображают алгоритм, положенный в основу работы нечеткого ПД – контроллера. Например, первый ряд на рис. 2.8 говорит о том, что, если ошибка отрицательная (ряд 1, столбец 1) и скорость изменения ошибки отрицательная (ряд 1, столбец 2), то выход должен быть отрицательным и большим (по абсолютному значению).

Представленная на рис. 2.8 диаграмма целиком и полностью соответствует базовым правилам (2.2).

1.Если ошибка - и скорость изменения ошибки -, то выход ОтрБ.

2.Если ошибка - и скорость изменения ошибки 0, то выход ОтрС.

3.Если ошибка - и скорость изменения ошибки +, то выход Нуль.

4.Если ошибка 0 и скорость изменения ошибки -, то выход ОтрС.(2.2)

5.Если ошибка 0 и скорость изменения ошибки 0, то выход Нуль. 6.Если ошибка Нуль и скорость изменения ошибки Пол, то выход ПолС. 7.Если ошибка Пол и скорость изменения ошибки Отр, то выход ОтрБ. 8.Если ошибка Пол и скорость изменения ошибки Нуль, то выход ПолС. 9.Если ошибка Пол и скорость изменения ошибки Пол, то выход ПолБ.

В данном случае r=2 (ошибка и скорость изменения ошибки), число термов по каждому входу n₁ =n₂ =3, так что в соответствии с (2.32,д) требуемое число правил N=3*3=9. Число термов выхода q = 5<9.

Эти правила воплощают стратегию (закон) управления, согласно которому управляющий сигнал должен быть комбинацией упоминаемой ошибки и скорости изменения ошибки в нечетком пропорционально-дифференциальном контроллере. Мгновенные значения ошибки и скорости ее изменения определяют положение вертикальных линий в первом и втором столбцах диаграммы. В рассматриваемом случае ошибка e= e’=0 и скорость ее изменения ce= =ce’ =-55.5. Для каждого правила алгоритм инференции отыскивает значения функций принадлежности в части условий (предпосылок, антецедент) правил, т.е. отыскивает степени принадлежности для каждого правила (синглтонная фаззификация).

Агрегирование (конъюнкция) условий. Агрегирование – операция, используемая для вычисления степени выполнения (истинности) или возбуждающей силы условий i – го правила. Каждое правило, например правило 1, порождает степень принадлежности , соответствующую измеренному значению ошибки, и степень принадлежности , соответствующую измеренному значению скорости изменения ошибки. Тогда агрегирование согласно (2.25) и (2.28) является их конъюнкцией . Подобная операция осуществляется в отношении всех других правил. Агрегирование условий эквивалентно фаззификации, если контроллер имеет лишь один входной сигнал. Агрегирование условий иногда называют выполнением или вычислением возбуждающей силы левой части правил.

Активизация. Активизация (активация) - нечеткий логический вывод (заключение) для каждого правила, возможно, связанный с ослаблением их возбуждающей силы заключения. Длина черных вертикальных линий в третьем столбце на рис. 2.8 согласно формуле активизации (2.17) определяет возбуждающую силу заключения каждого i-го правила. Причем активизирована лишь часть синглтонов, а именно синглтоны, соответствующие первому, второму, четвертому, пятому, седьмому и восьмому правилам. В качестве операторов конъюнкции (активизации) используются операторы min или алгебраического произведения *, которым соответствует, как говорят, min-активизация и prod-активизация. В данном случае (рис. 2.8) вид используемого оператора не играет никакой роли, т.к. функциями принадлежности выхода (управляющего сигнала) являются синглтоны.

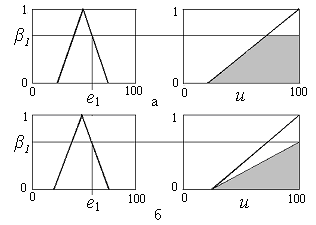
Однако в общем случае в третьем столбце фигурируют функции принадлежности другого вида, например, образные функции принадлежности. При этом prod-активизация (рис. 2.9,б) масштабирует график функции принадлежности выхода, таким образом, сохраняя его (графика) первоначальную форму и не ограничивая (не обрезая, не усекая) ее, как это имеет место при использовании min-активизации (рис. 2.9,а). Оба метода, в общем, работают хорошо, однако в результате использования операции алгебраического произведения (умножения) получаем несколько более сглаженный управляющий сигнал. Правило с номером i может быть априорно взвешено с помощью весового коэффициента , который называют степенью уверенности (доверия). При этом возбуждающая сила (степень истинности) такого правила изменяется и принимает вид, . Степень доверия определяется проектировщиком системы или обучающая программа пытается путем изменения этой степени адаптировать правила так, чтобы они в наибольшей мере соответствовали некоторой приемлемой зависимости вход-выход.