17. Отношения между нечеткими множествами

В любом нечетком контроллере отношения между множествами играют главную роль. Понятие нечеткого отношения, наряду с понятием самого нечеткого множества, следует отнести к фундаментальным основам всей теории нечетких множеств. Нечеткое отношение часто заменяется терминами нечеткая связь, ассоциация, взаимосвязь или соотношение. Некоторые отношения затрагивают элементы одного и того же универсума или, как говорят, описывает свойство: например, такие свойства «одно измерение больше другого», «одно событие наступает раньше другого», «один элемент похож на другой элемент» и т.п. Другие отношения связывают элементы из разных универсумов, например, описывают такие свойства, как «величина измерения большая и его скорость изменения положительная», «x- координата (абсцисса) большая и y- координата (ордината) малая». В этих примерах фигурируют отношения между двумя множествами. Однако в принципе могут иметь место отношения, устанавливающие связи между несколькими множествами.

Формально бинарное четкое отношение или просто четкое отношение R между двумя четкими множествами и (отношение между элементами x и y множеств и ) в соответствии с заданным свойством приписывает каждой упорядоченной паре только лишь одно из следующих утверждений: а) «x связано с y» или б) «x не связано с y». Продукционное пространство или декартово произведение множеств есть множество всех возможных комбинаций (пар) элементов (значений) из и или это то же, что для всех , т.е.

.

Пример. Пусть есть множество женщин {Ольга, Вера, Галина} и есть множество мужчин {Борис, Николай, Сергей}, то отношение «состоят в браке» на множестве может быть, например, таким

{(Ольга, Сергей),(Вера, Николай),(Галина, Борис)}.При этом данное отношение можно описать двумерной функцией принадлежности

Заметим, что в классической теории множеств называют характкристической функцией. Нечеткое отношение R между множествами A и , называемое бинарным (двумерным) нечетким множеством, есть нечеткое подмножество декартового произведения соответствующих этим множествам универсумов A и B. При этом двумерная функция принадлежности , описывающая нечеткое отношение, показывает степень выполнения отношения между элементами x и y, ,

Отсюда нечеткие отношения являются более гибкими по сравнению с традиционными (четкими) отношениями. Они позволяют задавать не только сам факт выполнения соотношения, но и указывать степень его выполнения, что является очень важным для многих практических задач, в частности для задач управления. Нечеткое отношение R между множествами A и называют бинарным (двумерным) нечетким множеством с двумерной функцией принадлежности . Если множество A состоит из m элементов, а множество из элементов, то является матрицей размерности ( ). По сути дела нечеткое отношение можно считать тождественным своей функции принадлежности , т.е. можно записать, что .

П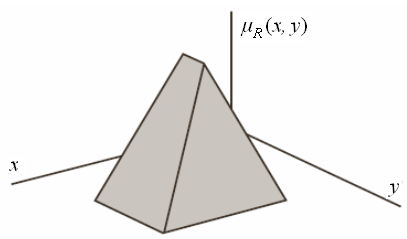 ример 2. Еще один пример функции принадлежности нечеткого отношения R в случае, когда имеет место треугольная функция принадлежности для A и трапециидальная функция принадлежности для B, показан на рисунке ниже. При этом нечеткое отношение описывает свойство (импликацию):

« если x есть A, то y есть B».