16. Функциональная схема нечеткого контроллера

Имеются характерные специфические компоненты (элементы) нечеткого контроллера, обеспечивающие процедуру проектирования. На блок-схеме нечеткий статический преобразователь (рис. 2.5), другое название система нечеткого логического вывода (Fuzzy Inference System (FIS)), расположен между блоком препроцессора и блоком постпроцессора. Ниже опишем назначение каждого из блоков, представленных на этом рисунке.

Препроцессор: Входные сигналы нечеткого контроллера являются результатом

ф изических или, другими словами, четких измерений величин, полученных от датчиков, а не лингвистические переменные, другими словами, содержат количественную информацию. Препроцессор, первый блок на рис. 2.5, подвергает обработке сигналы измерений перед тем, как они поступят на вход статического преобразователя (статического контроллера). Примерами предварительной обработки могут служить следующие операции: дискретизация и квантование по уровню (округление до целых чисел); нормализация или масштабирование входных сигналов с той целью, чтобы эти сигналы не выходили за пределы определенного стандартного диапазона; фильтрация с целью подавления шума; усреднение, чтобы выявить тенденции поведения входных сигналов в близком или далеком будущем; комбинация нескольких измерений, чтобы выделить ключевые измерительные сигналы; дифференцирование и интегрирование или их дискретные эквиваленты, например дискретный интегратор, вычислитель первой разности (дискретный дифференциатор). Квантование по уровню необходимо, чтобы преобразовать входной сигнал с целью определить самый лучший шаг квантования по уровню в дискретном универсуме. Пусть, например, переменная ошибка e принимает значение 4,5. Однако дискретный универсум является множеством u = [-5 -4 …0…4 5]. При этом квантователь должен округлить значение 4,5 до 5, ближайшего целого значения. Квантователь позволяет уменьшить число возможных различных значений, снимаемых с его выхода, по сравнению с входными данными. Однако слишком грубое квантование (квантование с большим шагом квантования по уровню) может повлечь за собой возникновение в системе незатухающих колебаний в окрестности желаемого состояния равновесия системы или даже неустойчивость системы.

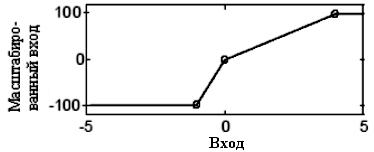
Нелинейное масштабирование является опцией (необязательной операцией). В нечетком контроллере Шмидта контроллер запрашивает у оператора 3 (три) числовых значения для малого, среднего и большого по величине измерения соответственно. Эти значения определяют точки излома кривой, с помощью которой масштабируются входные измерения (рис. 2.6). Общий эффект можно интерпретировать как искажение первоначального нечеткого множества. В дальнейшем такой эффект может стать причиной затруднений, связанных как с масштабированием, так и с усилением сигнала в контроллере, что, в свою очередь, затрудняет настройку последнего.

Если входным сигналом нечеткого контроллера является ошибка e, закон управления может быть представлен в виде статической характеристики, u=f(e),связывающей выходной u и входной e сигналы контроллера. Динамический контроллер должен иметь дополнительные входные сигналы, например, производные, интегралы от ошибки или прошлые измерения ошибки и выхода. Такие дополнительные сигналы вырабатываются в препроцессоре. При этом получаем многомерный контроллер (контроллер с несколькими входными сигналами). Проектирование подобного контроллера связано с применением большего числа базовых правил и является более сложным, чем проектирование контроллера с одним входным сигналом. Выходной сигнал препроцессора поступает на вход статического нечеткого контроллера.

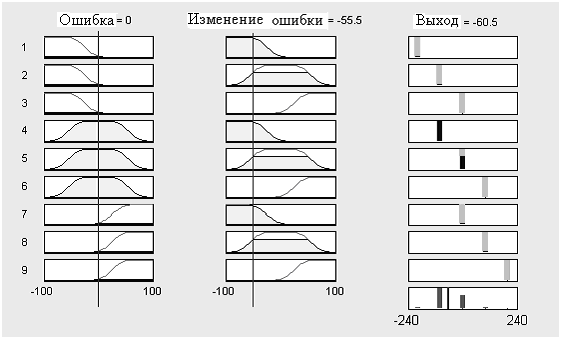
Фаззификация: Первый блок внутри статического преобразователя (контроллера) осуществляет фаззификацию, т.е. преобразует каждое значение входного сигнала (физическую переменную) в степень принадлежности посредством просмотра одной или нескольких функций принадлежности, другими словами, преобразует количественную информацию в качественную. Блок фаззификации таким образом устанавливает соответствие входного сигнала предпосылкам базовых правил с целью определить насколько хорошо предпосылки каждого правила соответствуют данному конкретному значению входного сигнала. В результате фаззификации определяются степени принадлежности для каждого лингвистического терма применительно к этому конкретному значению входа.

Базовые правила (лингвистическая модель нечеткого статического преобразователя)Правила, описывающие лингвистическую модель нечеткого статического преобразователя, могут использовать несколько лингвистических переменных (термов), как в предпосылках, так и в заключениях правил. Поэтому контроллеры могут быть применимы как для задач управления в системах с одним входом и одним выходом (одномерными системами), так и для задач управления в системах с несколькими входами и несколькими выходами (многомерными системами). Типичная задача управления объектом с одним входом и одним выходом – изменять управляющее воздействие (управляющий сигнал), используя сигнал ошибки. При этом принцип управления называется управлением по ошибке (по отклонению). Для успешной работы контроллера могут потребоваться в качестве его (контроллера) входных сигналов не только сигнал ошибки, но и скорость изменения ошибки (производная от ошибки), и интеграл от ошибки. Однако их можно вычислить, используя одноконтурную систему управления, т.к. все три упомянутых переменных формируются из полученной в результате измерения ошибки.

Формы представления (форматы) правил. По сути дела нечеткий (лингвистический) контроллер содержит правила (нечеткую базу знаний или лингвистическую модель) в виде если – то, однако эти правила могут быть представлены в различных форматах. Во многих случаях для конечного пользователя правила представляют в формате, подобном приведенному ниже.

1. Если ошибка Отр и скорость изменения ошибки Отр, то выход ОтрБ.

Н азвания Нуль, Пол, Отр являются аббревиатурой названия нечетких множеств, так же как и названия ОтрБ, ОтрС, ПолБ, ПолС (отрицательное большое, отрицательное среднее, положительное большое и положительное среднее соответственно). Второй формат – табличный лингвистический формат, более компактный. Входные переменные (сигналы) и их термы записывают вдоль сторон (верхней и левой боковой) таблицы, а термы выходной переменной – внутри таблицы.

Если в таблице осталась пустая ячейка, это говорит о том, что пропущено одно из правил. Следовательно, такой формат полезен для оценки комплектности (полноты) правил. Когда входными сигналами являются ошибка и скорость изменения ошибки, этот формат называют лингвистической фазовой плоскостью. Если число используемых входных сигналов больше двух, т.е.

n > 2, таблица перерастает в n-мерный массив, очевидно, неудобный для пользователя.Чтобы приспособить табличный формат на случай нескольких входных сигналов, вероятно, надо переделать ячейки таблицы. Надо отметить, что правило с несколькими выходными сигналами может быть разбито на совокупность нескольких правил, каждое с одним вспомогательным выходом. Наконец, также можно использовать графический формат, который отображает функции принадлежности. Этот графический интерфейс пользователя отражает процесс инференции лучше, чем другие форматы, однако занимает много места на экране монитора..

Выбор универсума. Элементы нечеткого множества берутся из универсального множества или универсума. Универсум содержит все элементы, которые могут быть приняты к рассмотрению. Прежде чем конструировать функции принадлежности, необходимо выбрать универсумы для входных и выходных переменных (сигналов) контроллера.Универсум – по сути, область определения нечеткого множества.

Другой проблемой, достойной обсуждения, является вопрос о том, должна ли быть функция принадлежности непрерывной или дискретной. Непрерывная функция принадлежности определена на непрерывном универсуме значений входа/выхода. Дискретная функция принадлежности определена в рамках вектора с конечным числом элементов. В последнем случае необходимо установить (выбрать) диапазон универсума и значения в каждой его дискретной точке. Выбор между малым или большим разрешением (шагом квантования по уровню) есть компромисс между требованиями точности, быстродействия и пространства, занимаемого на мониторе. Если квантователь затрачивает много времени на выполнение предписанных ему функций и обусловленное этим обстоятельством время задержки имеет большое значение, надо использовать непрерывные функции принадлежности, т.е. надо отказаться от применения квантователя. Лучший путь для использования всего диапазона универсума применить масштабирование входов/выходов. Если вход контроллера содержит лишь один терм, то с помощью выбора масштабирующего коэффициента можно добиться использования в процессе работы всего диапазона универсума. Преимущество такого подхода состоит в том, что он позволяет использовать стандартный универсум, что исключает необходимость добавления новых термов.

Выбор функций принадлежности. Напомним, что каждый элемент универсума является в то же время элементом нечеткого множества с некоторой степенью, может быть даже нулевой. Степени принадлежности, заданные для всех элементов нечеткого множества, полностью описывают нечеткое множество, например, такое, как Отр. Элементам нечетких множеств присваивают степени принадлежности так, чтобы переход от членства (принадлежности) к не членству (не принадлежности) был скорее постепенным, чем скачкообразным. Совокупность элементов с ненулевой степенью принадлежности называют опорой для нечеткого множества. Функция, которая ставит в соответствие каждому элементу универсума определенное числовое значение, называется функцией принадлежности . Проектировщик системы неизбежно сталкивается с вопросом как построить (выбрать) терм-множество. При этом в сущности надо ответить на два вопроса: 1) Какой вид должны иметь функции принадлежности термов? 2) Какое число термов является необходимым и достаточным? Например, лингвистическая переменная ошибка применительно к контроллеру использует семейство термов (терм-множество) Отр, Нуль и Пол. Согласно теории нечетких множеств выбор формы и числа терм является субъективным решением, другими словами, определяется опытом и интуицией проектировщика, однако в любом случае применимы следующие эмпирические правила.

• Число термов должно быть достаточно большим, чтобы допустить присутствие шума в измерениях.

• Желательно иметь некоторое число пересечений (перекрытий) функций принадлежности термов; иначе контроллер может не получить достаточного объема информации, необходимого для формирования эффективного управляющего воздействия.

Предварительный ответ на вопросы (1) и (2) звучит так: необходимое и достаточное число элементов терм-множества зависит от ширины основания (опоры) функций принадлежности термов и наоборот. Один из возможных путей решения данной задачи – опрос операторов технологического процесса (объекта управления) с целью учесть их мнение при выборе кривых для функций принадлежности терм. Хотя следует сказать, что операторы обычно также затрудняются с ответом на вопрос о требуемом виде кривых для функций принадлежности.

Н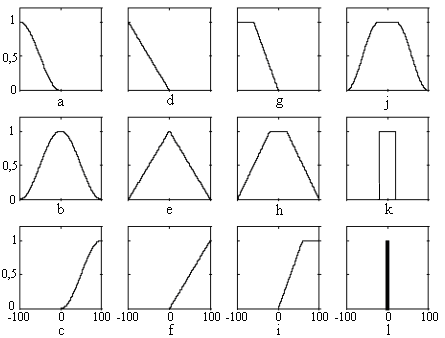 екоторые авторы рекомендуют следующий подход.Начать конструирование с треугольных функций принадлежности. Все функции принадлежности (ФП) для конкретных входов/ выходов должны быть симметричными треугольниками одной и той же ширины (одного и того же основания) вида (e). Крайние левая и правая ФП должны быть функциями вида (d) и (f) (рис. 2.7).

П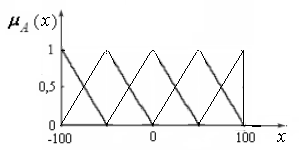 ерекрытие ФП между собой должно составлять не менее 50 %. Ширина (основание) треугольников должно быть выбрано так, чтобы каждое значение универсума было членом (элементом) по меньшей мере, двух множеств, исключая, пожалуй, элементы на самых концах диапазона (см. рисунок ниже). С другой стороны, надо отметить, что если имеется разрыв между соседними ФП, ни одно из правил не работает при всех значениях входа/выхода, принадлежащих этому разрыву. Следовательно, контроллер не знает, что ему делать. На рис. 2.7 приведены примеры некоторых типичных функций принадлежности. Читая сверху вниз, слева направо: (a) s - функция, (b) - функция, (с) z - функция, (d–f) различные версии треугольной функции, (g–i) различные версии трапецеидальной функции, (j) - функция с плоской вершиной, (k) прямоугольная функция, (l) синглтон. ФП могут быть с плоскими вершинами, кусочно-линейными и треугольной формы, или наклонными с горизонтальными уступами вида (g) и (i). Речь выше шла о выборе функций принадлежности для условий (антецедентов). Теперь обратимся к выбору функций принадлежности для заключений (консеквентов).Напомним, что нечеткое множество представляет собой набор упорядоченных пар (2.5). Здесь элемент x принадлежит универсуму и есть его степень принадлежности к множеству . Отдельно взятая пара называется нечетким синглтоном, другими словами, одноточечным множеством или множеством, состоящим из одного элемента. Использование в качестве выходного сигнала контроллера синглтона (singleton output) означает, что нечеткое множество в консеквенте (заключении) правил заменяется четким числом (скаляром), например, так.1. Если ошибка есть Пол, то выход равен 10 вольтам. Модель, описываемая правилами, подобными (2.5,а), называют синглтонной моделью.

Использование в качестве выхода синглтона обладает следующими достоинствами:

• упрощаются вычислительные операции;

• можно свести весь диапазон значений управляющего сигнала к крайним значениям этого диапазона;

• такое решение может быть актуальным как интуитивный путь написания правил.