Несколько входов (многомерная лингвистическая модель)

В случае если контроллер имеет один выход y и r входов x₁, x₂,…,x_r, т.е., если каждая часть «Если» N правил Если x₁ есть A_1i и x₂ есть A_2i и … x_r есть A_ri , то y есть B_i, содержит r переменных, матрица отношения для дискретных универсумов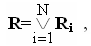

где , обобщается (расширяется) в (r+1) – й массив. Здесь , ,…, , соответственно функции принадлежности термов A_1i, A_2i ,…, A_ri, B_i. Для вычисления матрицы отношения R надо осуществить дискретизацию универсумов входов и выхода. Кроме того, для последующей инференции следует запомнить значения элементов этой матрицы. Поэтому говорят о матрице R как о массиве, используя терминологию языков программирования, и тем самым, подразумевая, что для вызова ее элементов надо указать r+1 индекс.

Пусть (i=1,…,r) будут действительными входами (синглтонная фаззификация), тогда инференция выполняется с помощью обобщенной композиции

.

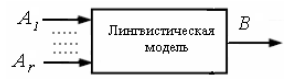Инференция продолжает оставаться все той же операцией композиции; мы должны лишь следить за размерностью. При этом правила описывают лингвистическую нечеткую модель с r входами и одним выходом B, называемую многомерной лингвистической моделью, представленной с помощью отношений

Выводы. Мы пришли к методу представления и выполнения одного правила

Если уровень есть НИЗКИЙ, то сигнал (V1) есть ОТКРЫТЬ

в компьютерной программе. Этот метод в кратком изложении выглядит так.

1. Определить функции принадлежности низкий и открыть нечетких множеств НИЗКИЙ и ОТКРЫТЬ, соответствующие низкому уровню и открытию вентиля; они могут быть определены на различных универсумах.

2. Представить импликацию как отношение R с помощью внешнего произведения R = низкий min открыть. В результате получаем матрицу.

3. Осуществить инференцию с фактическим измерением. В самом общем случае это измерение есть нечеткое множество, скажем, НЕ ОЧЕНЬ НИЗКИЙ уровень с функцией принадлежности не очень низкий. Функция принадлежности v₁ для управляющего воздействия находится посредством композиционного правила инференции,

v₁ = не очень низкий R .

15. Перенос пар-в ПИД-ра в нечеткий НПД+И-контроллер

Если цель управления заключается в стабилизации управляемой величины на заданном уровне, то естественно рассматривать ошибку управления в качестве входного сигнала для нечеткого контроллера, и отсюда вытекает мысль о том, что и производная и интеграл от ошибки управления также могут быть использованы как входные сигналы для такого контроллера. Однако при настройке нечеткого ПИД-контроллера трудно судить о влиянии каждого из его параметров (коэффициентов усиления) на такие показатели качества, как перерегулирование, длительность переходного процесса, в силу того, что этот контроллер в большинстве случаев обладает ярко выраженными нелинейными свойствами, и, кроме того, имеет большое число настраиваемых параметров. В этом разделе предлагается процедура, позволяющая трансформировать технологию выбора параметров в области ПИД- регуляторов в область нечетких контроллеров. Основная идея заключается в том, чтобы, начав проектирование с настройки обычного (четкого) ПИД-регулятора, заменить его эквивалентным линейным нечетким контроллером, затем преобразовать линейный контроллер в нелинейный нечеткий контроллер, и, в конечном счете, настроить должным образом последний контроллер. Описанный здесь подход уместен, если ПИД-регулятор в принципе может быть использован в целях управления данным объектом или уже применяется. Систематическая процедура настройки, сопровождающая такой подход, упрощает выбор параметров нечеткого контроллера и может служить мостом на пути автонастройки последнего.

Перенос параметров ПИД-регулятора в нечеткий контроллер

Т ретий шаг в процедуре проектирования нечетких контроллеров − перенести параметры ПИД-регулятора в линейный нечеткий контроллер. Входом нечеткого ПИД-контроллера являются три входных сигнала: ошибка, интеграл ошибки и производная ошибки, а выходом управляющий сигнал (рис. 1). В отличие от четкого ПИД- регулятора нечеткий ПИД- контроллер имеет четыре коэффициента усиления: по ошибке KE, по производной ошибки KCE,по интегралу ошибки KIE, по выходу KU. Функция f описывает преобразование вход-выход нечеткого ПИД-контроллера. Однако базовые правила с тремя входами просто написать, но они получаются весьма пространными, и, кроме того, правила, содержащие в качестве входов интеграл ошибки, могут быть причиной неприятностей, связанных с «залипанием интегратора». Поэтому обычно осуществляют автономное (отдельное) от правил вычисление интегральной составляющей, так что нечеткий ПИД-контроллер проектируют как параллельное соединение нечеткого ПД-контроллера и интегратора, т.е. нечеткий ПД+И (НПД+И) контроллер. Выход нечеткого ПД-контроллера в общем случае есть нелинейная функция ошибки и скорости изменения ошибки, U₁(t)=f(KE*e(t),KCE*ce(t)). (3). Снова функция f является отображением связи вход-выход, но уже нечеткого ПД-контроллера, и на этот раз ей соответствует графическое отображение в виде поверхности управления.

Т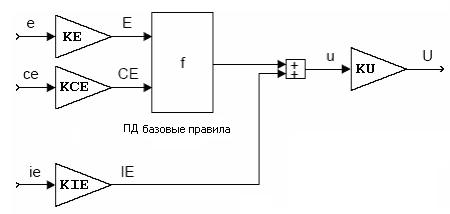 аким образом, выход нечеткого ПИД- контроллера является функцией трех входов . (4)

Линейная аппроксимация (4) имеет вид

(5)

.

В последнем выражении мы предполагаем, что коэффициент усиления не равен нулю. Из сравнения (2) и (5) получаем соотношения, связывающие коэффициенты усиления (параметры) четкого и линейного нечеткого ПИД-контроллеров =K_p , (6) =T_d ,(7) . (8). Полученный контроллер обладает всеми достоинствами ПИД управления, но также не лишен неблагоприятных эффектов, связанных с резкими скачками производной и залипанием интегратора. НПД+И контроллер имеет одну дополнительную степень свободы, т.к. он имеет на один коэффициент усиления больше, чем четкий ПИД-регулятор. Эта степень свободы используется, чтобы задействовать полный диапазон универсума одного из входных сигналов. Свободным параметром должен быть KE или KCE в зависимости от того, какой из этих коэффициентов после умножения на них соответственно e(t) и приводит к наибольшему входному сигналу. Качество системы зависит от вида поверхности управления. При линейной поверхности управления нечеткий контроллер может быть сделан полностью аналогичным по своему действию четкому ПИД-регулятору. В целом ряде случаев нелинейная поверхность управления может обеспечить более высокое качество управления, чем классическое ПИД управление. Однако это зависит от свойств объекта управления и от того, насколько продуманно выбран вид нелинейной поверхности управления. Т.к. в частном случае нечеткий ПИД-контроллер является эквивалентным четкому ПИД-регулрегулятору, можно утверждать, что его свойства, по крайней мере, будут не хуже последнего. УдобУдобно при настройке системы управления начать с классического ПИД-регулятора и постепостепенно преобразовать его в нечеткий контроллер.

Выводы. В нечетком контроллере входной сигнал проходит через блок предварительной обработки (препроцессор), статический нечеткий преобразователь и блок окончательной обработки (постпроцессор). Предварительная обработка включает в себя масштабирование (линейное или нелинейное), дискретизацию, а также квантование по уровню в случае квантования (векторизации) функций принадлежности термов. Если же квантование по уровню не используется, то вид функций принадлежности соответствует первоначально выбранному. Когда конструируются базовые правила, проектировщик должен решить вопросы, касающиеся числа используемых термов, формы их функций принадлежности и диапазонов перекрытия этих функций принадлежности между собой. Сами правила должны бытьнаписаны проектировщиком системы, правда, лишь тогда, когда нецелесообразно или нет возможности применить для этой цели такие средства, как самоорганизация или искусственные нейронные сети. При реализации правил возможен выбор между операциями минимизации и алгебраического произведения для осуществления активизации. Имеется также выбор, касающийся метода дефаззификации; центр тяжести, вероятно, является наиболее широко используемым. Окончательная обработка включает в себя масштабирование выхода.