1.Коньюнкция условий и разбиение пространства входа.

б) Нечеткий контроллер описывается N правилами.

Если используется набор (множество) из N нечетких правил типа Если-То,

Если ошибка e есть и скорость изменения ошибки ce есть , То управление u есть _i , , (2.28a),то находим нечеткие выводы по каждому правилу и затем образуем результат, т. е. нечеткий вывод по всему множеству правил как логическую сумму выводов (заключений), полученных по каждому правил ,(2.29),

где ,(2.29,а) является нечетким выводом по i-му правилу. Сама операция (2.29) называется агрегированием выводов или аккумуляцией выводов.В свою очередь значение , , (2.29,б)представляет собой степень истинности утверждения «нечеткое множество близко к множеству » или, другими словами, степень выполнения предпосылки i-го правила. Весь алгоритм максиминной инференции графически иллюстрируется для N=2 на рис. 2.7,б.

Если e и ce – четкие (количественные переменные) соответственно e’ и ce’, так что имеет место (2.27), то

, ,

так что , . (2.29,б)

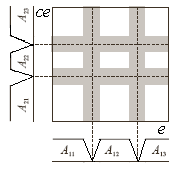
Разбиение пространства входов. Набор правил в форме конъюнкции условий (предпосылок), т. е. в форме (2.29,а) или (2.29,б), разделяет (разбивает) пространство входов (пространство условий) на решетку из областей (боксов), параллельных осям e и ce . Такое разбиение называется решетчатым разбиением. Каждый бокс является пересечением соответствующих терм. Рис. 2.7,в

Это показано на рис. 2.7,в в случае трех терм-множеств для каждой из переменных e и ce, имеющих трапециидальные функции принадлежности, причем используются N=9 правил. Кажется, можно ограничиться лишь тремя правилами. Однако тогда только три бокса, расположенные по диагонали, не смогут охватить все пространство входов (плоскость e,ce). Для того, чтобы накрыть все пространство входов, необходимо добавить еще 6 правил, комбинируя между собой все термы переменных e и ce. На рис. 2.7,в слева функции принадлежностей терм не пересекаются, и каждый бокс соответствует своему правилу, другими словами, своему значению . Светлые участки на боксах определяются значениями =1, а серые – значениями .На рис. 2.7,в справа функции принадлежности терм пересекаются (перекрываются) и здесь серые участки как раз определяются этими пересечениями. Отсюда серые участки принадлежат одновременно двум и более правилам, следовательно, отражают для таких правил значения меньшие единицы. Если термами множества являются q (обычно q<N) синглтонов с ФП (2.30)

то нечеткий вывод (заключение) по всему множеству из N правил, иначе ФП множества , определяется выражением 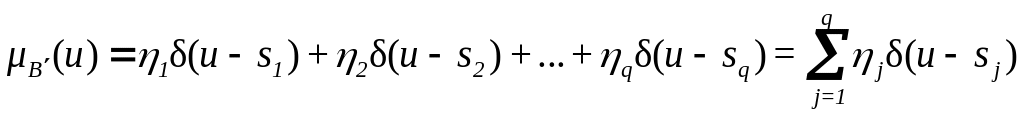, (2.31) где величина определяет возбуждающую силу j -го синглтона. Здесь представляет собой элемент подмножества всех степеней истинности из множества степеней истинности правил, которые соответствуют j-му синглтону (терму выхода со значением ). Дело в том, что при q < N несколько правил содержат в части То один и тот же синглтон.

2. Нечеткие множества. Универсум, функция принадлежности Традиционные (общепринятые, четкие) множества. Множество есть любая совокупность элементов (предметов) произвольной природы, которые можно трактовать как единое целое. Кантор описывал множество посредством его членов так, что отдельные предметы из данного универсума (окружающего мира) являются его (множества) членами или нет. Понятия множества, совокупности, класса, так же как понятия предмет, элемент, член являются синонимами. Вообще любое нечто, названное в обыденном разговоре множеством является множеством и в математическом смысле (сравните следующие примеры).

Пример 1.1 (множества). Следующие списки или совокупности предметов хорошо определены, что дает право назвать их множествами:а) множество неотрицательных чисел меньших чем 4. Это конечное множество с четырьмя элементами 0, 1, 2 и 3;б) множество живых динозавров в подвалах Палеонтологического музея в г. Москве. Это множество не содержит ни одного элемента и поэтому называется пустым множеством;в) множество числовых результатов измерения напряжения, превышающих 10 вольт. Хотя это множество является бесконечным множеством, однако нетрудно ответить на вопрос является ли результат данного измерения напряжения его элементом или нет.

Множество можно определить, перечисляя его элементы. Эти элементы полностью характеризуют множество. Список элементов A={0,1,2,3} полностью определяет конечное множество (конечное число элементов). Нельзя перечислить все элементы бесконечного множества. Поэтому мы должны вместо списка указать некоторое свойство, присущее всем элементам множества, например, используя предикат (утверждение) x>10. Такое множество определяется элементами из окружающего мира, для которых утверждение является истинным. Таким образом, имеются два пути описания множества: явно с помощью списка либо неявно с помощью предиката. Классическое (четкое) множество имеет четкие границы. Так классическое множество A, фигурирующее в примере в) может быть выражено как ,что ясно, недвусмысленно говорит о граничном значении, равном 10. При этом , если x меньше, чем это число, то x принадлежит множеству A, в противном случае x не принадлежит этому множеству.

Нечеткие множества. Следуя идеям Заде, заметим, что многие множества для определения своих элементов требуют другие критерии (границы), чем один критерий вида или-или (напряжение или меньше или больше 10 вольт). Заде предложил использовать понятие степень принадлежности, чтобы переход от «принадлежности элемента к множеству» к «непринадлежности элемента множеству» был нерезким, а постепенным, плавным, т.е. границы нечеткого множества, что следует из его названия являются нечеткими, размытыми. При этом степень принадлежности, заданная для всех его элементов, называется функцией принадлежности и описывает полностью нечеткое множество. Степень принадлежности конкретного элемента множества представляет собой обычно положительное вещественное число, расположенное в диапазоне от 0 до 1 и часто обозначаемое греческой буквой . Чем больше такое число, тем больше степень принадлежности. Заде рассматривал множество Кантора как особый случай, при котором все элементы множества A имеют полную степень принадлежности =1, а те, которые не принадлежат множеству, имеют степень принадлежности, равную нулю, т.е. . При этом функция принадлежности такого множества A определяется как 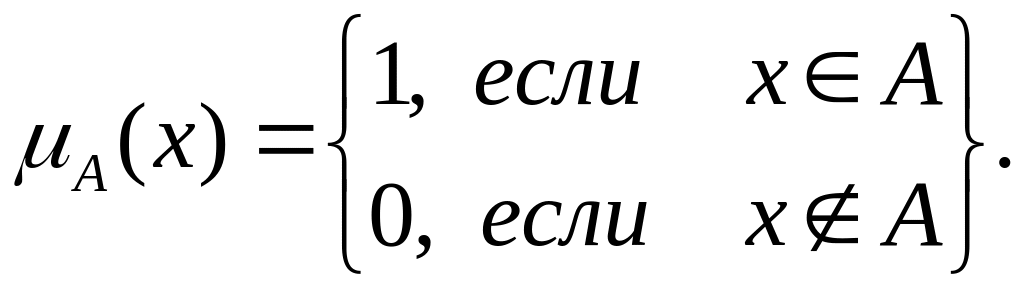Он назвал, между прочим, множество Кантора ненечетким; в настоящее время для такого названия используется термин четкое множество, что позволяет избежать некоторых дилемм (затруднительных положений). Заметим, что Заде не дал формальной основы для определения степени принадлежности. Степень принадлежности 50- летнего человека к множеству молодой человек зависит от собственной точки зрения. Степень принадлежности является определенным числом, однако, субъективной мерой, зависящей от ситуации (окружающей обстановки) и обстоятельств.

Функция принадлежности отличается от функции распределения вероятностей в связи с тем, что лингвистическая (словесная) неопределенность имеет другую природу по сравнению со статистической неопределенностью. Проиллюстрируем это положение с помощью примера с числом съедаемых яиц.

Пример 1.2 (Вероятность относительно возможности). Рассмотрим утверждение «Борис съедает за завтраком X яиц», где .Мы можем найти плотность вероятности распределения p такого события, фиксируя число съеденных Борисом яиц в течение 100 дней:

U = [ 1 2 3 4 5 6 7 8 ], p = [ 0,1 0,8 0,1 0 0 0 0 0 ].

Нечеткое множество, выражающее степень легкости, с которой Борис съедает за завтраком X яиц, может быть представлено следующей так называемой возможностью распределения ,

U = [ 1 2 3 4 5 6 7 8 ], = [ 1 1 1 1 0,8 0,6 0,4 0,2 ].

Как видим, для X =3 (съесть 3 яйца) возможность равна 1, а вероятность лишь 0,1.

Пример показывает, что возможность события не является тем же, что его вероятность. Однако, если событие возможно, оно должно быть и вероятным.

Универсум

Э лементы нечеткого множества выбираются (черпаются) из универсального множества или короче универсума. Универсум включает в себя все элементы, которые можно использовать при рассмотрении множества. Можно сказать, что универсум является областью определения множества, следовательно, и его функции принадлежности. Тем не менее, универсум зависит от контекста, как показывает следующий пример.Пример 1.3 (универсум). а) множество «молодые люди» может иметь в качестве универсума всех людей, проживающих на земле. Как альтернативу универсумом можно считать людей, возраст которых лежит между 0 и 100 годами; эти люди будут представлять переменную возраст (рис. 1.3). Множества более или менее молодой, очень молодой и не очень молодой получены из множеств молодой и старый; Применение универсума позволяет исключить из рассмотрения ошибочные результаты измерений, например отрицательные значения для уровня воды в баке.

В том случае, когда мы имеем дело с нечисловыми переменными, например, с переменной вкус пищи, которые не могут быть измерены в отношении численного масштаба, мы не можем использовать в качестве универсума множество чисел. При этом элементы универсума должны быть взяты, как говорят, из психологического континуума; для данного примера таким универсумом может быть {горький, соленый, кислый, сладкий,…}.Определение (нечеткое множество). Если U набор элементов, обозначаемых традиционно x, то нечеткое множество A в U определяется как упорядоченное множество пар: ,где называется функцией принадлежности (ФП) x к A. Функции принадлежности

Каждый элемент в универсуме является членом (элементом) нечеткого множества A с некоторой степенью принадлежности, может быть и с нулевой. Четкое множество элементов, имеющих отличную от нуля степень принадлежности, называют основным (опорным) для нечеткого множества или носителем нечеткого множества. Функция, которая каждому элементу универсума ставит в соответствие определенное число, называется функцией принадлежности . Если =0,8, то говорят, что элемент x_i на 80% принадлежит нечеткому множеству A. Нечеткое множество строго определяется с помощью функции принадлежности, другими словами, логика определения понятия нечеткого множества не содержит никакой нечеткости. Четкое множество является частным случаем нечеткого множества, т.е. понятие нечеткого множества является расширенным понятием, охватывающим понятие четкого множества.

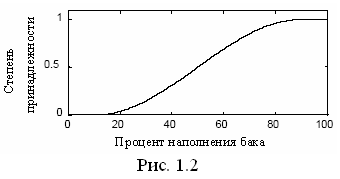
Непрерывное и дискретное представления. Существуют два альтернативных представления функций принадлежности в компьютере: непрерывный и дискретный. В непрерывной форме функция принадлежности есть математическая функция, возможно программа. Функция принадлежности может быть колоколообразной (так называемая - кривая), s-образной (называемая s-кривой), обратная s-образной (называемая z-кривой), треугольной или трапециидальной. На рис. 1.2 изображена как пример - кривая. В дискретной форме функция принадлежности и универсум представляют собой дискретные значения (точки) в списке (векторе). В ряде случаев удобно иметь дело с дискретными представлениями.В соответствии с эмпирическим правилом непрерывная форма требует более быстродействующего, но с меньшей памятью АЦП, чем дискретная форма.