
- •1.Кинематика прямолинейного движения точки
- •2.Кинематика Криволинейного движения точки и Движения твердого тела
- •3.Кинематика вращательного движения
- •4.Динамика материальной точки
- •5.Силы в механике
- •6.Импульс системы
- •7.Работа, мощность, энергия
- •8.Момент силы,момент импульса. Сила приложенная к твердому телу, которое может вращаться вокруг некоторой точки, создает момент силы. Действие момента силы аналогично действию пары сил.
- •9.Уравнение динамики вращат. Движения
- •10.Свободное вращение твердого тела.
- •11.Кинематическая энергия сложного движения.Упругий и неупругий удар.
- •12.Элементы статики. Центр масс.
- •13.Механическая модель идеального газа.
- •14.Уравнение Клапейрона-Менделеева.Изопроцессы.
- •15.Распределение молекул идеального газа по скоростям.
- •16.Основное уравнение мкт.
6.Импульс системы
Импульс системы материальных точек под действием внешних сил изменяется. Согласно второму закону Ньютона, скорость изменения импульса равна равнодействующей внешних сил:
|
|
(3.1) |
Система
материальных точек, на которую не
действуют внешние силы, или действие
внешних сил скомпенсировано,
называется замкнутой.
В этом случае уравнение принимает вид ![]() ,
и, следовательно, импульс системы при
движении не изменяется со временем:
,
и, следовательно, импульс системы при
движении не изменяется со временем: ![]() .
Таким образом, если
геометрическая сумма внешних сил,
действующих на систему материальных
точек, равна нулю, то импульс системы
сохраняется, то есть не меняется со
временем. При
этом импульсы отдельных частиц замкнутой
системы могут меняться со временем.
Однако эти изменения всегда происходят
так, что приращение импульса одной части
системы равно убыли импульса оставшейся
части системы. Другими словами, отдельные
части замкнутой системы могут только
обмениваться импульсами.
.
Таким образом, если
геометрическая сумма внешних сил,
действующих на систему материальных
точек, равна нулю, то импульс системы
сохраняется, то есть не меняется со
временем. При
этом импульсы отдельных частиц замкнутой
системы могут меняться со временем.
Однако эти изменения всегда происходят
так, что приращение импульса одной части
системы равно убыли импульса оставшейся
части системы. Другими словами, отдельные
части замкнутой системы могут только
обмениваться импульсами.
Центр масс— геометрическая точка, характеризующая движение тела или системы частиц как целого.
Положение
центра масс системы материальных
точек
определяется следующим образом:
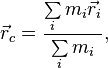
где ![]() — радиус-вектор центра
масс,
— радиус-вектор центра
масс, ![]() —
радиус-вектор i-й
точки системы,
—
радиус-вектор i-й
точки системы, ![]() — масса i-й
точки.
— масса i-й
точки.
Под реактивным понимают движение тела, возникающее при отделении некоторой его части с определенной скоростью относительно тела. При этом возникает т.н. реактивная сила, сообщающая телу ускорение.
Уравнение Мещерского — основное уравнение в механике тел переменной массы, полученное И. В. Мещерским в 1897 году[1] для материальной точки переменной массы (состава).
Уравнение обычно записывается в следующем виде:
![]()
где:
 —
масса материальной
точки переменной массы
—
масса материальной
точки переменной массы —
скорость движения материальной
точки переменной массы;
—
скорость движения материальной
точки переменной массы;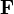 —
внешние силы, действующие
на материальную
точку переменной массы
—
внешние силы, действующие
на материальную
точку переменной массы —
относительная скорость
присоединяющихся частиц;
—
относительная скорость
присоединяющихся частиц; —
относительная скорость
отделяющихся частиц;
—
относительная скорость
отделяющихся частиц;
7.Работа, мощность, энергия
Элементарной работой силы называется скалярное произведение
 ,
,
где
 - бесконечно малое перемещение точки
приложения силы.
- бесконечно малое перемещение точки
приложения силы.
Работа при перемещении из точки 1 в точку 2 определяется интегрированием по траектории:
 .
.
Если на частицу действуют одновременно несколько сил, то работа результирующей силы равна сумме работ каждой из действующих сил.
Если работа силы не зависит от траектории, а определяется только начальным и конечным положениями материальной точки, то такая сила называется консервативной (или потенциальной).
Силы, не удовлетворяющие этому условию, называют диссипативными. Таковой является сила трения.
Средняя мощность силы за время t:
 ,
где А – работа силы за это время.
,
где А – работа силы за это время.
Мгновенная
мощность
 ,
где
- мгновенная скорость.
,
где
- мгновенная скорость.
Кинетическая энергия материальной точки массы m, движущейся со скоростью v:
Ек= .
.
Теорема о кинетической энергии: изменение кинетической энергии частицы равно суммарной работе А всех сил, действующих на частицу:
 .
.
Изменение потенциальной энергии U частицы в поле консервативной силы:
 ,
,
где Аполя – работа силы поля.
Связь между силой и потенциальной энергией частицы:
 ,
,
 .
.
Изменение полной механической энергии Е=Ек+U частицы в поле в поле консервативных сил:
Е2 – Е1=Астор.,
где Астор. – работа сторонних (то есть не принадлежащих к данному полю) сил.
Единицы измерения работы и энергии в СИ – Джоуль(Дж).
