9 Тарау

9-1. Келесі жағдайлардағы:

(а) р_х = 0,96 – х-ң барлық мәндері үшін және і = 0,09

(б) l_x = 1000(1-х/115) және і = 0,13,

40 жастағы адамға сатылған, номинал сомасы 100 000 өмірлік сақтандыру полисінің бағасын анықтаңыз.

Шешуі:

(а)

(б)

9-3. Келесі жағдайлардағы:

(а) р_х = 0,96 – х-ң барлық мәндері үшін және і = 0,09

(б) l_x = 1000(1-х/115) және і = 0,13,

40 жастағы адамға сатылған, номинал сомасы 100 000 мерзімі 30 жылдық сақтандыру полисінің бағасын анықтаңыз.

Шешуі:

(а)

(б)

9-4. Келесі жағдайлардағы:

(а) р_х = 0,96 – х-ң барлық мәндері үшін және і = 0,09

(б) l_x = 1000(1-х/115) және і = 0,13,

40 жастағы адамға сатылған, номинал сомасы 100 000 өмір сүру мерзімі 30 жылға дейінгі сақтандыру полисінің бағасын анықтаңыз.

Шешуі:

(а)

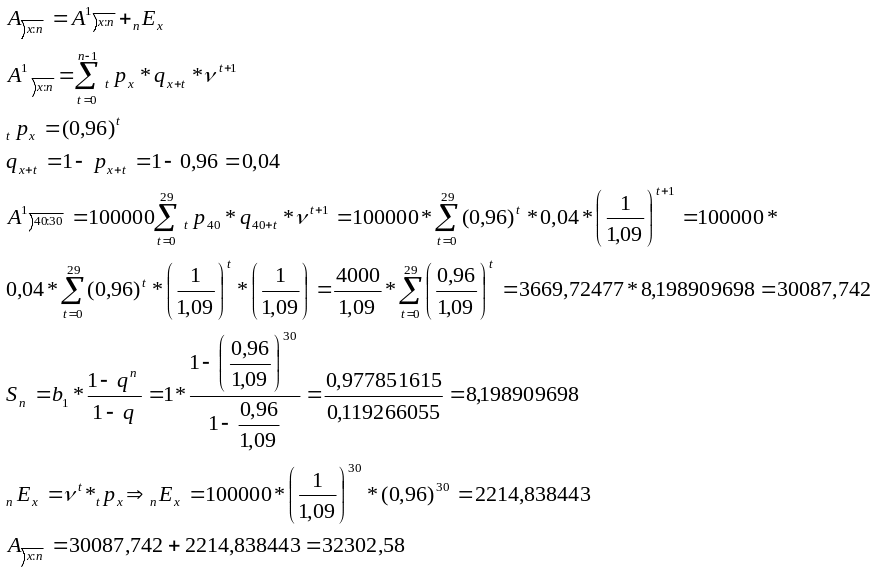
(б)

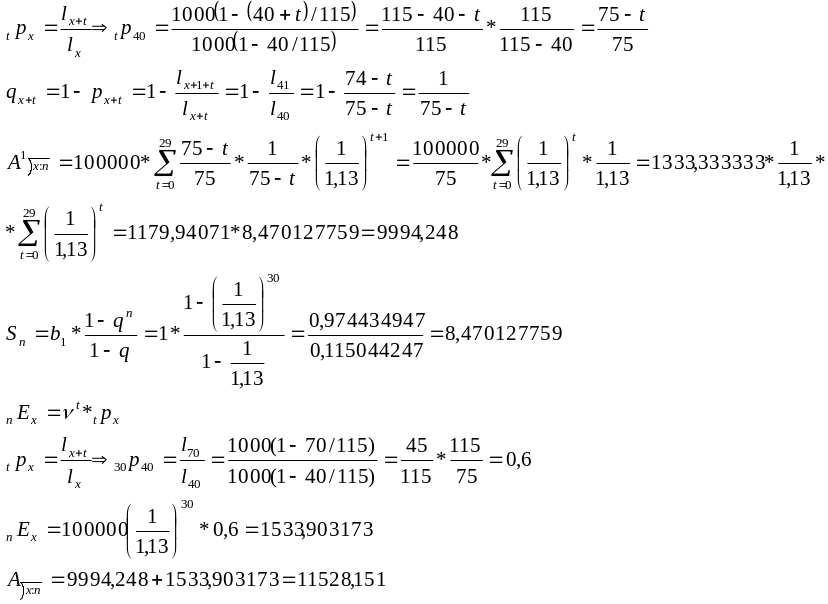
9-5. Адамның жасы 40-та және полистің алғашқы 30 жылдағы номиналдық құны 100000. Егер сақтандырылған адам 70 жасқа дейін жетсе, 70000 төленеді. Ал қалған 30000 өмір бойы сақтандыру полисі арқылы төленеді.

а) р_х = 0,96 х-тің барлық мәні үшін және i=0,09

б) l_x = 1000*(1-x/115) және i=0,13

Шешуі: a) PV = A_30:40 + * (70000 + 30000A₇₀)

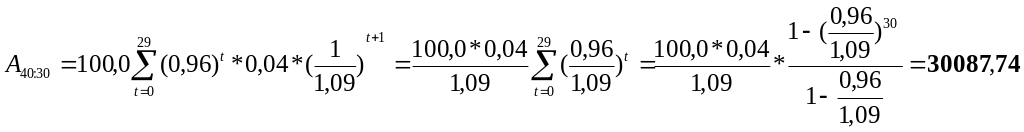
PV = 30087,74 + * (70000 + 9230,77) = 31842,57

б) PV = A_30:40 + * (70000 + 30000A₇₀)

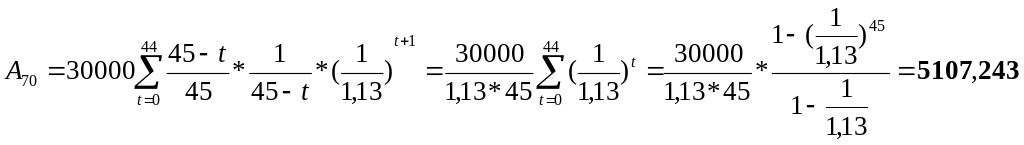
PV = 9994,2 + * (70000 + 5107,243) = 11150,78

9-18. Герман мөлшері 100 000 өмірлік сақтандыру полисін 45 жаста сатып алады. Егер:

(а)

(б) ,

болса, бірмерзімді нетто−премияны анықтаңыз.

Шешуі:

(а)

(б)

9-20. 30 жастағы адам сатып алған келесі полис үшін бірмерзімді нетто-премияны коммутациялық функциялар арқылы белгілеңіздер: 50000, егер өлім алғашқы 20 жылда болса; 100000, егер өлім келесі 20 жылда болса; және 10 жыл мерзімге өмір сүруді сақтандыру 50000 көлемінде.

Шешеуі:

9-22 а ) пайыздық қойылымды табыңыз, егер: а_х = 15,5 А_х = 0,25

А_х = 1 – d = 1 – d*(1+ а_х)

0,25 = 1 – 16,5 график подбора → i = 0,0476

б) D_x+1 табыңыз, егер: M_x = 3000, M_x+1 = 2800 q_x = 0,01

C_x = M_x - M_x+1 = 3000 – 2800 = 200

C_x = d_x ν^x+1 → d_x = l_x – l_x+1 → (l_x – l_x+1)*ν^x+1 = l_x ν^x+1 - l_x+1ν^x+1 → * ν^x+1 - D_x+1 → - D_x+1

C_x = - D_x+1 200 = 20000 - D_x+1

D_x+1 = 19800

9-23. Рональд 40 жасында өмір бойына сақтандыру полисін иеленеді. Бұл полис бойынша алғашқы 10 жылда ,ҒҒҒ10000, келесі 10 жылда 20000 төленеді. Егер Рональд 60 жасқа дейін өмір сүрсе, онда ол өмірінің соңына дейін әрбір айдың аяғында 200 алып отырады.

Егер M₄₀ = 750, M₅₀ = 600, M₆₀ = 420, D₄₀ = 4500, D₆₀ = 1100, N₆₀ = 10000 болса, нетто сыйақыны табыңыз.

Шешуі:

9-24. Анжела 55 жаста бірінші төлем 65 жаста төленетін, жылына мөлшері 4000 қалдырылған сақтандыру аннуитетін сатып алады. Егер ол 65 жасқа жетпесе, өлім болғаннан кейінгі жылдың соңында сома мөлшері 10000 төленеді. Егер болса, осы сақтандыру полисі үшін бірмерзімді нетто-премияны анықтаңыз.

Шешуі:

26. а) 40 жастағы адамның өлім кезінде төленетін 50000 мөлшердегі өмірді сақтандыру полисінің нетто сыйақысын табыңыз, егер: i = 0,06 және _tp₄₀ = (0,96)^t t-ның барлық мәні үшін;

б) а пунктін тағы да шығарыңыз, егер адам өмір бойы сақтандырудың орнына 30 жыл мерзімге сақтандыру полисін сатып алса;

в) а пунктін тағы да шығарыңыз, егер адам өмір бойы сақтандырудың орнына 30 жыл мерзімге страхование на дожитие сатып алса;

Шешуі:

а)

б)

в)

26. а) 40 жастағы адамның өлім кезінде төленетін 100000 мөлшердегі өмірді сақтандыру полисінің құнын табыңыз, егер: δ = 0,05 және μ_х = 0,04 х-тің барлық мәні үшін;

б) а пунктін тағы да шығарыңыз, егер адам өмір бойы сақтандырудың орнына 30 жыл мерзімге сақтандыру полисін сатып алса;

в) а пунктін тағы да шығарыңыз, егер адам өмір бойы сақтандырудың орнына 30 жыл мерзімге страхование на дожитие сатып алса;

Шешуі:

а) ν = е^-0,05 _tp₄₀ = е^-0,04t

б)

в)

9-30. Өлім кезінде төленетін 200000 мөлшердегі өмірді сақтандыру полисінің нетто сыйақысы 70000-ға тең. Егер өлім күші μ_х = 0,03, ал δ константа, яғни тұрақты сан болса, 200000 мөлшердегі 5 жылға кейінге қалдырылған өмірді сақтандыру полисінің нетто сыйақысын есептеңіз.

Шешуі:

μ_х = 0,03 _tp_x = e^-0,03t ν = e^-δt

9-40. Тим 50 жасында өмір бойы сақтандыру полисін сатып алады. Алғашқы сақтандыру төлемі 20000 және одан әрі 5000-ға өсіп отырады. Нетто сыйақыны табыңыз, егер: D₅₀ = 500, R₅₀ = 2300, M₅₀ = 220.

Шешуі:

51: 20000 = 15000 + 1*5000

52: 25000 = 15000 + 2*5000

……………………………..

9-41. Тим 50 жасында 20 жыл мерзімге сақтандыру полисін сатып алады. Алғашқы сақтандыру төлемі 20000 және одан әрі 5000-ға өсіп отырады. Нетто сыйақыны табыңыз, егер: D₅₀ = 500, R₅₀ = 2300, M₅₀ = 220, M₇₀ = 60, R₇₀ = 400.

Шешуі:

51: 20000 = 15000 + 1*5000

52: 25000 = 15000 + 2*5000

……………………………..

70: 115000 = 15000 + 20*5000

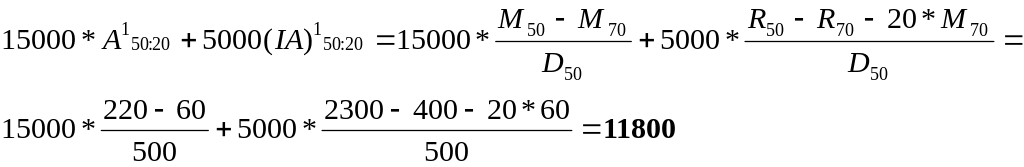
9-42. Тим 50 жасында 20 жыл мерзімге сақтандыру полисін сатып алады. Алғашқы сақтандыру төлемі 20000 және одан әрі 5000-ға өсіп отырады. 70 жасына дейін өседі де, ал одан кейін 120000-ның деңгейінде тұрақты болып қалады. Нетто сыйақыны табыңыз, егер: D₅₀ = 500, R₅₀ = 2300, M₅₀ = 220, M₇₀ = 60, R₇₀ = 400.

51: 20000 = 15000 + 1*5000

52: 25000 = 15000 + 2*5000

……………………………..

70: 115000 = 15000 + 20*5000

71: 120000 = 15000 + 21*5000

72: 120000: 15000 + 22*5000 = 125000

9-49. Рой 50 жасында 10000 мөлшерде өмірді сақтандыру полисін сатып алады. Ол бұл полисті жыл сайынғы төлемдер арқылы төлейді. Осы төлемдерді анықтаңыз.

а) М₅₀ = 150, N₅₀ = 2200

б) М₅₀ = 150, i = 0,04 және D₅₀ = 220

в) М₅₀ = 150, N₅₀ = 2200, D₅₀ = 220 төлемдер ай сайын төленеді.

Шешуі:

а) Р* = 10000А₅₀

б) Р* = 10000А₅₀

в) 12Р* = 10000А₅₀

9-50. 45 жастағы адам 10000 мөлшерде 20 жыл мерзімге өмірді сақтандыру полисін сатып алады. Алғашқы төлем Х, осыдан кейінгі әрбір жылы 2Х. Х-ты анықтаңыз.

а) М₄₅ = 800, М₆₅ = 520, N₄₅ = 25000, N₆₅ = 5500, D₄₅ = 1200

б) N₄₅ = 25000, D₄₅ = 1200, N₆₅ = 5500, D₆₅ = 400, i = 0,03

Шешуі:

45: х а)

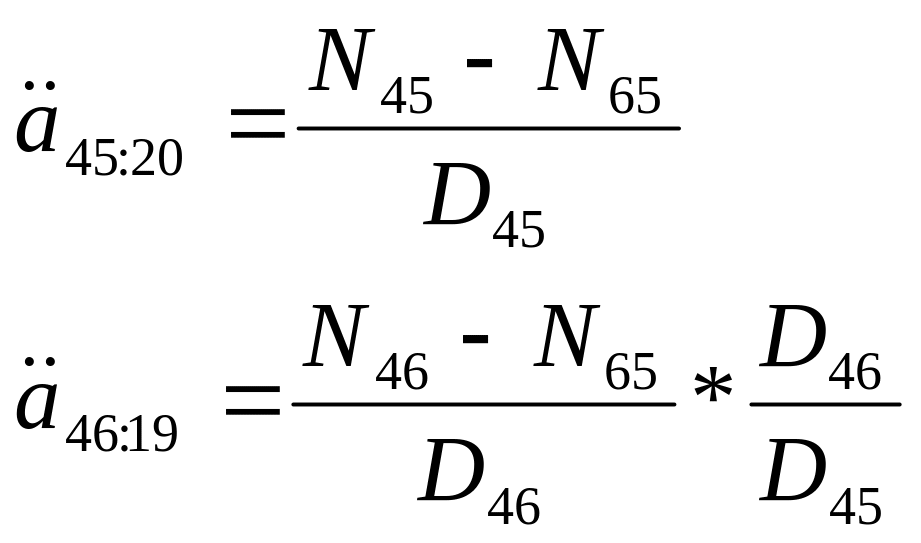
46: х + х N₄₆ = N₄₅ – D₄₅ = 25000 – 1200 = 23800

…………

65: х + х

б) M_x = D_x – d*N_x

M₄₅ = D₄₅ – d*N₄₅ = 1200 – i/1+i * 25000 = 1200 – 0,029*25000 = 471,8446602

M₆₅ = D₆₅ – d*N₆₅ = 400 – i/1+i * 5500 = 400 – 0,029*5500 = 239,8058252

9-56. 25 жастағы адам 100000 мөлшерде өмірді сақтандыру полисін сатып алады. Сыйақы өмір бойына әр жылдың басында төленеді, ал сақтандыру төлемі өлген жылдың соңында төленеді. Осы полиспен байланысты шығындар мынадай: 1-ші жылы 60% брутто-сыйақы, 2-ші мен 5-ші жылы 20% брутто-сыйақы, одан кейін әр жыл сайын 10% брутто-сыйақы. Жыл сайынғы брутто-сыйақы анықтаңыз,

егер: N₂₅ = 120000, N₂₆ = 112000, N₃₀ = 96000, i = 0,06.

Шешуі: 1-ж 2-ж 3-ж 4-ж 5-ж 6-ж .........

60% 20% 20% 20% 20% 10% 10% ……..

9-9 – мысал. 30 жастағы адамның сатып алған өлім мезетінде төленетін мөлшері 100000 өмірлік сақтандыру полисінің бірмерзімді нетто-премиясын анықтаңыз, егер барлық t мәндері үшін.

Шешуі:

9-10 – мысал. 30 жастағы адамның сатып алған өлім мезетінде төленетін мөлшері 100000 өмір сүру мерзімі 20 жылдық сақтандыру полисінің бірмерзімді нетто-премиясын анықтаңыз, егер барлық t мәндері үшін.

Шешуі:

11-тарау

11-1. Мэри 15 жаста, ал Хелен мен Гарри – 25 жастағы егіздер. Әр келесі ықтималдықтарды анықтаңыздар:

(а) үшеуі де әлі 40 жыл өмір сүретіндігінің ықтималдығы;

(б) кем дегенде біреуі 40 жыл өмір сүрмеуінің ықтималдығы;

(в) ең көп дегенде біреуі 40 жыл өмір сүрмеуінің ықтималдығы;

(г) Мэри 50 жасқа жетеді, сол кездегі егіздердің біреуінің тағы 20 жыл өмір сүруінің ықтималдығы.

Шешуі:

(а)

(б)

(в) (г)

11-7. 65 жастағы Фрэнсис ол да, күйеуі (60 жастағы) де тірі болған жағдайда ғана, әр жылдың соңында 1000 төленетін сақтандыру аннуитетін сатып алады. Осы аннуитет үшін бірмерзімді нетто-премияны анықтаңыздар, егер

Шешуі:

11-8. 65 жастағы Фрэнсис ол да, күйеуі (60 жастағы) де тірі болған жағдайда ғана, әр жылдың басында 1000 төленетін сақтандыру аннуитетін сатып алады. Осы аннуитет үшін бірмерзімді нетто-премияны анықтаңыздар, егер

Шешуі:

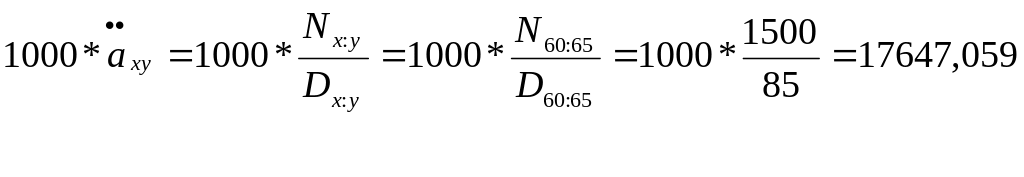
11-9. 65 жастағы Фрэнсис ол да, күйеуі (60 жастағы) де тірі болған жағдайда ғана, әр жылдың басында 1000 төленетін сақтандыру аннуитетін сатып алады. Осы аннуитет үшін бірмерзімді нетто-премияны анықтаңыздар, егер алғашқы үш төлем кепілді болса және .

Шешуі:

11-10. Айталық, берілген адамдар тобы үшін қысқартылған өмір сүру ұзақтығы n-ге тең, егер топ n жыл өмір сүрсе, бірақ n+1 емес (топ құрамы n жыл ішінде өзгермейді, бірақ n+1 жылдан кейін өзгереді). Егер болса, жұптың (ху) бірге өмір сүруінің қысқартылған ұзақтығы 1-ге тең кездегі ықтималдықты табыңыздар.

Шешуі: яғни жұптың екі емес бір жыл өмір сүруін анықтауымыз керек,

11-14. Жулио үшін өмір сүру ықтималдығы 1≤t≤4 үшін теңдеуімен сипатталады, ал Гарольд үшін өмір сүру ықтималдығы 1≤t≤5 үшін теңдеуімен сипатталады. Егер, і=0,07 болса, біреуі ғана тірі болған кезде ғана, не Джулио, не Гарольд, әр жылдың соңында 1000 көлемінде төленетін аннуитеттің құнын анықтаңыздар.

Шешуі:

11-24. 65 жастағы Пол өзінің өлімінен кейін әйеліне жылына 1000 көлемінде төлемдерді қамтамасыз ететін реверсивті аннуитет сатып алады. Егер болса, осы аннуитет үшін бірмерзімді нетто-премияны анықтаңыздар.

Шешуі:

11-27. 40 жастағы Берта аннуитет сатып алғысы келеді. Оған екі эквивалентті жоспар ұсынылды:

(а) оған өмір бойы ай сайын 500 көлеміндегі төлемдер, ал оның өлімінен кейін оның күйеуіне 300 көлеміндегі төлемдер;

(б) оған өмір бойы ай сайын 600 көлеміндегі төлемдер, ал оның өлімінен кейін оның күйеуіне 150 көлеміндегі төлемдер.

Егер және әр жоспарда бірінші төлем сол мезетте жүзеге асырылатыны белгілі болса, Берта мен оның күйеуінің төлемдерінің ағымдық құнын анықтаңыздар.

Шешуі:

11-28. 40 жастағы Берта аннуитет сатып алғысы келеді. Оған екі эквивалентті жоспар ұсынылды:

(а) оған өмір бойы ай сайын 500 көлеміндегі төлемдер, ал оның өлімінен кейін оның күйеуіне 300 көлеміндегі төлемдер;

(б) оған өмір бойы ай сайын 600 көлеміндегі төлемдер, ал оның өлімінен кейін оның күйеуіне 150 көлеміндегі төлемдер.

Егер және әр жоспарда бірінші төлем сол мезетте жүзеге асырылатыны белгілі болса, әр жағдайдағы күйеуінің төлемдерінің ағымдық құнын анықтаңыздар.

Шешуі:

11-30. 35 жастағы Марсэлла мен 40 жастағы Мария екеуінің біреуі өлгеннен кейін өмір сүретін әйелге жылдық төлемі бар, бірінші төлем өлген жылдың соңында болатын аннуитет сатып алады. Егер бірінші Марсэлла өлсе, онда Мария өмір бойы жыл сайын 2000-нан алып отырады. Егер Мария бірінші өлсе, онда Марсэллаға өмір бойы Х төлемдер төленеді. Полис құны екі әйел тірі болған уақытқа дейін, әр жылдың басында 400 көлеміндегі жыл сайынғы нетто-премия арқылы төленеді. Егер және , Х-ті табыңыздар.

Шешуі:

11-35. Барни 55 жаста, ал Гильда 65 жаста. Аннуитет Барниға өмір бойы әр айдың басында Х көлемді төлемдерді қамтамасыз етеді. Егер Барни Гильдадан бұрын өлсе, онда Гильда реверсивті аннуитет бойынша Х-100 алатын болады. Осы аннуитет үшін бірмерзімді нетто-премия 50000-ға тең. Х-ті табыңыздар, егер

Шешуі:

11-36. 60 жастағы Этель айына 80 көлемінде төлемі бар, бірінші төлем аннуитет сатып алысымен жүзеге асырылатын аннуитет сатып алды. Оның өлімінен кейін күйеуі, қазіргі уақытта 65 жастағы, 50 көлемінде ай сайын төлемдер алып отырады. Егер оның күйеуі Этельден ерте өлсе, онда Этельдің төлемдері айына 100-ге дейін артады. Осы аннуитет үшін бірмерзімді нетто-премияны табыңыздар, егер

Шешуі:

11-37. 65 жастағы Уолли өзі және 60 жасар әйелі тірі болғанға дейін айына 400 көлемінде төлемдерді қарастыратын, бірінші төлем аннуитет сатып алысымен жүзеге асырылатын аннуитет сатып алады. Егер екеуінің біреуі өлсе, онда тірі қалғанның төлемі 300-ге дейін төмендейд. Осы аннуитет үшін бірмерзімді нетто-премияны анықтаңыздар, егер

Шешуі:

12-тарау

12-1. 20 жастағы Полин 60 жаста зейнетақыға шығады, және оның зейнетақысы айына 4000 құрайды. Егер D₂₀ = 2800, N₆₀ = 7500, N₆₁ = 7000, барлық болашақ төлемдердің ағымдық құнын анықтаңыздар. Бірінші төлем зейнетақыға шыққан мезетте төленеді деп есептелген.

Шешуі:

12-2. 20 жастағы Полин 60 жаста зейнетақыға шығады, және оның зейнетақысы жылына 48000 құрайды. Егер D₂₀ = 2800, N₆₀ = 7500, барлық болашақ төлемдердің ағымдық құнын анықтаңыздар. Бірінші төлем зейнетақыға шыққан мезетте төленеді деп есептелген.

Шешуі:

12-3. 20 жастағы Полин 60 жаста зейнетақыға шығады, және оның зейнетақысы жылына 48000 құрайды. Егер D₂₀ = 2800, N₆₁ = 7000, барлық болашақ төлемдердің ағымдық құнын анықтаңыздар. Бірінші төлем зейнетақыға шыққан мезеттен кейін бір жылдан соң төленеді деп есептелген.

Шешуі:

12-4. 20 жастағы Полин 60 жаста зейнетақыға шығады, және оның зейнетақысы айына 4000 құрайды. Егер D₂₀ = 2800, N₆₀ = 7500, N₆₁ = 7000, барлық болашақ төлемдердің ағымдық құнын анықтаңыздар. Бірінші төлем зейнетақыға шыққан мезеттен кейін бір айдан соң төленеді деп есептелген.

Шешуі:

12-7. Мигельдің зейнетақы жоспары 1999 жылдың 31-қаңтарынан бастап 15 жыл бойы айына 1000 көлемде кепілдендірілген төлемдерді құрайды. Зейнетақы төлемдерінің жартысын оның компаниясы қаржыландырады, ал қалған жартысы зейнетақы жоспары бойынша жинақтаушы шотпен қаржыландырылады, ол 1989 жылдың 31-наурызынан бастап 10 жыл бойы квартал сайынғы төлемдерден құралады. Мигель зейнатқыға шығу мезетіне дейін өмір сүреді деп болжамданады. Егер i=0,06, бекітілген салымдармен зейнетақы жоспары бойынша квартал сайынғы төлемдердің көлемін табыңыздар.

Шешуі:

12-1 мысал. 45 жастағы Франциско үлкен мұнау компаниясына жұмыс жасайды. Ол 65 жасында зейнетке шығады және өмірбойы жыл сайын 20000зейнетақы алатын болады. Бірінші төлем зейнетке шыққаннан кейінгі 1-жылы. Францисконың болашақ төлемдерінің ағымдағы құнын табыңдар, егер

Шешуі:

12-2 мысал. 45 жастағы Франциско үлкен мұнау компаниясына жұмыс жасайды. Ол 65 жасында зейнетке шығады және өмірбойы квартал сайын 5000 зейнетақы алатын болады. Бірінші төлем зейнетке шыққаннан кейін 3 айдан соң төленеді. Францисконың болашақ төлемдерінің ағымдағы құнын табыңдар, егер ,

Шешуі:

12-3 мысал. Әр жылдың соңында Ванданың жұмыс берушісі зейнетақы қорына оның еңбекақысының 10%-н салып тұрады. Ванданың еңбекақысы жыл сайын 5%-ға өсіп отырады, ал зейнетақы қорының табыстылығы жылына 9%. Егер Ванданың қазіргі еңбекақысы жылына 20000 болса, онда қорда 15 салымнан кейін қандай сома жинақталады, егер Ванда осы уақыт аралығына дейін өмір сүреді және сол компанияда көрсетілген уақытта жұмыс жасайды деп болжамданса.

Шешуі:

12-4 мысал. 2000 жылдың 1 қаңтарында зейнетақы қорының нарықтық құны 3000000-ға бағаланған. 2000 жылдың 31 наурызында қорға қосымша 160000 мөлшердегі сома қосылды. Жарна қосылғаннан кейін оның нарықтық құны 3300000-ға бағаланды. 2000 жылдың 31 тамызында 12000-ға тең бір жолғы төлем жасалды. Осыдан кейінгі активтер құны 3250000-ға бағаланды. 2000 жылдың 31 желтоқсанында активтердің нарықтық құны 3500000-ға тең болды.

А) 2000 жылға мөлшері бойынша өлшенген табыстылық қойылымын табыңыз. Жыл ұзақтығы 1 жылдан төмен аралық үшін пайыздардың жай түрі қоладынлады деп болжамданады.

Б) 2000 жылға уақыт бойынша өлшенген табыстылық қойылымын табыңыз.

Шешуі:

А)

Б)

.

.

.