3 Тарау

3-1. Келесі прогрессиялардың әрбіреуінен 17-ші мүшесі мен алғашқы 11 қосындысын табыңыз.

а) ариф/қ прогр. 2, 7, 12, 17,..... d=5 a=2 17: a+16d=2+16*5=82

S₁₁=n/2*[2a+(n-1)d] = 11/2*[4+50]=297

г) геом/қ прогр. 5, 15, 45,…… r=3 a=5 17: ar¹⁶ = 5*43046721=215233605

S₁₁ = a(1-r¹¹ )/(1-r)=442865

3-5. Альфонс банктегі шотына 1977 жылдан бастап 20 жыл бойы әрбір жылдың басында 450 тг салады. Егер i=0,08 болса, 1996 жылдың соңында оның шотында қанша ақша бар.

Шешуі:

S₂₀ =

3-6. Аннуитет бойынша жылына 1000 бірлік 8 жыл бойы төленеді. Егер i=0,08 болса, келесілерді есептеңіз:

А) Аннуитеттің алғашқы төлемнен 1 жыл бұрынғы құнын;

Б) Аннуитеттің соңғы төлемнен 1 жылдан кейінгі құнын;

В) Аннуитеттің 5-ші төлем кезіндегі құнын;

Г) Аннуитеттің ағымдағы құны екі еселенуі үшін аннуитеттің мерзімі қандай

Шешуі:

А) PV(0) = 5746,64

Б) PV(9) = 11487,56

В) PV(5) = PV(9)*ν⁴ = 8443,70

Г) PV(0)*2 = 11493,28 = 1000*а_n = 0,9194624 = 1- νⁿ n = 32,731

3-18. Аннуитет 25 жыл бойы мына түрде төленеді: алғашқы 10 жылда әр жылдың аяғында 500 төленеді, ал қалған 15 жылда әр жылдың аяғында 300 төленеді. Егер i=0,08% болса, бірінші төлемнен үш жыл бұрынғы (за три года до первого платежа) аннуитеттің құнын есептеңіз.

Шешуі:

A₁₀₊₁₅ = 500* + ν¹⁰300* =4544,449136

4544,449136*(1+i)^-2 = 3896,13

3-21. Бір адам біраз зейнетақы жинақтау үшін депозитке 25 жыл бойы әр жылдың басында 2500 салып тұрады. Соңғы салым салынған жылдың соңынан бастап, салған ақшасын 20 жыл бойы алып отырады. Осы алынатын соманы есептеңіз. Егер алғашқы 25 жылда i=0,07, одан кейін i=0,11 болса.

Шешуі:

158122,5943 = Х*а₂₀

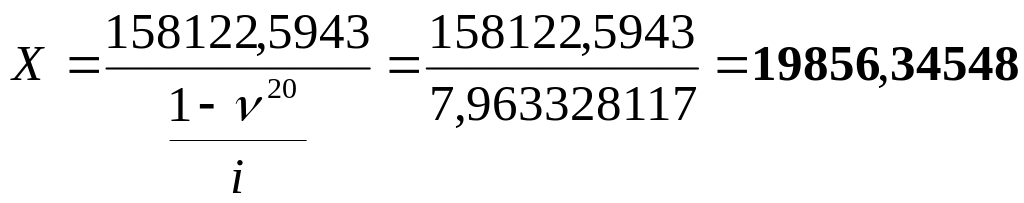
3-25. Альберт Гловерге мынадай контрактар ұсынады:

а) 5 жыл бойы әр жылдың аяғында 3200000;

б) 5 жыл бойы әр жылдың басында 3000000;

в) 10 жыл бойы әр жылдың аяғында 1800000

Егер i=0,04 болса, осы контрактардың жылдың басындағы құнын анықтаңыз

Шешуі:

а) PV(0) = 3200000*a₅ = 14245831,46

б) PV(0) = 3000000* a₅ *(1+i) = 13889685,67

в) PV(0) = 1800000* a₁₀ = 14599612,4

3-34. 25000 көлеміндегі ссуда 20 жыл бойы әр жылдың аяғында жылдық төлемдермен өтелуі тиіс. Алғашқы 5 жылда төлемдер k, келесі 5 жылда 2k, келесі 5 жылда 3k, келесі 5 жылда 4k. k табыңыз, егер i=0,12

Шешуі:

25000 = ka₅ + ν⁵ 2ka₅ + ν¹⁰ 3ka₅ + ν¹⁵ 4ka₅ = ka₅ (1 + ν⁵ 2 + ν¹⁰ 3 + ν¹⁵ 4)

25000 = k3,604776202 (1 + 1,1345371 + 0,730785045 + 0,965919708)

25000 = k 13,8119076

k = 1810,03

3-37. Жұмысшыға 10 жыл бойына медициналық шығындар үшін 20000 көлемінде төлемдер мен келесі 20 жыл бойына сақтандыру төлемдеріне құқығы төленеді. Медициналық шығындар үшін төлемдер жедел (немедленно) басталады, ал сақтандыру төлемдері 1 жылдан кейін басталады. Сақтандыру компаниясы мұндай төлемдерді төлеу үшін 680000 көлемінде қор құрды. Егер i=0,07 болса, жыл сайын төленетін сақтандыру төлемін анықтаңыз.

Шешуі:

680000 = 20000*а₁₀*(1+0,07) + Х*а₂₀

529695,355 = Х*10,59401425 Х = 49999,5

3-41. 25 жыл бойы әр жылдың аяғында 1000 көлемінде депозит салынады. Соңғы депозит салынғаннан 5 жылдан кейін жыл сайынғы төлемдер басталады және шексіз жалғасады. Осы төлемдерді табыңыз, егер i=0,09.

Шешуі:

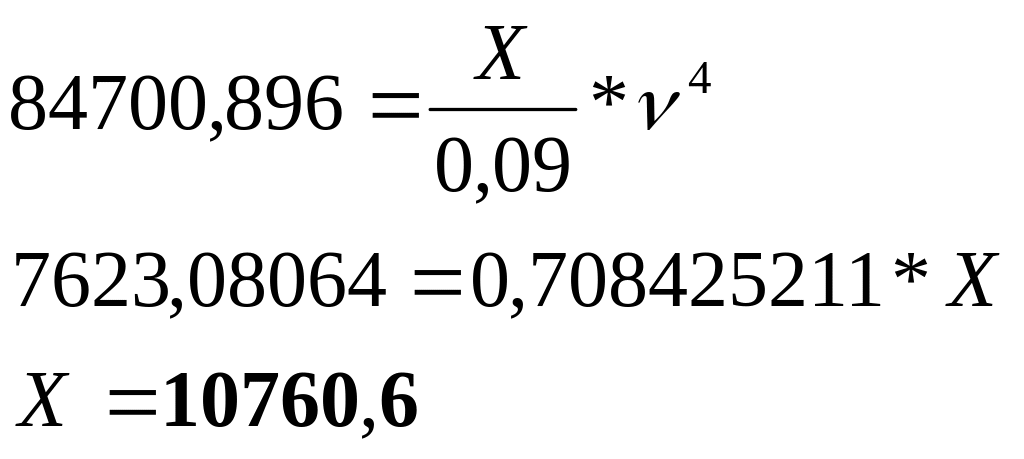
3-44. Альберт Гловер «Blue Jays» командасымен келісім шарт жасасады: 5 жыл бойы әр жылдың басында олар Гловерге 3 000 000 төлеулері тиіс. Гловер өзінің зейнетақысын қамтамасыз ету мақсатында жыл сайынғы еңбекақысының бір бөлігін қорға салып отырады. Қор оған жыл сайын шексіз периодта 400 000 төлеп тұрады, бірінші төлем соңғы еңбекақысын алған жылдан 1 жылдан кейін басталады. Егер i=0,08 болса, жыл сайын Гловерде еңбекақысының қанша бөлігі өзінде қалады?

Шешуі:

400000/0,08 = 5 000 000

3-47. Джоан жергілікті банктен 6000 көлемінде ссуда алады. Ол бұл соманы жыл сайын 800 көлемінде белгілі бір мерзімде өтегісі келеді және 800-ден аз соңғы төлем бар. Бірінші төлем 1 жылдан кейін басталады. Егер i=0,11 болса, қажетті төлем санын және соңғы төлемді табыңыз.

Шешуі:

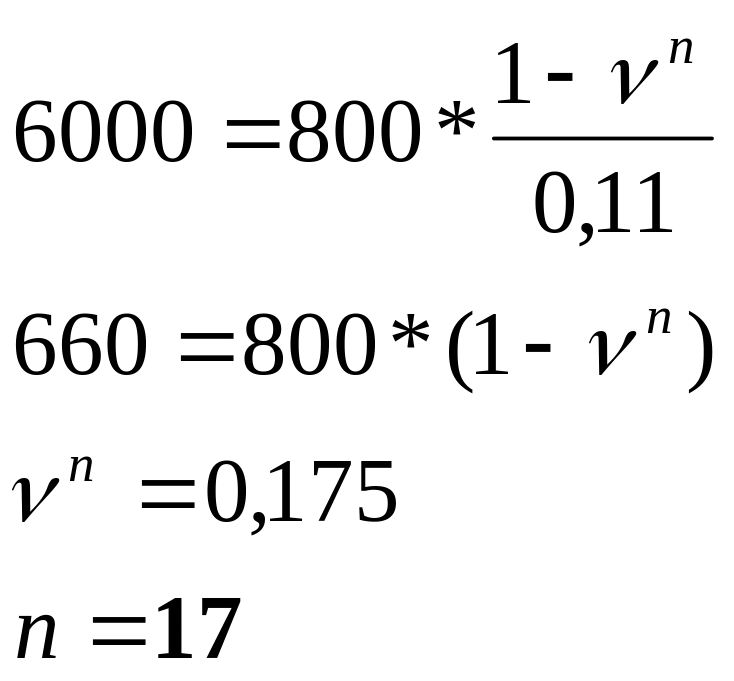
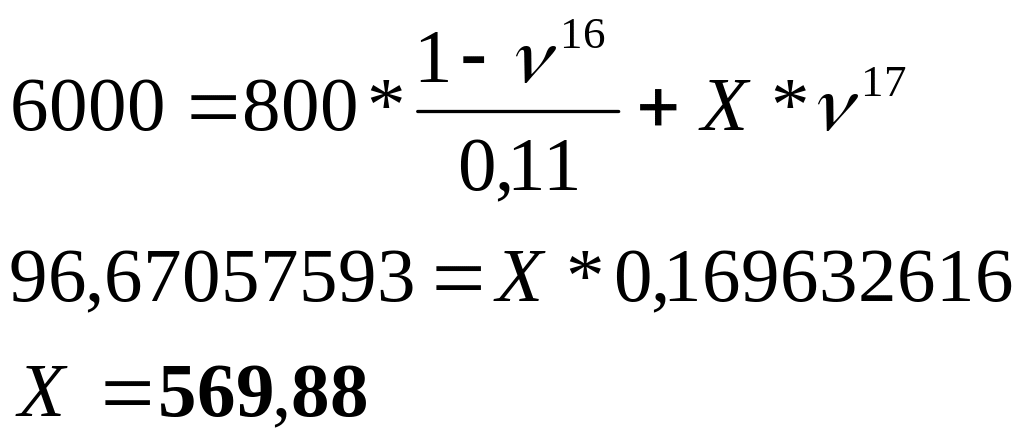
3-51. 3 жыл бойы әр айдың соңында 200 төлеп тұрады. 6500 ссуданы өтеу үшін тиімді айлық пайыздық қойылым қанша болу керек.

Шешуі:

«подбор параметра» шығарамыз