1 Тарау
1-1. 1995 жылдың 1 қаңтарындағы жағдай бойынша Альфонстың шотында 14000 бар.
а) Жай пайыздар ставкасын жылдық 8% деп алып, 2001 жылдың 1 қаңтарына жинақталған соманы табыңыз.
б) Күрделі пайыздар ставкасын жылдық 8% деп алып, 2001 жылдың 1 қаңтарына жинақталған соманы табыңыз.
в) Нақты жай пайыздар ставкасын жылдық 8% деп алып, 1995 жылдың 8 наурызына жинақталған соманы табыңыз.
г) Күрделі пайыздар ставкасын жылдық 8% деп алып, бірақ уақыттық моменттер арасында сызықтық интерполяция орын алады деп есептеп, 1997 жылдың 15 ақпанына жинақталған соманы табыңыз.
Шешуі:
а) а(t) = 14000*(1+0,08*6) = 20720
б) а(t) = 14000*(1+0,08)6 = 22216,24
в) а(t) = 14000*(1 + 66/365*0,08) = 14202,52
г) а(2) = 14000*(1+0,08)2 = 16329,6
а(3) = 14000*(1+0,08)3= 17635,968
а(3) – а(2) = 17635,968 – 16329,6 = 1306,368
47/365 * 1306,368 = 168,23 + 16329,6 = 16497,82
1-7. а) Қанша жылдан кейін 1000 бірлік 1400-ға дейін өседі, егер жылдық жай пайыздар ставкасы 12% болса.
б) Қандай жай пайыз ставкасы кезінде 1000 бірлік 6 жылдан кейін 1500-ға өседі?
в) а және б пунктерінің тапсырмасын жай пайыздар орнына күрделі пайыздар пайдаланып қайталаңыз.
Шешуі:
а) 1400 = 1000*(1+0,12t) б) 1500 = 1000*(1+i6) в) 1400 = 1000*(1+0,12)t
1+0,12t = 1,4 i6 = 0,5 1,12t = 1,4
t = 3,3 i = 0,08 t = log 1,4/log 1,12 = 2,96899
1500 = 1000*(1+i)6
i = 0,06991
1-10. Күрделі пайыздардың жылдық ставксы 1994 жылы 13%, 1995 жылы 11%, 1996 жылы 15%-ды құрады. 3 жыл мерзімінде сәйкес табыс әкелетін күрделі пайыздардың жылдық тиімді ставкасын есептеңіз.
Шешуі:
Мысалы 1000 тг салсақ,
1000*(1+0,13) = 1130
1130*(1+0,11) = 1254,3 1442,445 = 1000*(1+i)3
1254,3*(1+0,15) = 1442,445 (1+i)3 = 1,442445
1+i = 1,12988
i = 0,12988
1-14. 1995 жылдың 1 қаңтарында Мэридің шотында 14000 бар.
а) Егер күрделі пайыздар жылдық 12%-ды құраса, 1989 жылдың 1 қаңтарындағы ағымдық құнын табыңыз.
б) Егер күрделі дисконт жылдық 12%-ды құраса, 1989 жылдың 1 қаңтарындағы ағымдық құнын табыңыз.
Шешуі:
а)
б) d = 0,12 i = d/1-d = 1,12/0,88 = 0,136
1-23. 100 бірлік 6 айдан кейін 107 бірлікке өседі. Келесілерді табыңыз:
а)
б) i(2)
в) i
г) d(3)
Шешуі:
а)
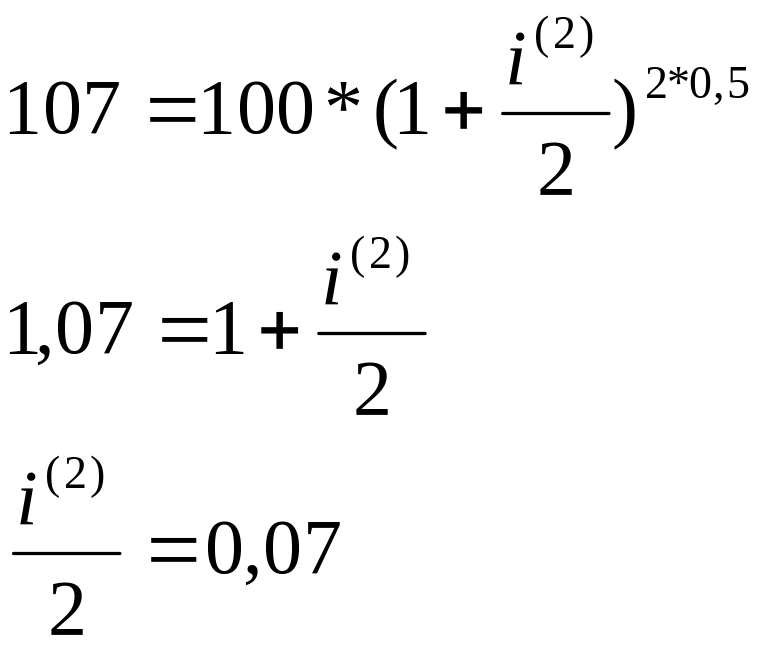б) i(2)
= 2*0,07 = 0,14
в)
г)
1-29. Келесі жағдайларда δ баламалы мағынасын табыңыз.
а) i=0,13 б) d=0,13 в) i(4) = 0,13 г) d(5) = 0,13
Шешуі:
а) еδ
= 1+i
б)
еδ
= 1+i = 1/1-d
в)
еδ
= 1+i =
г) еδ
=
еδ = 1,13 еδ = 1,149425287 еδ = 1,136475928 еδ = 1,140788713
δ = 0,12222 δ = 0,13926 δ = 0,12793 δ = 0,13172
1.2-мысал. Джек 1996 жылдың 1-қаңтарында 15 % жай пайыздық қойылыммен банктен 1000 ақша бірлігі ссудасын алды. 1996 жылдың 17-қаңтарында ол банкке қанша ақша сомасын қайтаруы тиіс?
Шешуі: t уақыт мезетіндегі соманы анықтау үшін A(t) = 1000(1+0,15t) формауласын қолданамыз. бірақ қазіргі жағдайда формулаға t-ң қандай мәнін қоямыз деген мәселе туындап отыр. Осындай есептеулерді жүргізу үшін келесідей әдістер қолданылады:
а) бірінші әдіс нақты жай пайыздар әдісі. Мұнда
формуласы
қолданылады. Біздің жағдайда
.
Джек
тең соманы қарыз болады.
б) екінші
әдіс қарапайым жай пайыздар әдісі
(немесе Банктік ереже) әдісі болып
табылады. Мұнда
.
Біздің жағдайда
.
Осыған сәйкес қарыз
құрайды.
1.3-мысал. Джек жылдық 15 % күрделі пайыздар қойылымы бойынша 1000 ақша бірлігі ссудасын алады.
а) 2 жылдан кейін ол қанша қарыз болады?
б) 57 күннен кейін қанша қарыз болады?
в) 1 жыл 57 күннен кейін қанша қарыз болады?
г) сызықтық интерполияцияны қолдану кезінде 1 жыл 57 күннен кейін қанша қарыз болады?
д) қанша жылдан кейін негізгі сома 2000 бірлікті құрайды?
Шешуі:
(а) 1000(1+0,15)2=1322,50
(б)
болады, сонда жинақталған сома келесідей
.
(в)
.
(г) біз
А(1)=1000*(1+0,15)=1150
және
А(2)=1000*(1+0,15)2=1322,50
аралығында
интерполиациялауымыз керек. Екеуінің
айырмасы А(1)-А(2)=172,50. 57 күнде жинақталатын
бөліктің айырмасы жай пайыздарды
қолданғанда
құрайды. Сонымен 1 жыл 57 күнде жинақталған
құн 1150,00+26,94=1176,94. Байқап қарасақ қарыз
төлеуші осы жағдайда (в)-мен салыстырғанда
артық сома қарыз.
(д) t уақытты келесідей анықтаймыз:
1.4-мысал. 1996 жылдың 1-мамырында Келли жанұясы 93500 ақша бірлігіне жаңа үй сатып алады. 1992 жылдың 1-мамырында осы үйдің бағасы қанша болды? Егер осы кезең аралығында жылжымайтын мүлік бағасы күрделі пайызбен жылына 8 %-ға өсіп отырса.
Шешімі:
0 мезеттегі 93500 сомасынан t=-4 мезетіне
ағымдық құнды анықтаймыз. Ол
тең.
1.5-мысал. 9 % жылдық дисконт қойылымы бойынша 1995 жылдың 1-қаңтарына 1000 ақша бірлігі жинақталу керек.
(а) 1992 жылдың 1-қаңтарына ағымдық құнды анықтау керек.
(б) d-ға сәйкес i-ң мәнін анықтау.
Шешуі:
(а) 1000*(1-0,09)3=753,57.
(б)
.
1.6-мысал. Джейн 1996 жылдың 1-тамызында банктік шотқа 1000 ақша бірлігін салды. Егер жылдық күрделі пайыз қойылымы 7 % болса, 1994 жылдың 1-тамызына осы депозиттің құнын анықтаңдар.
Шешуі:
1.7-мысал. Бір адам 1000 ақша бірлігі көлемінде ссуда алады. Тиімді пайыздық қойылым айына 2 %. 3 жылдан кейін ол қанша қарыз болады.
Шешуі: t=3*12=36 ай.
1000(1+0,02)36=2039,89.
1.8-мысал. Ай сайын есептелетін жылдық 24 % қойылыммен 1000 ақша бірлігінің 3 жылдан кейінгі жинақталған сомасын анықтаңдар.
Шешуі: 24% / 12 = 2 % ай сайын
T=12*3=36
1000(1+0,02)36=2039,89
1.9-мысал. Егер i(6)=0,15 болса, жарты жыл сайын есептелетін эквивалентті номиналды пайыз қойылымын анықтаңдар.
Шешуі:
1.10-мысал. Ай сайын есептелетін номиналды жылдық 12 %-ға эквивалентті жарты жыл сайын есептелетін дисконттың номиналды қойылымын анықтаңдар.
Шешуі:
1.11-мысал. Ссуда 1997 жылдың 23 маусымында алынды. Егер пайыздың интенсивтілігі 14 % болса, келесі мәндерді анықтаңыздар:
(а) ссуданың 2002 жылдың 23 маусымындағы құнын;
(б) і мәнін;
(в) і(12) мәнін.
Шешуі:
(а) 5
жылдан кейінгі құн келесідей: 3000(1+і)5.
(б)
(в)
