14. Теорема о проекциях скоростей двух точек тела:

Определение скоростей точек плоской фигуры (или тела, дви­жущегося плоскопараллельно) связано обычно с довольно сложными расчетами. Однако можно получить ряд других, практически более удобных и простых мето­дов определения скоростей точек фигуры (или тела)

Один из таких методов дает тео­рема: проекции скоростей двух точек твердого тела на ось, проходящую через эти точки, равны друг другу. Рассмотрим какие-нибудь две точки А и В плоской фигуры (или тела). Принимая точку А за полюс (рис.32), получаем . Отсюда, проектируя обе части равенства на ось, направленную по АВ, и учитывая, что вектор 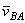 перпендику­лярен АВ, находим и теорема доказана.

15. Мгновенный центр скоростей. Теорема о существовании и единстве м.Ц.С.:

Проекции скоростей двух точек твердого тела на прямую, с оединяющую эти точки, равны между собой:

(1)

Докажем теорему методом от противного. Предположим, что равенство (1) не выполняется и проекции скоростей на прямую AB (рис. 70) не равны между собой. Тогда с течением времени расстояние между точками A и B будет меняться, то есть AB = var, а этого быть не может, так как мы рассматриваем твердое тело. Следовательно, наше предположение не верно, а верно равенство (1), и теорема доказана.

По доказательству мы видим, что теорема не зависит от вида движения тела, главное чтобы тело было твердым.

Мгновенный центр ускорений:

При непоступательном движении плоской фигуры у нее в каждый момент времени имеется точка Q, ускорение которой равно нулю. Эта точка называется мгновенным центром ускорений. Определяется положение центра Q, если известны ускорение   какой-нибудь точки А фигуры и величины  и , следующим путем:

1) находим значение угла , из формулы ;                

2) от точки А под углом , к вектору   проводим прямую АЕ;

при этом прямая АЕ должна быть отклонена от  в сторону вращения фигуры, если вращение является ускоренным, и против вращения, если оно является замедленным, т. е. в сторону направления углового ускорения ;

3) откладываем вдоль линии АЕ отрезок AQ, равный                 

.

16. Определение скоростей точек тела с помощью м.Ц.С.:

Пусть в данный момент t в точке А и В лежащие в сечении S (плоская фигура) имеет v_a и v_В. При чём эти скорости параллельны друг другу, тогда найдём МЦС как точку лежащую на перпендикулярах построенной из точек А и В к этим скоростям. Таким образом положение МЦС найдём зная v_а а так же направление скорости в точки В.

Зная v_а и положение МЦС определим скорость в любой в точке тела.

_АВ= V_A/AP=V_B/AP=V_C/AP

_АВ=

17. Частные случаи определения м.Ц.С:

1. Качение без скольжения плоской фигуры по неподвижной плоскости. В этом случав м.ц.с. (т. Ρ) лежит в точке касания.

2. 

В этом случае м.ц.с. (т. Р) лежит в бесконечности. Величина = 0 и скорости всех точек тела в данный момент равны между собой. Имеем мгновенное поступательное движение:

3 .

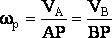
Мгнов-ый центр ск-тей нах-ся в точке пересечения общего перпендикуляра к скоростям и пряной, соединявшей концы векторов скоростей.