49. Работа силы. Мощность:

Величина, характеризующая действие силы на некотором перемещении т-ки наз-ся работой силы. Единица измерения-Дж. Элементарная работа силы = проекции силы на направление точки, умноженной на элементарное перемещение ds. dA= ; dA=F ds cos α=F_τ ds

Если α <90^о, то работа положительная; если α >90^о, то работа А<0; Если α = 90^о, то А=0. Работа силы на любом конечном перемещении S=M₁M₂ определяется интегрированием. А_м1м2= F_xd_x+ F_yd_y+ F_zd_z). Т.о. работа силы на любом перемещении =взятому интегралу вдоль заданного перемещения от элементарной работы сил. Мощностью наз-ся величина, определяющая работу, совершаемую силой за единицу времени. Единица измерения-ватт=1 дж/сек.W=dA/dt, если работа совершается равномерно, то W=A/t.

50. Примеры вычисления работы силы (работа сил тяжести, упругости пружины, трения):

Р абота сил тяжести. Пусть т. М под действием силы тяжести опускается и перемещается от М1 в М2. А(G)=±Gh. Если тело опускается, то работа силы тяжести будет положительная. Если тело подымается, то работа силы тяжести будет отрицательной.

Работа силы упругости. F_упр.=cх. Растянем тело, на него будет действовать сила упругости по з-ну Гука. А(F_упр.) =с(х₀²- х₁²)/2.Работа силы упругости не зависит от траектории, сл., она явл-ся потенциальной. Работа силы трения. Рассмотрим Д-ние тела по некоторой пл-ти под действием активных сил. На данное тело будет действовать сила трения. F_тр.=fN. A (F_тр)= F_тр dS. Работа силы трения не является потенциальной.

51. Теорема об изменении кинетической энергии материальной точки:

Изменение кинетической энергии точки при некотором её перемещении равно алгебраической сумме работ всех действующих на точку сил на том же перемещении.

Выражение теоремы об изменении кинетической энергии материальной точки в дифф. форме: d( )=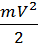

52. Принцип д'Аламбера для материальной точки:

Пусть мы имеем систему, состоящую из n материальных точек. Выделим какую-нибудь из точек системы с массой m_k. Под действием приложенных к ней внешних и внутренних сил F_k ^e и F_kⁱ (в которые входят и активные силы, и р-ции связей) точка получает по отношению к инерциальной системе отсчета некоторое уско­рение w_k.

Введем в рассмотрение величину F_k^и=- m_k w_k

имеющую размерность силы. Векторную величину, равную по модулю произведению массы точки на ее ускорение и направленную проти­воположно этому ускорению, называют силой инерции точки (иногда даламберовой силой инерции).

Тогда оказывается, что движение точки обладает следующим общим свойством: если в каждый момент времени к фактически действующим на точку силам F_k ^e и F_kⁱ прибавить силу инерции F_k^и |то полученная система сил будет уравновешенной, т. е. будет

F_k ^e+ F_kⁱ + F_k^и=0

Это положение выражает принцип Даламбера для одной материальной точки.