40. Две задачи динамики материальной точки. Несвободная материальная точка:

Задачи динамики. Для свободной материальной точки задачами динамики являются следующие: 1) зная закон движения точки, определить действующую на нее силу (первая задача динамики); 2) зная действующие на точку силы, определить закон движения точки (вторая, или основная, задача динамики).

Для несвободной материальной точки, т. е. точки, на которую

наложена связь, вынуждающая ее двигаться по заданной поверх-

поверхности или кривой, первая задача динамики обычно состоит в том, чтобы, зная движение точки и действующие на нее активные силы, определить реакцию связи. Вторая (основная) задача динамики при несвободном движении распадается на две и состоит в том, чтобы, зная действующие на точку активные силы, определить:

а) закон движения точки,

б) реакцию наложенной связи.

41. Динамика прямолинейного дв-ия материальной точки:

Д вижение материальной точки будет прямолинейным, когда действующая на нее сила (или равнодействующая приложенных сил) имеет постоянное направление, а скорость точки в начальный момент времени равна нулю или направлена вдоль силы. Если при прямолинейном движении направить вдоль траектории координатную ось Ох, то движение точки будет определяться первым из уравнений A0), т. е. уравнением называют дифференциальным уравнением прямолинейного движения точки. Иногда его удобнее заменить двумя уравнениями, содержащими первые производные:

42. Динамика криволин-ого дв-ия материальной точки:

В случае криволинейного движения точки основная задача динамики решается с помощью дифференциальных уравнений движения: (1) (2)

(3)

Если задача решается в прямоугольных декартовых координатах, т. е. с помощью уравнений (2), то начальные условия, определяющие положение и скорость точки в начальный момент времени t=0, задаются в виде:

(4)

Проинтегрировав уравнения (2), находят координаты х, у, г движущейся точки, как функции времени t, т. е. определяют закон движения точки. При этом полученные решения будут содержать шесть постоянных интегрирования С1 С2>. . ., С6, значения которых должны определяться по начальным условиям(4)

43. Несвободное движение точки. Уравнение движения точки по заданной неподвижной кривой:

Движение материальной точки будет не свободным, когда в силу наложенных связей, она вынуждена двигаться по заданной поверхности или кривой.

уравнения движения точки по заданной неподвижной кривой

(1)

(2­)

Уравнение(1) не содержит неизвестной реакции N и позволяет непосредственно определить закон движения точки вдоль кривой, т. е. зависимость s=f(t). Уравнения (2) служат для определения реакции связи N.

44. Динамика относ-ого движения точки. Частные случаи:

Относительное движение точки - движение по отношению к неинерциальным, произвольно движущимся по отношению к инерциальной системам отсчета. Рассмотрим точку М, движущуюся под действием сил F1,F2…Fn. Будем изучать движение этой точки по отношению к осям 0xyz, которые движутся относительно инерциальной системы: m ; m + .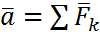

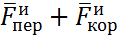Частные случаи:

1)Подвижные оси движутся поступательно: =0 и закон относит.дв-я принемает вид m + .

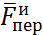2)Подвижн оси перемещаются поступательно, равномерно и прямолинейно:  m инерциальная система отсчета.

3)Точка по отношению к подвижным осям наход в покое: =0, _от= =0 =0, т.к. кориолисово ускорение _от), тогда + =0(уравнение относит равновесия точки)

45. Две меры механического движения. Количество движения и кинетическая энергия материальной точки. Импульс силы: На основании экспериментальных данных Гюйгенс установил, что верной мерой движения является mv 2 и неверной мерой движения является мера движения Декарта mv. Так появились в теоретической физике две меры движения: mv и mv 2, одна из которых применяется в одних случаях, а другая является незаменимой в других случаях. Существование двух мер, которые противоречат друг другу, недопустимо, несмотря на то, что они имеют многочисл-ые эксперим-ые подтверждения. Их обобщение и получение одной общей меры движения стало настоятельной необходимостью. Немецкий математик и философ Лейбниц (1646-1716) меру движения mv 2 вывел прямо из закона свободного падения тел, которому противоречила мера движения mv. Импульс силы. Для характеристики действия, оказывае­мого на тело силой за некоторый промежуток времени, вводится понятие об импульсе силы. Введем сначала понятие об элементарном импульсе, т. е. об импульсе за бесконечно малый промежуток вре­мени dt. Элементарным импульсом силы называется векторная величина dS, равная произведению вектора силы F на элементар­ный промежуток времени dt: dS = Fdt. Направлен элементарный импульс по линии действия силы. Импульс S любой силы F за конечный промежуток времени t_t вычисляется как интегральная сумма соответствующих элементарных импульсов: . Следовательно, импульс силы за любой промежуток времени t₁ равен определенному интегралу от элементарного импульса, взя­тому в пределах от нуля до t₁. В частном случае, если сила F и по модулю, и по напр-ию постоянна (F= const), будем иметь S = Ft₁. Причем, в этом, случае и модуль S = Ft₁. Кол-ом дв-ия точки наз-ся векторная величина mv равная произвед-ию массы точки на вектор её ск-ти. Напр-ен вектор mv так же, как и скорость точки, т. е. по касательной траектории.