1. Кинематика. Кинематика точки. Способы задания движения точки.

2. Скорость точки. Вектор скорости.

3. Ускорение точки. Вектор ускорения.

4. Определение скорости и ускорения точки при координатном способе задания движения.

5. Определение скорости и ускорения точки при естественном способе здания движения.

6. Годограф скорости. Касательное, нормальное, полное ускорение. Естественный тре­угольник. Радиус кривизны.

7. Кинематика твёрдого тела. Виды движения твёрдого тела. Поступательное движение твёрдого тела.

8. Вращательное движение твердого тела. Угловая скорость и угловое ускорение.

9. Равномерное и равнопеременное вращение.

10. Скорости и ускорения точек тела при вращательном движении.

11. Выражения скоростей и ускорений точек тела при вращательном движений в виде век­торных произведений.

12. Плоскопараллельное движение твердого тела. Уравнения плоского движения. Разло­жение плоского движения на поступательное и вращательное.

13. Определение скоростей тела при плоском движении.

14. Теорема о проекциях скоростей двух точек тела.

15. Мгновенный центр скоростей. Теорема о существовании и единственности м.ц.с.

16. Определение скоростей точек тела с помощью м.ц.с.

17. Частные случаи определения м.ц.с.

18. Определение ускорений точек тела при плоском движении.

19. Мгновенный центр ускорений. Определение ускорений точек тела с помощью м. ц. с.

20. Сферическое движение твердого тела. Эйлеровы углы. Уравнения сферического дви­жения.

21. Теорема Эйлера-Даламбера.

22. Мгновенная ось вращения. Мгновенные угловая скорость и угловое ускорение тела при сферическом движении.

23. Скорости точек тела при сферическом движении.

24. Ускорение точек тела при сферическом движении.

25. Формула Пуассона.

26. Общий случай движения свободного твердого тела.

27. Абсолютное, относительное и переносное движение точки.

28. Сложение скоростей при сложном движении точки.

29. Сложение ускорений при сложном движении точки. Случай поступательного пере­носного движения.

30. Теорема Кориолиса. Ускорение Кориолиса.

31. Определение направления и модуля ускорения Кориолиса. Случаи, когда ускорение Кориолиса равно нулю.

32. Сложное движение твёрдого тела. Сложение поступательных движений.

33. Сложение вращений тела вокруг осей (вращения направлены в одну сторону).

34. Сложение вращений вокруг параллельных осей (вращения направлены в разные сто­роны).

35. Сложение вращений вокруг пересекающихся осей.

36. Кинетические уравнения Эйлера.

37. Сложение поступательного и вращательного движений (векторы V_z и V_c направле­ны под любым углом друг к другу).

38. Методика расчета равновесия тела при сходящихся и произвольных силах.

39. Динамикам материальной точки. Основные законы динамики.

40. Две задачи динамики материальной точки. Несвободная материальная точка.

41. Динамика прямолинейного движения материальной точки.

42. Динамика криволинейного движения материальной точки.

43. Несвободное движение точки. Ур-ние движения точки п заданной неподвижной кривой.

44. Динамика относительного движения точки. Частные случаи.

45. Две меры механического движения. Кол-во движения и кинетическая энергия материальной точки. Импульс силы.

46. Теорема об изменении момента количества движения материальной точки.

47. Моменты количества движения точки относительно произвольного центра и оси.

48. Теорема об изменении момента количества движения материальной точки.

49. Работа силы. Мощность.

50. Примеры вычисления работы силы (работа сил тяжести, упругости пружины, трения).

51. Теорема об изменении кинетической энергии материальной точки.

52. Принцип Д'Аламбера для материальной точки.

53. Понятие механической системы (системы материальных точек). Внешние и внутренние силы.

54. Масса механической системы. Центр масс механической системы.

55. Моменты инерции твердых тел. Моменты инерции твердых тел относительно параллельных осей. Теорема Гюйгенса.

56. Моменты инерции твердых тел относительно параллельных осей. Теорема Гюйгенса.

57. Дифференциальные уравнения движения механической системы.

58. Теорема о движении центра масс механической системы. Закон сохранения движения центра масс.

59. Количество движения механической системы. Главный вектор количества движения.

60. Теорема об изменении количества движения механической системы. Закон сохранения количества движения механической системы.

61. Кинетический момент механической системы относительно центра и оси.

62. Кинетический момент абсолютно твердого тела относительно оси вращения.

63. Теорема об изменении кинетического момента механической системы. Закон сохранения кинетического момента механической системы.

64. Теорема о кинетической энергий механической системы в общем случае ее движения (Теорема Кенига).

65. Кинетическая энергия абсолютно твердых тел в различных случаях их движения.

66. Некоторые случаи вычисления работы сил. (Работа сил тяжести, работа сил, приложенных к вращающемуся телу, работа сил трения качения.

67. Теорема об изменении кинетической энергии механической системы.

68. Теорема об изменении кинетической энергии для неизменяемой механической системы и механической системы с идеальными связями.

69. Потенциальное силовое поле и силовая функция.

70. Потенциальная энергия механической системы. Закон сохранения механической энергии системы.

71. Принцип Д'Аламбера для механической системы.

72. Главный вектор и главный момент сил инерции механической системы (три случая движения).

73. Возможные перемещения механической системы. Число степеней свободы.

74. Принцип возможных перемещений.

75. Общее уравнение динамики (принцип Д'Аламбера-Лагранжа).

76. Голономные и неголономные связи. Обобщённые координаты, скорости и силы.

77. Дифф. ур-ния Лагранжа 2-го порядка.

1. Кинематика. Кинематика точки. Способы задания движения точки:

Кинематика – раздел мех-ки, в кот-ом изуч-ся дв-ие матер-ых тел в пространстве, причём в этом разделе не изуч-ся возд-ие сил, кот-ое опред-ет это дв-ие. В теор-ой мех-ке изуч-ся дв-ие точки, т.е. происходящее во вр-ни изм-ие положения тел относ-но друг друга. С одним из тел мы связываем систему отсчёта. Сущ-ет три способа для задания дв-ия точки: векторный, коор-ый и естественный. 1. Естественный. Дв-ие точки описывается в пространстве некоторой линией. Линия, представляющая собой геом-ое место послед-их положений точки с течением вр-ни в системе отсчёта наз-ся траекторией. Изуч-ие дв-ия точки состоит из опред-ия осн-ых характ-ик: 1. Начало отсчёта. 2. Положение точки в системе отсчёта. 3. Скорость точки. 4. Ускорение точки. 5. Закон дв-ия точки. По истечению вр-ни будет изм-ся дуговая коор-та, т.е. будут ф-ии вр-ни: S=БМ; S=f(t) (-ур-ие дв-ия при естественном способе задания её дв-ия). Если известен закон дв-ия точки, то задав начало отсчёта для каждого моменты вр-ни можно вычислить пройд-ый путь, дуговую коор-ту S, путём дифф-ия опред-ть ск-ть, напр-ие ск-ти и уск-ие.

2. Векторный. Положение точки опред-ся радиус-вектором r. Радиус-вектор с течением вр-ни не будет изм-ся. r=r(t) (-ур-ие дв-ия точки при векторном способе задания её дв-ия).

3. Коор-ый. Положение точки М опред-ся коор-ми x,y,z в декарт-ой системе коор-т. Каждая коор-та с течением вр-ни будет изм-ся. x=f₁(t); y=f₂(t); z=f₃(t) (-наз-ся ур-ем дв-ия точки в декарт-ых коор-тах).

2. Скорость точки. Вектор скорости:

3. Ускорение точки. Вектор ускорения:

4. Опред-ие ск-ти и уск-ия точки при коор-ом способе задания дв-ия:

Опред-ие ск-ти: Восп-ся ур-ем дв-ия точки при коор-ом способе задания, учитывая:

r(вектор)=i(вектор)*x+j(вектор)*y+k(вектор)*z (9)

V(вектор)=i(вектор)*dx/dt + j(вектор)*dy/dt + k(вектор)*dz/dt=dr(вектор)/dt (10)

V(вектор)=i(вектор)*Vx+j(вектор)*Vy+k(вектор)*Vz (11)

Сопоставим (10) и (11):

dVx=dx/dt; dVy=dy/dt; dVz=dz/dt (12)

Таким образом, зная закон дв-ия, ур-ие дв-ия точки при коор-ом способе задания, можно опред-ть путём дифф-ия проекции (параметр-ие ур-ия дв-ия точки). Можем вычислить проекции ск-тей на оси коор-т.

V=Sqr(Vx^2+Vy^2+Vz^2) (13)

Опред-м напр-ие ск-ти: cosa=Vx/V; cosb=Vy/V; cosj=Vz/V (14)

Опред-ие уск-ия: Восп-ся пред-щей методикой:

r(вектор)=i(вектор)*x+j(вектор)*y+k(вектор)*z

a(вектор)=d^2*r/dt^2 = i(вектор)*(d^2*x/dt^2)+ j(вектор)*(d^2*y/dt^2)+ k(вектор)*(d^2*z/dt^2) (17)

a(вектор)=i(вектор)*ax+j(вектор)*ay+k(вектор)*az (18)

Сопоставим (17) и (18). Запишем ax,ay,az:

ax=d^2*x/dt^2; ay=d^2*y/dt^2; az=d^2*z/dt^2 (19)

a=sqr(ax^2+ay^2+az^2) (20)

cosa=ax/a; cosb=ay/a; cosj=az/a (21)

5. Опред-ие ск-ти и уск-ия точки при естественном способе задания дв-ия:

Опред-ие ск-ти: Пусть известна траектория, напр-ие дв-ия, начало отсчёта и ур-ие дв-ия точки.

s=s(t) Восп-ся далее ф-лой (6): V(вектор)=dr(вектор)/dt (6)

Рассм-м r как ф-ию дуговой коор-ты S:

V(вектор)=dr(вектор)/dt=dr(вектор)/ds * ds/dt (где ds/dt – резул-т вычисления предела при t->0)

dr(вектор)/ds=ТАУ(вектор) (7) V(вектор)=ТАУ(вектор)*(ds/dt) (8) (- вычисл-ие ск-ти при естественном способе)

ds/dt – проекция ск-ти на касат-ую и наз-ся алгебраической величиной ск-ти.

Опред-ие уск-ия точки:

Вектор ускорения a точки лежит в соприкасающейся плоскости P  n и определяется двумя проекциями   и a_n (a_b = 0):

- проекция ускорения точки на касательную равна первой производной от алгебраической скорости или второй производной от криволинейной координаты точки по времени:  = d  / dt = d²s /dt² или   =   =   .

- проекция ускорения на главную нормаль равна квадрату скорости, деленному на радиус кривизны траектории в данной точке кривой: a_n = v² /   . Величины   и a_n соответственно называют  касательным и  нормальным ускорениями точки. Вектор ускорения a является векторной суммой касательной составляющей   , напраленной вдоль касательной P  , и нормальной составляющей a_n, направленной вдоль главной нормали Pn: a =   + a_n. При этом составляющая   может быть направлена или в положительном, или в отрицательном направлении оси P  в зависимости от знака проекции   , а составляющая a_n будет всегда направлена в сторону вогнутости кривой, так как проекция a_n   0. Так как эти составляющие взаимно перпендикулярны, то модуль вектора a определяется по формуле: a = (  ² + a_n² )  . Рассмотрим теперь геометрическую характеристику траектории точки, называемую радиусом кривизны   . Радиус кривизны кривой в какой-либо ее точке равен радиусу окружности, которая наилучшим образом аппроксимирует по сравнению с другими окружностями участок кривой из малой окрестности рассматриваемой точки. Величина, обратная радиусу кривизны, называется кривизной кривой k = 1 /   в данной точке. В частности, для окружности радиус кривизны одинаков во всех ее точках и равен ее радиусу:   = R (кривизна окружности k = 1 / R); для прямой радиус кривизны   =   (кривизна прямой k = 0).

Рассмотрим условия, при которых касательное и нормальное ускорения обращаются в нуль.

- Касательное ускорение равно нулю, если   = d  / dt = 0.  Это условие выполняется, если все время v = |   | = const, то есть при равномерном движении точки по траектории любой формы.  Касательное ускорение обращается в нуль также в те моменты времени, в которые алгебраическая скорость   достигает экстремума, например максимума или минимума.

- Нормальное ускорение равно нулю, если a_n = v² /   = 0.  Это условие выполняется, если   =   , то есть при прямолинейном движении точки. При движении точки по криволинейной траектории   =   в точках перегиба, в которых происходит изменение выпуклости траектории на вогнутость, и наоборот.  Нормальное ускорение обращается в нуль также в моменты времени, в которые v = 0, то есть в моменты изменения направления движения точки по траектории. 

Общие формулы для вычисления касательного и нормального ускорений, а также условия обращения их в нуль, показывают, что

- касательное ускорение характеризует изменение вектора скорости по величине;

- нормальное ускорение характеризует изменение вектора скорости по направлению.

6. Годограф ск-ти. Касат-ое, норм-ое и полное уск-ие. Естественный треуг-к. Радиус кривизны:

Годограф ск-ти V(вектор). Изобразим траекторию и укажем ск-ть в выбранные моменты вр-ни.

Выберем точку 0 и путём парал-ого переноса построим V1, V2, V3… Проведём линию через концы этих векторов ск-ти, наз-ём эту линию годографом ск-ти. Годограф ск-ти представляет собой геом-ое место концов векторов ск-тей движ-ся точки, построенной из одной и той же, произвольно выбранной точки 0. Годограф ск-ти опред-ет напр-ие уск-ия в заданный момент вр-ни, как вектор напр-ый по касат-ой к годографу ск-ти.

Радиусом кривизны кривой   в точке   называется число  , где   - кривизна линии   в точке  . Если кривизна в точке   равна 0, то радиус кривизны формально полагаем равным  .     

Заметим, что для окружности это определение даёт значение радиуса кривизны, совпадающее с радиусом окружности (постоянное во всех точках окружности). Без доказательства сообщим, что из всех окружностей, касающихся линии   в фиксированной точке  , наиболее плотно прилегает

к линии   та окружность, которая имеет радиус, равный радиусу кривизны кривой в точке  , и выпуклость в ту же сторону, что кривая  . Эта окружность называется окружностью кривизны линии   в точке  . 

Касат-ое и норм-ое уск-ия:

7. Кинематика тв-ого тела. Виды дв-ия тв-ого тела. Поступ-ое дв-ие тв-ого тела:

Абсолютно твердым телом называется материальное тело, геометрическая форма которого и размеры не изменяются ни при каких механических воздействиях со стороны других тел, а расстояние между любыми двумя его точками остается постоянным. Существует пять видов движения твердого тела:

1) поступательное движение;

2) вращение вокруг неподвижной оси;

3) плоское движение;

4) вращение вокруг неподвижной точки;

5) свободное движение.

Первые два называются простейшими движениями твердого тела.

Поступательным называется такое движение твердого тела, при котором любая прямая, проведенная в этом теле, перемещается, оставаясь параллельной своему начальному направлению. Поступательное движение не следует смешивать с прямолиней­ным. При поступательном движении тела траектории его точек мо­гут быть любыми кривыми линиями.

8. Вращ-ое дв-ие тв-ого тела. Угловая ск-ть и угл-ое уск-ие:

Вращательным движением твердого тела вокруг неподвижной оси называется такое его движение, при котором какие-нибудь две точки, принадлежащие телу (или неизменно с ним связанные), остаются во все время движения неподвижными (рис.13). Проходящая через неподвижные точки А и В прямая АВ называется осью вращения. Так как расстояния между точками твердого тела должны оста­ваться неизменными, то очевидно, что при вращательном движении все точки, принадлежащие оси вращения, будут неподвижны, а все остальные точки тела будут описывать окружности, плоскости которых перпендикулярны оси вращения, а центры лежат на этой оси. Для определения положения вращаю­щегося тела проведем через ось вращения, вдоль которой направим ось  , полуплос­кость  - неподвижную и полуплоскость, врезанную в само тело и  вращающую­ся вместе с ним (рис. 13).

рис 13

Тогда поло­жение тела в любой момент времени одно­значно определится взятым с соответствую­щим знаком углом   между этими полуплоскостями, который назо­вем углом поворота тела. Будем считать угол   положительным, если он отложен от неподвижной плоскости в направлении против хода часовой стрелки (для наблюдателя, смотрящего с положительного конца оси  ), и отрицательным, если по ходу часовой стрелки. Измерять угол    будем всегда в радианах. Чтобы знать положение тела в любой момент времени, надо знать зависимость угла   от времени t, т.е. . Уравнение  выражает закон вращательного движения твердого тела вокруг неподвижной оси. Основными кинематическими характеристиками вращательного движения твердого тела являются его угловая скорость   и угловое ускорение  . Если за промежуток времени   тело совершает поворот на угол  , то численно средней угловой скоростью тела за этот промежуток времени будет  . В пределе при   найдем, что 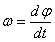 или  . Таким образом, числовое значение угловой скорости тела в данный момент времени равно первой производной от угла поворота по времени. Знак   определяет направление вращения тела. Легко видеть, что когда вращение происходит против хода часовой стрелки,  >0, а когда по ходу часовой стрелки, то  <0. Размерность угловой скорости 1/Т (т.е. 1/время); в качестве единицы измерения обычно применяют рад/с или, что тоже, 1/с (с^-1), так как радиан - величина безразмер­ная. Угловое ускорение характеризует изменение с те­чением времени угловой скорости тела. Если за промежуток вре­мени   угловая скорость тела изменяется на величину  , то числовое значение среднего углового ускорения тела за этот промежуток времени будет . В пределе при   найдем,   или   . Таким образом, числовое значение углового ускорения, тела в данный момент времени равно первой производной от угловой скорости или второй производной от угла поворота тела по времени. Размерность углового ускорения 1/T² (1/время²); в качестве единицы измерения обычно применяется рад/с² или, что то же, 1/с²  (с-²). Если модуль угловой скорости со временем возрастает, вращение тела называется ускоренным, а если убывает, - замедленным. Легко видеть, что вращение будет ускоренным, когда величины   и   имеют одинаковые знаки, и замедленным, - когда разные. Угловое ускорение тела (по аналогии с угловой скоростью) можно также изобразить в виде вектора  , направленного вдоль оси вращения. При этом . Направление   совпадает с направлением  , когда тело вращается ускоренно и противоположно   при замедленном вращении.