45. Плоские зубчатые механизмы
Плоский зубчатый механизм – это механизм, в котором зубчатые колеса совершают движения в одной плоскости.
К механизмам данного вида относятся:
цевочные (рис. 6.3);
цилиндрические (рис. 6.5);
торцевые (рис. 6.6, а);
реечные (рис. 6.6, б).
Цевочный механизм – это механизм с параллельными геометрическими
осями вращения звеньев, одно из которых имеет специальные цилиндриче-
ские выступы-цевки (рис. 6.3).
Структурный анализ. Цевочные механизмы являются представителями
плоских механизмов, следовательно, определение подвижности проводится
по формуле Чебышева, представленной в степенях подвижностей кинемати-
ческих пар. Структура цевочных механизмов содержит: стойку 0, звездочку 1
и цевочное колесо 2. При этом звездочка 1 и цевочное колесо 2 являются
подвижными звеньями, следовательно, n = 2. Подвижные звенья, взаимодей-
ствуя со стойкой, образуют две вращательные кинематические пары с под-
вижностью, равной единице: 0 − 1, 2 − 0, а контакт подвижных звеньев друг с
другом свидетельствует о существовании высшей кинематической пары с
подвижностью, равной двум: 1 − 2, следовательно, , p1 = 2, 2 p =1.
Подставив полученные данные в структурную формулу, получим
W =3⋅2−2⋅2−1=6−4−1=1.
Результат означает, что для однозначного определения взаимного рас-
положения звеньев механизмов данного вида достаточно одной обобщенной
координаты.
В цевочных механизмах преобразование движения и силовых факторов
осуществляется путем непосредственного касания рабочей поверхности звез-
дочки 1 с рабочими поверхностями цевок цевочного колеса не изменяет подвижность цевочного механизма и не влияет на его передаточные функции, а является местной подвижностью.
Цилиндрический зубчатый механизм – это зубчатый механизм с параллельными геометрическими осями колес, которые имеют начальные цилиндрические поверхности.
Для простых цилиндрических зубчатых механизмов характерно наличие двух видов зацепления: внешнего и внутреннего.
Внешнее зацепление − это вид зацепления цилиндрических зубчатых
колес, в котором геометрические центры этих колес лежат по разные стороны относительно нормали n − n к линии центров прямой 1 2 OO , проведенной
через полюс зацепления (рис. 6.4).
Внутреннее зацепление − это вид зацепления цилиндрических зубчатых
колес, в котором геометрические центры этих колес лежат по одну сторону
относительно нормали n − n к линии центров прямой 1 2 OO , проведенной че-
рез полюс зацепления (рис. 6.5).
Структурный анализ. Цилиндрические зубчатые механизмы являются
представителями плоских механизмов, следовательно, определение подвижности проводится по формуле Чебышева, представленной в степенях подвижностей кинематических пар.
Независимо от вида зацепления, цилиндрические зубчатые механизмы
(рис. 6.3, рис. 6.4) образованы двумя подвижными звеньями 1 и 2, следовательно,
n = 2. Подвижные звенья и стойка образуют две вращательные кинематические пары с подвижностью, равной единице: 0 − 1, 2 − 0, и одну высшую кинематическую пару с подвижностью, равной двум: 1 − 2, следовательно, , p1 = 2, 2 p =1.
Подставив полученные данные в структурную формулу, имеем
W =3⋅2−2⋅2−1=6−4−1=1.
Результат означает, что для однозначного определения взаимного рас-
положения звеньев механизмов данного вида достаточно одной обобщенной
координаты.
Кинематический анализ. Для решения задач кинематического анализа
воспользуемся характерными точками механизма, в качестве которых выбираем геометрические центры кинематических пар. Скорости остальных точек определим, используя свойства годографов скоростей. Под годографом скоростей
точек звена механизма понимается прямая, проходящая через вершину вектора
скорости характерной точки и мгновенный центр скоростей данного звена.
Скорость точки А, принадлежащей колесу 1 простого зубчатого меха-
низма (рис. 6.4, рис. 6.5),
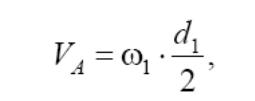
где d1 − делительный диаметр колеса 1.
Скорость точки А, принадлежащей колесу 2 простого зубчатого меха-
низма,
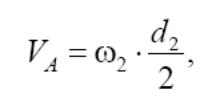
где d2 − делительный диаметр колеса 2.
Независимо от вида зацепления, контакт зубчатых колес происходит в
полюсе зацепления,а из основной теоремы зацепления следует равенство
скоростей точек сопряженных профилей:
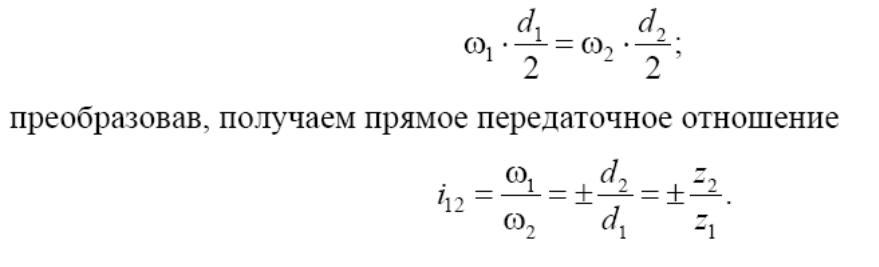
Знак «−» означает, что входное и выходное звенья цилиндрического
зубчатого механизма с внешним зацеплением вращаются в разных направле-
ниях, т. е. происходит смена направления вращения на выходном звене по
сравнению с направлением вращения на входном звене (рис. 6.4). Знак «+» в
выражении говорит, что входное и выходное звенья цилиндрического зубча-
того механизма с внутренним зацеплением вращаются в одном направлении,
т. е. смены направления вращения на выходном звене, по сравнению с на-
правлением вращения на входном звене, не происходит (рис. 6.5).
Повышение нагрузочной способности при сохранении габаритов обес-
печивается формированием цилиндрических зубчатых механизмов с зубча-
тыми колесами, имеющими косую (рис. 6.6, б) или криволинейную линию
зубьев (рис. 6.6, в). Данные виды цилиндрических зубчатых механизмов ра-
ботают при средних (от 3 до 15 м/с) или больших (выше 15 м/с) окружных
скоростях и имеют существенных недостаток: появление в процессе работы
дополнительных осевых усилий. Исключить данный недостаток позволяют
шевронные цилиндрические зубчатые механизмы (рис. 6.6, г), которые обла-
дают более высокой нагрузочной способностью, что является следствием
увеличения площади контакта зубьев колес.
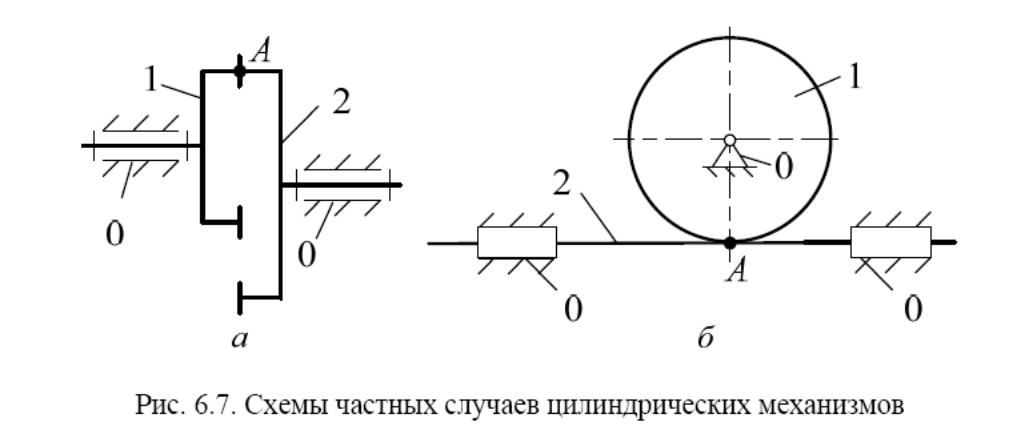
Одной из разновидностей цилиндрических механизмов являются меха-
низмы с торцевым зацеплением, или торцевые механизмы (рис. 6.7, а).
Структура подобных механизмов содержит стойку и два зубчатых колеса с
торцевыми зубьями, имеющие выпуклые рабочие поверхности. Цилиндриче-
ские механизмы с торцевым зацеплением сочетают основные достоинства
цилиндрических и конических механизмов.
Частным случаем цилиндрических механизмов являются реечные ме-
ханизмы (рис. 6.7, б). Структура реечных механизмов содержит стойку и два
колеса, одно из которых имеет рабочую поверхность в виде развертки на-
чальной цилиндрической окружности и называется рейка 2. Механизмы по-
добного вида являются реверсивными и могут работать как в режиме редук-
тора, так и в режиме мультипликатора, следовательно, обладают двумя вида-
ми передаточного отношения.
Прямое передаточное отношение
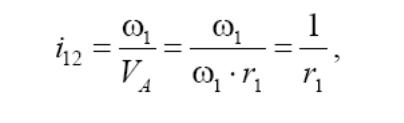
где VА − линейная скорость точки контакта звеньев механизма; 1 r − радиус
делительной окружности зубчатого колеса 1.
Обратное передаточное отношение
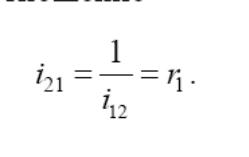
Реечные механизмы применяются для преобразования вращательного
движения колеса 1 в поступательное движение рейки 2 или наоборот.