39. Метод Виттенбеуэра. Диаграмма «энергия-масса». Назначение диаграммы.

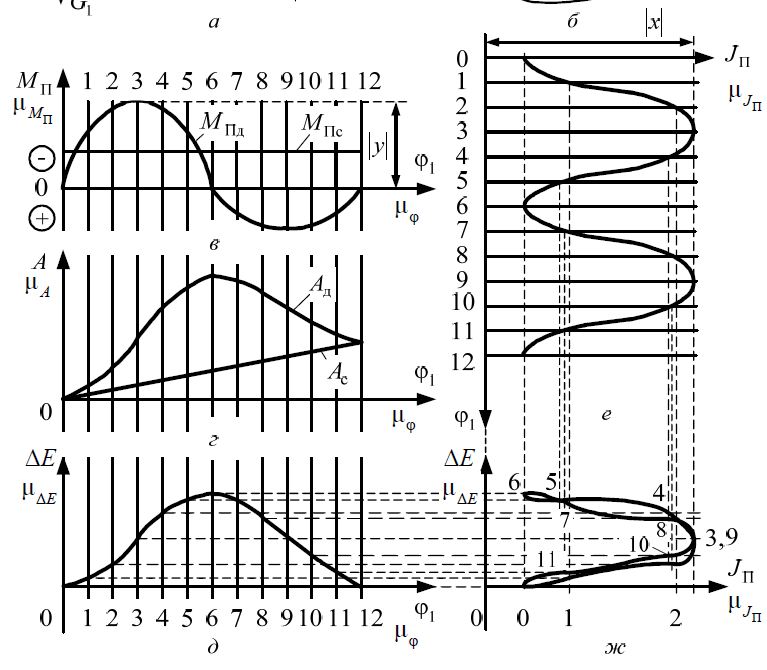
Для определения момента инерции маховой массы к диаграмме «энер-

гия−масса» до пересечения с осью ΔЕ проводятся касательные. Углы наклона

касательных соответствуют максимальному и минимальному значениям уг-

ловой скорости ведущего звена механизма

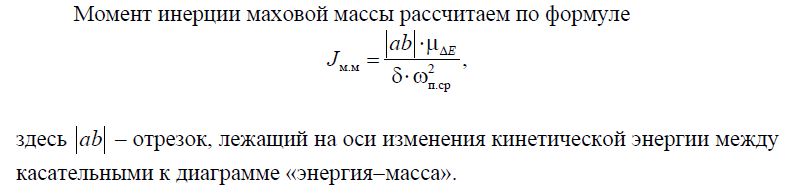
Назначение диаграммы – определение момента инерции маховой массы, чтобы можно было ввести в систему дополнительный момент инерции маховой массы, для реализации более равномерного хода механизма.

40.Механизмы с высшей кп. Классификация механизмов с высшей кп. Примеры.

Механизм с высшей кинематической парой − это механизм, структура

которого содержит хотя бы одну высшую кинематическую пару.

К типовым механизмам данного вида относятся:

механизмы фрикционные (рис. 5.4, рис.5.5);

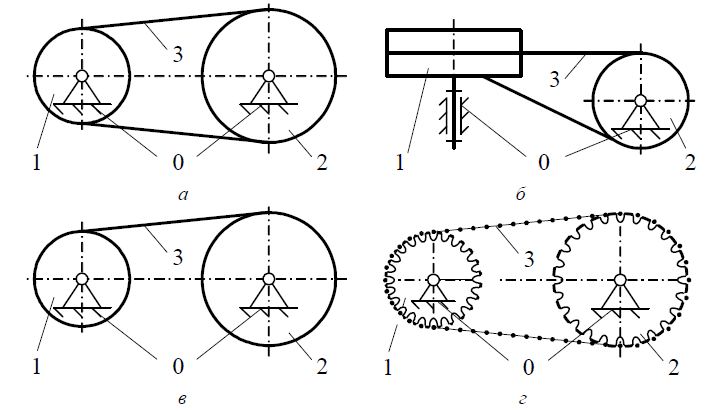
механизмы с гибкими звеньями (рис. 5.6, рис.5.7);

механизмы мальтийские (рис. 5.8, а);

механизмы поводковые (рис. 5.8, б);

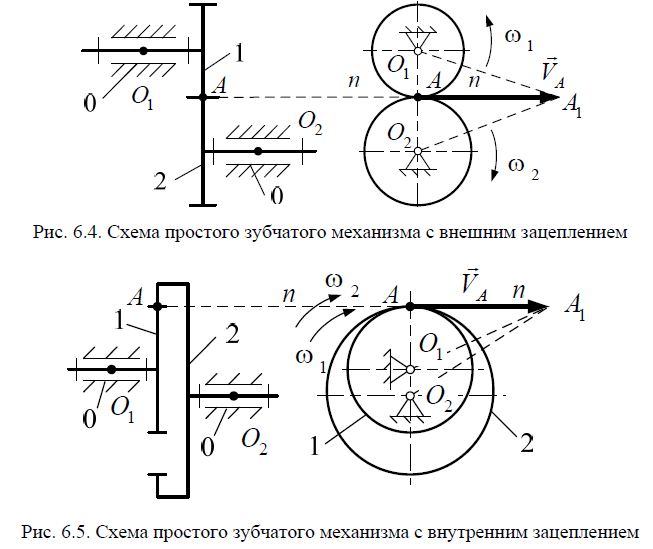
механизмы зубчатые (рис. 6.1, рис.6.4, рис.6.5, рис.6.6);

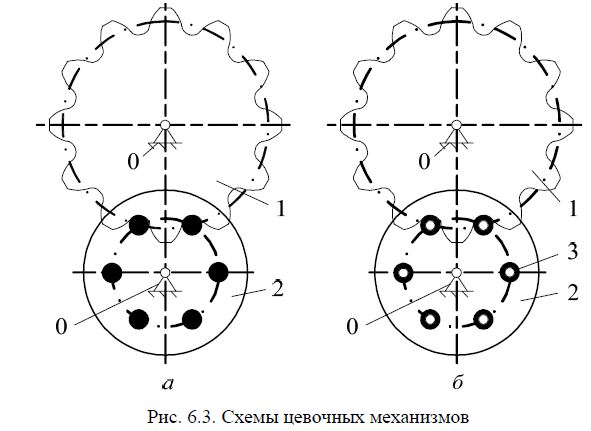
механизмы цевочные (рис. 6.3.);

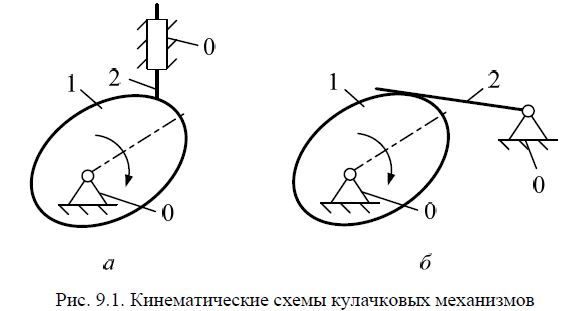
механизмы кулачковые (рис. 9.1).

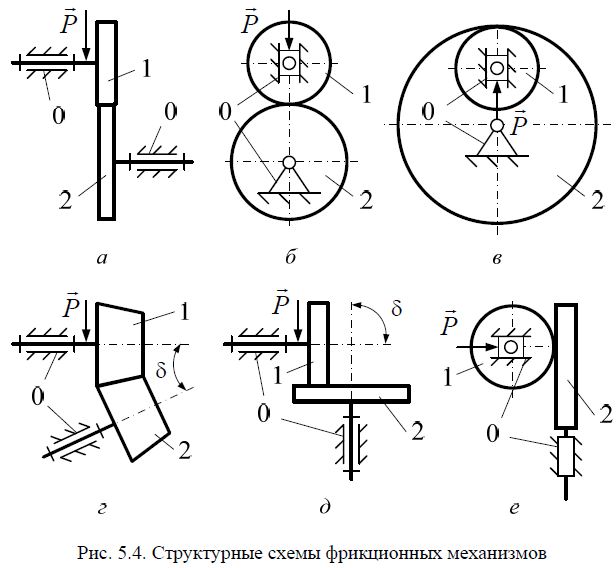
Фрикционный механизм − это механизм с высшей кинематической па-

рой, в котором передача движения и преобразование силовых факторов осу-

ществляется за счет сил трения или сцепления.

В механизмах с гибкими звеньями преобразование движения и силовых

факторов осуществляется посредствам изменения формы рабочих поверхно-

стей гибкого звена.

Мальтийский механизм – это механизм, содержащий кривошип,

имеющий специальный выступ-палец прерывисто сцепляющийся с пазом

выходного звена.

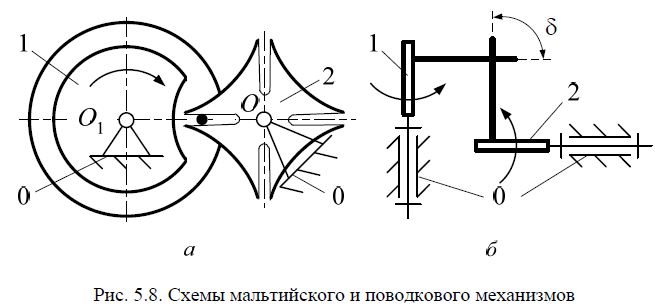
Поводковый механизм – это механизм, подвижные звенья которого

имеют специальные цилиндрические выступы-пальцы.

Зубчатый механизм – это механизм с высшей кинематической парой, в

структуру которого входят звенья, снабженные специальными выступами-

зубьями.

Цевочный механизм – это механизм с параллельными геометрическими

осями вращения звеньев, одно из которых имеет специальные цилиндриче-

ские выступы-цевки.

Кулачковый механизм − это механизм с высшей кинематической парой,

обладающий возможностью обеспечения выстоев выходного звена, а структура

содержит хотя бы одно звено с рабочей поверхностью переменной кривизны.

41.Теорема о высшей кинематической паре

Поверхности звеньев, образующих высшую кинематическую пару и

обеспечивающие заданные законы их относительного движения, называются

сопряженными, или начальными.

На относительное движение начальных поверхностей звеньев наклады-

вается ограничение, которое называется теоремой о высшей кинематической

паре: в каждой точке касания начальных поверхностей, вектор скорости VP

этой точки лежит на перпендикуляре к общей нормали n−n, проведенной че-

рез точку касания (рис. 5.1).

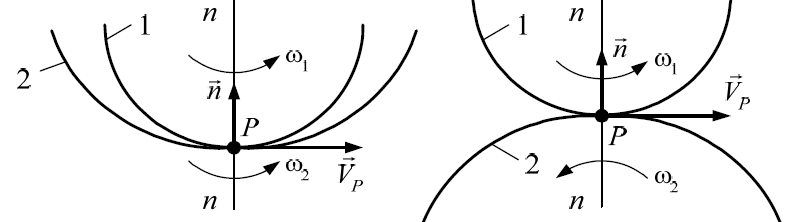
Рис. 5.1. Вектор скорости точки контакта сопряженных поверхностей

Условие основной теоремы высшей пары:

в векторном виде

VP ⋅n= 0

в аналитическом виде

VP⋅n⋅cos(VP, n)=0

где n– единичный вектор, направленный по общей нормали n−n.

Теорема доказывается «от противного». Если условие теоремы не вы-

полняется, т. е. вектор скорости точки контакта начальных поверхностей не

лежит на перпендикуляре к общей нормали, тогда имеется составляющая

этой скорости, направленная по общей нормали. В этом случае происходит

либо отрыв одной поверхности от другой, либо внедрение этих поверхностей

друг в друга, что недопустимо для существования кинематической пары как

подвижного соединения. Следовательно, составляющая скорости точки кон-

такта начальных поверхностей не действует по общей нормали, а это воз-

можно только при условии, что вектор скорости этой точки лежит на перпен-

дикуляре к общей нормали, т. е. условие теоремы выполняется. Теорема до-

казана.

ОСНОВНАЯ ТЕОРЕМА СОПРЯЖЕНИЯ (ЗАЦЕПЛЕНИЯ)

В плоских механизмах с высшими кинематическими парами вместо со-

пряженных или начальных поверхностей рассматривают сопряженные или

начальные профили (окружности).

Сопряженные или начальные профили − это кривые, получаемые в се-

чении сопряженных или начальных поверхностей плоскостью, проведенной

параллельно плоскости их движения.

Пусть звенья 1 и 2 плоского механизма с высшей кинематической парой

совершают вращательные движения вокруг параллельных осей в разных направ-

лениях (рис. 5.3). При этом точка А принадлежит звену 1, а точка В – звену 2.

Значения скоростей точек А и В выражаются:

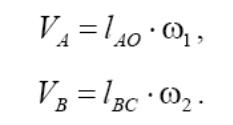
Звенья 1 и 2 образуют высшую кинематическую пару, следовательно,

контакт начальных профилей рассматриваемых звеньев имеет место в полюсе сопряжения P. Полюс сопряжения P является мгновенным центром скоро-

стей в относительном движении звеньев.

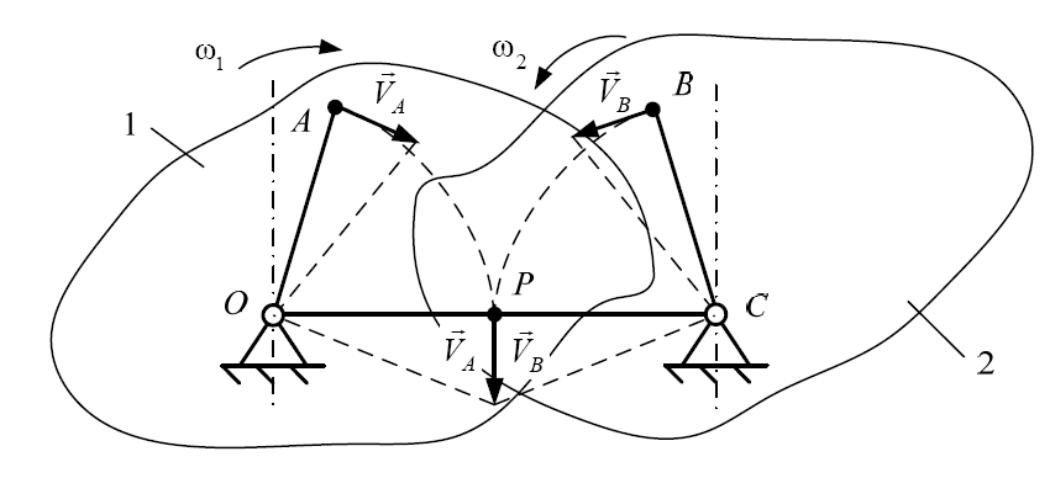рис 5.3

Из теоремы о высшей кинематической паре следует: вектора скоростей

точек контакта начальных профилей, расположенные в полюсе сопряжения,

действуют по прямой, являющейся перпендикуляром к общей нормали. Об-

щая нормаль начальных поверхностей совпадает с прямой ОС, следователь-

но, полюс P должен лежать на перпендикуляре к этой прямой. Кроме того,

мгновенный центр P должен лежать на прямой ОС, т. к. только в точках этой

прямой вектора скоростей точек А и В имеют одинаковое направление. В по-

люсе сопряжения скорость относительного движения звеньев 1 и 2 равна ну-

лю, а скорости точек А и В равны друг другу:

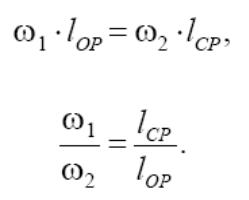
Из проведенного анализа следует: общая нормаль в точке касания на-

чальных профилей проходит через полюс сопряжения P, который делит ме-

жосевое расстояние ОС на части, отношение значений которых обратно про-

порционально отношению угловых скоростей звеньев.

В теории зубчатых механизмов сделанный вывод носит название ос-

новной теоремы зацепления, которая доказана Виллисом. Основная теорема

зацепления рассматривает отношение угловых скоростей звеньев, которое

называется кинематическим передаточным отношением:

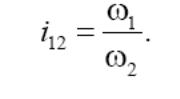
Полученное выражение определяет основное свойство теоремы зацеп-

ления, которая имеет следующую формулировку: передаточное отношение

звеньев, совершающих вращательные движения, прямо пропорционально от-

ношению угловых скоростей и обратно пропорционально отношению рас-

стояний от центров вращения до полюса.

42. ЗУБЧАТЫЕ МЕХАНИЗМЫ

Зубчатый механизм – это механизм с высшей кинематической парой, в

структуру которого входят звенья, снабженные специальными выступами-

зубьями.

Зубчатые механизмы обладают рядом полезных свойств, обусловивших

их широкое распространение практически во всех видах машин.

Однако наибольшее распространение зубчатые механизмы получили в каче-

стве передаточных или преобразующих устройств, используемых в более

сложных технических системах для согласования характеристик рабочей и

энергетической машин.

Зубчатые механизмы предназначены для передачи вращательного

движения между звеньями, а также для изменения значений угловой ско-

рости и силовых факторов. Зубчатые механизмы, предназначенные для

уменьшения угловой скорости выходного звена с одновременным повы-

шением крутящего момента по сравнению с входными значениями этих

параметров, называются редукторами, а зубчатые механизмы, предназна-

ченные для увеличения угловой скорости с потерей значения крутящего

момента на выходном звене, – мультипликаторами.

Типовой зубчатый механизм состоит из стойки и двух подвижных

звеньев, которые называются зубчатыми колесами.

Зубчатое колесо − это звено зубчатого механизма, снабженное специ-

альными выступами-зубьями.

В зависимости от особенностей структуры, все зубчатые механизмы

подразделяются на два вида: простые и сложные.