57. Эпициклические зубчатые механизмы. Типовые планетарные механизмы. Звенья планетарных механизмов. Особенности структуры. Пример выполнения структурного механизма.
Однорядные, многорядные и многопоточные зубчатые механизмы являются представителями сложных зубчатых механизмов с неподвижными
осями вращения зубчатых колес. С помощью механизмов перечисленных
видов не всегда удается обеспечить выполнение заданных условий. В этом
случае применяются сложные зубчатые механизмы с подвижными геометрическими осями вращения колес. Подобные механизмы называются эпициклическими.
Эпициклический зубчатый механизм – это сложный зубчатый механизм, имеющий в своей структуре хотя бы одно звено с подвижной геометрической осью вращения.
К эпициклическим зубчатым механизмам относятся: планетарные
(рис. 7.4) и дифференциальные механизмы (рис. 7.9, а).
Планетарный зубчатый механизм – это эпициклический зубчатый механизм с подвижностью, равной единице.
К типовым планетарным механизмам относятся:
однорядный планетарный зубчатый механизм с одним внешним и од-
ним внутренним зацеплением (рис. 7.4, а);
двухрядный планетарный зубчатый механизм с одним внешним и од-
ним внутренним зацеплением (рис. 7.4, б);
двухрядный планетарный зубчатый механизм с двумя внешними зацеплениями (рис. 7.4, в);
двухрядный планетарный зубчатый механизм с двумя внутренними зацеплением (рис. 7.4, г).
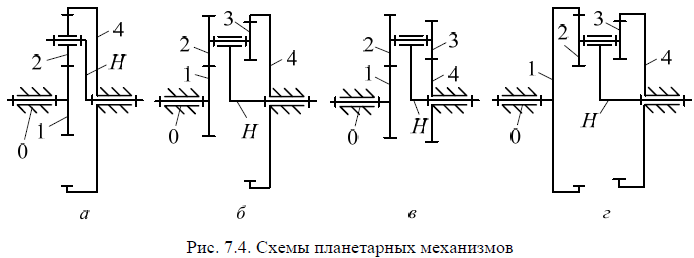
Независимо от схемы (рис. 7.4), структура планетарных зубчатых механизмов содержит следующие звенья: солнечное колесо, корона, один или
нескольких сателлитов и водило.
Солнечное колесо – это зубчатое колесо с внешними зубьями, расположенное в центре планетарного механизма.
Корона – это зубчатое колесо планетарного механизма с внутренними
зубьями.
Сателлит – это зубчатое колесо планетарного механизма, геометрическая ось вращения которого является подвижной.
Водило – это подвижное звено планетарного механизма, на котором установлены сателлиты.
Солнечное колесо в схемах планетарных механизмов (рис. 7.4, а−в) представлено подвижным звеном 1, а в схеме (рис. 7.4, г) солнечное колесо отсутствует. При этом схема планетарного механизма (рис. 7.4, в) помимо подвижного солнечного колеса 1 содержит и неподвижное солнечное колесо 4. Короной в
схемах планетарных механизмов (рис. 7.4, а, б, г) является неподвижное
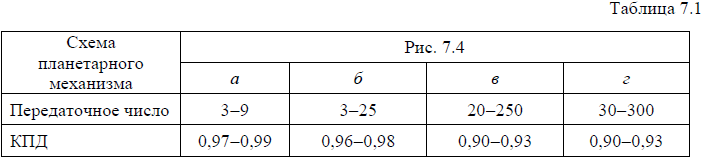
колесо 4, а в схеме (рис. 7.4, в) корона отсутствует. При этом схема планетарного механизма (рис. 7.4, г) помимо неподвижной короны 4 содержит и подвижную корону 1. Сателлитом в планетарных механизмах является подвижное колесо 2. В схеме (рис. 7.4, а) сателлит представлен одним колесом, а в схемах (рис. 7.4, б−г) сателлит – это блок зубчатых колес 2 и 3. Водило во всех схемах планетарных механизмов представлено в виде рычажной системы H и предназначено для установки сателлитов и обеспечения вращательного движения этих звеньев как вокруг собственной оси вращения, так и вокруг оси вращения водила Н. В зависимости от схемы планетарного механизма возможная реализация сочетаний значений КПД и величин передаточных чисел представлена
в табл. 7.1.
Структурный анализ. Все схемы планетарных механизмов (рис. 7.4) образованы последовательным соединением простых зубчатых механизмов, которые являются плоскими механизмами. Следовательно, для определения
подвижности данного механизма можно воспользоваться формулой Чебышева. Из анализа схем планетарных механизмов (рис. 7.4) вытекает: все планетарные механизмы состоят из стойки 0, трех подвижных звеньев 1, 2 и Н. Корона 4 является неподвижным звеном, следовательно, является элементом стойки 0. В этом случае n = 3 .
Все схемы планетарных механизмов (рис. 7.4) содержат по три одноподвижные кинематические пары: 0 – 1, 2 – H, H – 0 и по две высшие кинематические пары: 1 – 2, 2 – 0 с подвижностью, равной двум, тогда p1 = 3, а p2 = 2.
Подставив значения коэффициентов в формулу Чебышева, получим
W = 3⋅3 − 2 ⋅3 − 2 =1.
Результат означает, что для однозначного определения взаимного рас-
положения звеньев любой схемы типового планетарного механизма (рис. 7.4)
достаточно одной обобщенной координаты.