52. Показатели качества зубчатых механизмов.

 К качественным показателям цилиндрического эвольвентного прямозубого механизма относятся:

коэффициент полезного действия η;

коэффициент перекрытия εα;

коэффициент удельного скольжения λ;

коэффициент формы зуба Y;

коэффициент удельного давления ϑ.

Коэффициент полезного действия − это величина, характеризующая

количество полезно используемой механизмом суммарной энергии.

КПД механизма определяется по выражению

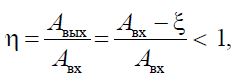
53. Классификация сложных зубчатых механизмов. Примеры.

Сложный зубчатый механизм − это зубчатый механизм, образованный

числом зубчатых колес больше двух.

Сложные зубчатые механизмы подразделяются:

1) по количеству рядов:

однорядные механизмы (рис. 7.1, а);

многорядные механизмы (рис. 7.2, а);

2) по числу потоков механической энергии:

однопоточные механизмы (рис. 7.1, а, рис.7.2, а);

многопоточные механизмы (рис. 7.3, а);

3) по кинематическому состоянию осей вращения зубчатых колес:

механизмы с неподвижными осями вращения колес (рис. 7.1, а, рис.7.2,

а, рис. 7.3, а);

механизмы с подвижными осями вращения колес (рис. 7.4);

4) по количеству входных и выходных звеньев:

механизмы с одним входным и одним выходным звеном (рис. 7.1, а,

рис. 7.2, а, рис. 7.3, а, рис. 7.4);

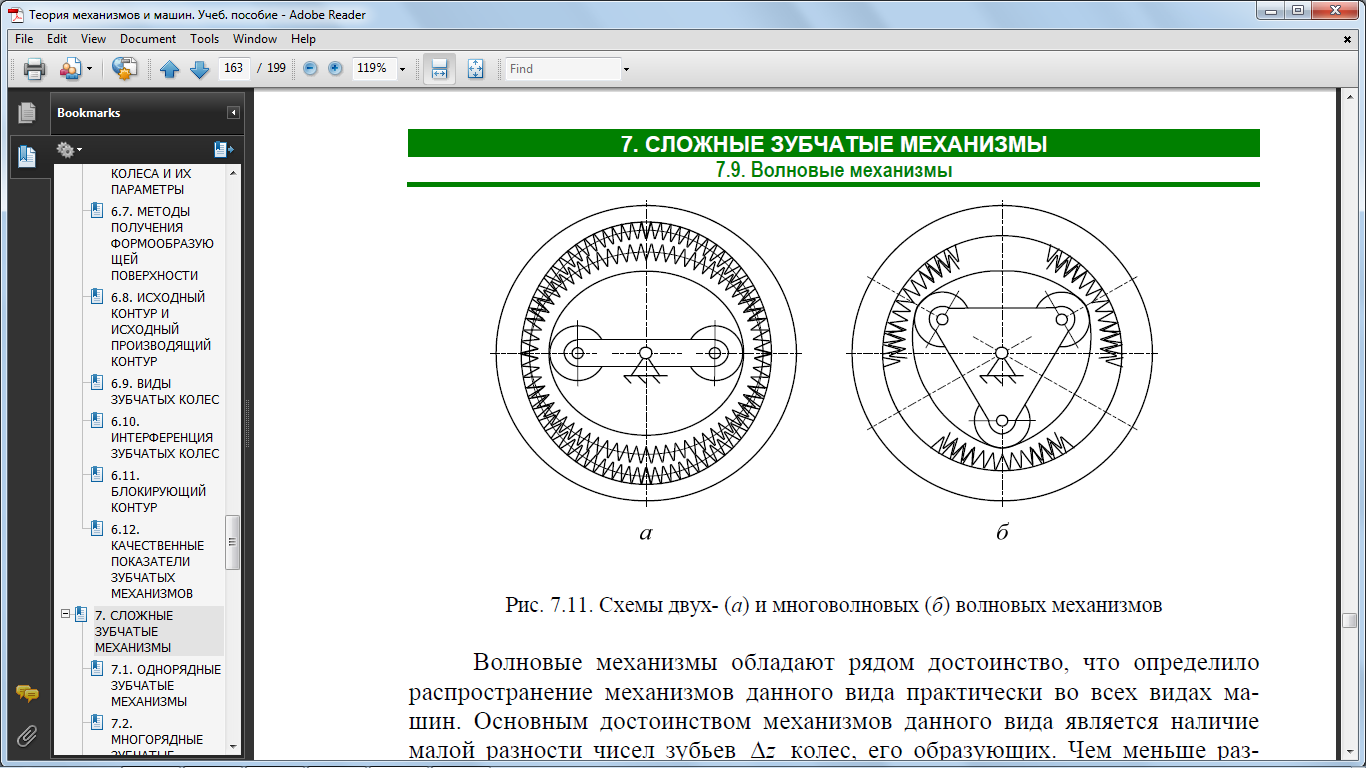
механизмы с одним входным и несколькими выходными звеньями

(рис. 7.9, а);

механизмы с несколькими входными и одним выходным звеном

(рис. 7.9, а);

механизмы с несколькими входными и выходными звеньями;

5) по виду передаточной функции:

механизмы с постоянной передаточной функцией (рис. 7.1, а,

рис. 7.2, а, рис. 7.3, а);

механизмы с переменной передаточной функцией (рис. 7.9);

6) по виду звеньев:

механизмы с жесткими звеньями (рис. 7.1, а, рис. 7.2, а, рис. 7.3, а,

рис. 7.4);

механизмы с деформируемыми звеньями (рис. 7.10, рис. 7.11).

Рассмотрим разновидности сложных зубчатых механизмов, состоящих

из цилиндрических механизмов.

54. Однорядные зубчатые передачи. Структурный и кинематический анализ.

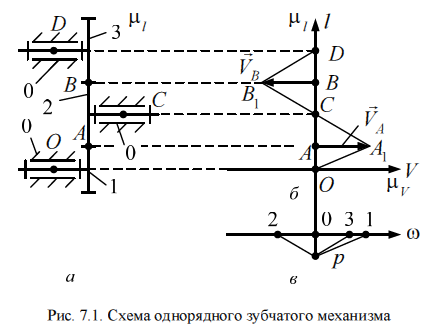
Однорядный зубчатый механизм-это сложный зубчатый механизм,

Образованный последовательным соединением простых зубчатых механизмов с расположением всех зубчатых колес в один ряд(рис. 7.1, а).

7. СЛОЖНЫЕ ЗУБЧАТЫЕ МЕХАНИЗМЫ

Структурный анализ. Схема сложного однорядного зубчатого механизма(рис. 7.1, а) образована последовательным соединением простых зуб-

чатых цилиндрических механизмов, относящихся к плоским механизмам,

следовательно, рассматриваемый механизм также является плоским, подвижность которого определяется по формуле Чебышева.

Из анализа схемы механизма вытекает: сложный однорядный зубчатый

Механизм состоит из стойки 0, представленной тремя шарнирно-неподвижными

Опорами и трех подвижных звеньев1, 2, 3, т. е. n = 3.

Стойка0 с подвижными звеньями 1, 2, 3 создает три одноподвижные

Кинематические пары: 0 - 1, 2 - 0, 3 - 0, а зубчатыеколеса1, 2, 4 между собой образуют две высшие кинематические пары: 1 - 2, 2 - 3 с подвижностью

Равной двум, тогда р1 = 3, ар2 = 2.

Подставив значения коэффициентов в формулу Чебышева, получим

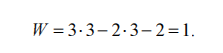
Результат означает, что для однозначного определения взаимного рас-

Положения звеньев сложного однорядного зубчатого механизма(рис. 7.1, а)

Достаточно одной обобщенной координаты.

Кинематический анализ. Сложный однорядный зубчатый механизм

(рис. 7.1, а) образован последовательным соединением простых зубчатых механизмов, следовательно, передаточное отношение данного механизма раскладывается на передаточные отношения простых механизмов:

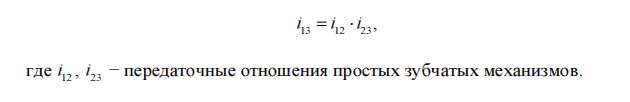
Полученное равенство представляет собой прямое передаточное отношение сложного однорядного зубчатого механизма от шестерни 1 (ведущего

колеса) к выходному колесу 3. Знак «+» означает, что шестерня 1 и выходное

звено 3 вращаются в одном направлении. Анализ выражения показывает, что

передаточное отношение сложного однорядного зубчатого механизма не за-

висит от параметров колеса 2, являющегося паразитным зубчатым колесом.

Паразитное зубчатое колесо − это зубчатое колесо, геометрические

параметры которого не оказывают влияния на передаточные отношения

сложного механизма.

Паразитные зубчатые колеса вводится в структуру сложных зубчатых

механизмов с целью изменения направления вращения выходного звена.

Сложные однорядные зубчатые механизмы являются реверсивными,

могут работать в режиме редуктора или мультипликатора и имеют как пря-

м ое, так и обратное передаточное отношение: