Пример 1.5 (см. Условие к рис. 1.2)

Определим Q₁ и Q₂, соответствующие обобщенным координатам x_D и x_A (рис. 1.6,а).

На систему действуют три активные силы: P_A = 2P, P_B = P_D =P.

Рис. 1.6

Определение Q₁. Дадим системе первое возможное перемещение, когда x_D > 0, x_A = 0 (рис. 1.6,а). При этом груз D переместится по вертикали вниз на расстояние x_D, блок B повернется против часовой стрелки на угол _B, ось цилиндра A останется неподвижной, цилиндр A повернется вокруг оси A на угол _A по часовой стрелке. Составим сумму работ на указанных перемещениях:

;

определим

. (в)

Определим Q₂. Дадим системе второе возможное перемещение, когда x_D = 0, x_A > 0 (рис. 1.6,б). При этом ось цилиндра A переместится по вертикали вниз на расстояние x_A, цилиндр A повернется вокруг оси A по часовой стрелке на угол _A, блок B и груз D останутся неподвижными. Составим сумму работ на указанных перемещениях:

;

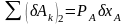определим

. (г)

Пример 1.6 (см. Условие к рис. 1.3)

Определим Q₁ и Q₂, соответствующие обобщенным координатам , s (рис. 1.7,а). На систему действуют четыре активные силы: вес стержня P, вес шарика , силы упругости пружины и .

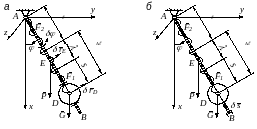
Рис. 1.7

Учтем, что . Модуль сил упругости определяется по формуле (а).

Отметим, что точка приложения силы F₂ неподвижна, поэтому работа этой силы на любом возможном перемещении системы равна нулю, в выражение обобщенных сил сила F₂ не войдет.

Определение Q₁. Дадим системе первое возможное перемещение, когда  > 0, s = 0 (рис. 1.7,а). При этом стержень AB повернется вокруг оси z против часовой стрелки на угол , возможные перемещения шарика D и центра E стержня направлены перпендикулярно отрезку AD, длина пружины не изменится. Составим в координатной форме [см. формулу (1.3б)]:

.

(Обратим внимание на то, что 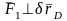, поэтому работа этой силы на первом возможном перемещении равна нулю).

Выразим перемещения x_E и x_D через . Для этого вначале запишем

, .

Затем в соответствии с формулой (7) прил. 1 найдем

, .

Подставляя найденные величины в , получим

.

По формуле (1.4), учитывая, что 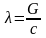, определим

. (д)

Определение Q₂. Дадим системе второе возможное перемещение, когда  = 0, s > 0 (рис. 1.7,б). При этом стержень AB останется неподвижным, а шарик M сместится вдоль стержня на расстояние s. Составим сумму работ на указанных перемещениях:

;

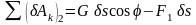определим

;

подставив значение силы F₁ из формулы (а), получим

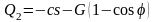. (е)

1.5. Выражение кинетической энергии системы в обобщенных координатах

Кинетическая энергия системы равна сумме кинетических энергий ее тел и точек (прил. 2). Чтобы получить для T выражение (1.2), следует скорости всех тел и точек системы выразить через обобщенные скорости, используя методы кинематики [2]. При этом система считается находящейся в произвольном положении, все ее обобщенные скорости считаются положительными, т. е. направленными в сторону возрастания обобщенных координат.

Пример 1.7 (см. Условие к рис. 1.1)

Рис. 1.8

Определим кинетическую энергию системы (рис. 1.8), взяв в качестве обобщенной координаты расстояние s,

T = T_A + T_B.

По формулам (2) и (3) прил. 2 имеем: .

Далее выразим V_A и _B через : .

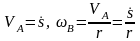Подставляя эти данные в T и учитывая, что , получим

. (ж)

Пример 1.8 (см. условие к рис. 1.2)

Рис. 1.9

Определим кинетическую энергию системы на рис. 1.9, взяв в качестве обобщенных координат величины x_D и x_A,

T = T_A + T_B + T_D.

По формулам (2), (3), (4) прил. 2 запишем

.

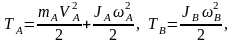
Выразим V_A, V_D, _B и _A через :

.

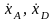При определении _A учтено, что точка O (рис. 1.9) – мгновенный центр скоростей цилиндра A и V_k = V_D (см. соответствующие пояснения к примеру 2 прил. 2).

Подставляя полученные результаты в T и учитывая, что

,

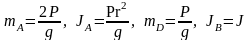определим

. (и)

Рис. 1.10

Пример 1.9 (см. условие к рис. 1.3)

Определим кинетическую энергию системы на рис. 1.10, взяв в качестве обобщенных координат  и s,

T = T_AB + T_D .

По формулам (1) и (3) прил. 2 имеем

Выразим _AB и V_D через и :

,

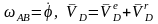где 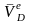– переносная скорость шарика D, ее модуль определяется формулой

,

направлена перпендикулярно отрезку AD в сторону возрастания угла ; – относительная скорость шарика, ее модуль определяется по формуле , направлена в сторону возрастания координаты s. Заметим, что перпендикулярна , поэтому

.

Подставляя эти результаты в T и учитывая, что

,

получим

. (к)