Пример 1.1 (рис. 1.1)

В качестве обобщенной координаты системы можно выбрать координату s точки A, отсчитываемую вдоль линии ее движения от какой-либо неподвижной точки на этой линии в направлении движения точки A.

Если бы по условию задачи требовалось определить угловое ускорение барабана B, то в качестве обобщенной координаты системы следовало взять угол  поворота барабана, отсчитываемый от какого-либо начала отсчета в направлении вращения барабана.

Пример 1.2 (рис. 1.2)

Предполагая, что точки A и D движутся вниз, в качестве обобщенных координат системы следует взять x_A и x_D, отсчитываемые от оси y вниз. Если в результате решения задачи окажется, что 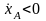(или ), то это будет означать, что точка A (или D) движется вверх.

Пример 1.3 (рис. 1.3)

Эта система имеет положение статического равновесия, в котором стержень AB совпадает с осью x, а сила тяжести G шарика D уравновешена силой упругости пружины. Напомним, что сила упругости пружины , где c – коэффициент жесткости пружины, – ее деформация в произвольном положении шарика D;  – деформация пружины в положении статического равновесия системы. Учитывая, что  = G / c, получим

F = G + cs. (а)

В качестве обобщенных координат системы в данном примере следует взять угол  поворота стержня AB и расстояние s шарика D от его положения, в котором деформация пружины равна .

1.4. Определение обобщенных сил

1.4.1. Обобщенная сила системы с одной степенью свободы

Для системы с одной степенью свободы обобщенной силой, соответствующей обобщенной координате q, называют величину, определяемую формулой

, (1.3)

где q – малое приращение обобщенной координаты; – сумма элементарных работ сил системы на ее возможном перемещении.

Напомним, что возможное перемещение системы определяется как перемещение системы в бесконечно близкое положение, допускаемое связями в данный момент времени (подробнее см. прил. 1).

Известно, что сумма работ сил реакций идеальных связей на любом возможном перемещении системы равна нулю. Поэтому для системы с идеальными связями в выражении следует учитывать только работу активных сил системы. Если же связи не идеальны, то силы реакций их, например, силы трения, условно считаются активными силами (см. ниже указания к схеме на рис. 1.5). В включается элементарная работа активных сил и элементарная работа моментов активных пар сил. Запишем формулы для определения этих работ. Допустим, сила (F_kx,F_ky,F_kz) приложена в точке К, радиус-вектор которой есть 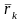(x_k,y_k,z_k), а возможное перемещение – (x_k,y_k,z_k). Элементарная работа силы на возможном перемещении равна скалярному произведению , которому в аналитической форме соответствует выражение

А( ) = F_к r_к cos( ), (1.3а)

а в координатной форме – выражение

А( ) = F_kx x_k + F_ky y_k + F_kz z_k. (1.3б)

Если пара сил с моментом М приложена к вращающемуся телу, угловая координата которого есть , а возможное перемещение , то элементарная работа момента М на возможном перемещении  определяется по формуле

А(М) =  M . (1.3в)

Здесь знак (+) соответствует случаю, когда момент М и возможное перемещение  совпадают по направлению; знак (–), когда они противоположны по направлению.

Чтобы можно было по формуле (1.3) определить обобщенную силу, надо возможные перемещения тел и точек в выразить через малое приращение обобщенной координаты q, используя зависимости (1)…(7) прил. 1.

Определение обобщенной силы Q, соответствующей выбранной обобщенной координате q, рекомендуется производить в следующем порядке.

• Изобразить на расчетной схеме все активные силы системы.

• Дать малое приращение обобщенной координате q > 0; показать на расчетной схеме соответствующие возможные перемещения всех точек, в которых приложены силы, и возможные угловые перемещения всех тел, к которым приложены моменты пар сил.

• Составить выражение элементарной работы всех активных сил системы на этих перемещениях, возможные перемещения в выразить через q.

• Определить обобщенную силу по формуле (1.3).