
- •Дифференциальное уравнение движения.
- •Решение прямой задачи.
- •Решение обратной задачи.
- •Дифференциальные уравнения движения точки в естественной форме
- •4.Теорема об изменении количества движения точки.
- •Теорема (в дифференциальной форме)
- •5.Теорема об изменении кинетического момента системы относительно неподвижной оси
- •6. Момент инерции тела относительно оси. Радиус инерции. Теорема Гюйгенса.
- •8. Теорема об изменении кинетической энергии механической системы.
- •12. Принцип Даламбера-Лагранжа. Общее уравнение динамики.
- •13. Обобщенные координаты. Обобщенные силы, их вычисление.
- •14. Уравнения Лагранжа.
- •1. Уравнения лагранжа второго рода
- •1.1. Общие указания
- •Пример 1
- •Пример 2
- •1.2. Определение числа степеней свободы системы
- •1.3. Выбор обобщенных координат
- •Пример 1.1 (рис. 1.1)
- •Пример 1.2 (рис. 1.2)
- •Пример 1.3 (рис. 1.3)
- •1.4. Определение обобщенных сил
- •1.4.1. Обобщенная сила системы с одной степенью свободы
- •Пример 1.4 (см. Условие к рис. 1.1).
- •1.4.2. Определение обобщенных сил системы с двумя степенями свободы
- •Пример 1.5 (см. Условие к рис. 1.2)
- •Пример 1.6 (см. Условие к рис. 1.3)
- •1.5. Выражение кинетической энергии системы в обобщенных координатах
- •Пример 1.7 (см. Условие к рис. 1.1)
- •1.6. Составление дифференциальных уравнений движения механических систем
- •Пример 1.10
- •Пример 1.11
- •Пример 1.12
- •1.7. Методика решения задач с помощью уравнений Лагранжа
- •Замечания
- •2. Уравнения Лагранжа для консервативных систем
- •2.1. Общие указания
- •2.2. Проверка системы на консервативность
- •2.3. Определение потенциальной энергии системы
- •2.4. Составление дифференциальных уравнений движения консервативных систем
- •2.5. Методика решения задач с помощью уравнений Лагранжа для консервативных систем
12. Принцип Даламбера-Лагранжа. Общее уравнение динамики.
Формулировка принципа: при движении механической системы с идеальными связями сумма работ всех активных сил и сил инерции на любом возможном перемещении равна нулю.


Это положение носит также название общего уравнения динамики системы.
13. Обобщенные координаты. Обобщенные силы, их вычисление.
Обобщенными координатами называются независимые между собой переменные параметры системы, которые однозначно определяют положение тел и точек этой системы в любой момент времени. В качестве обобщенных координат обычно выбирают углы поворота тел системы или координаты ее точек.
Для системы с одной степенью свободы обобщенной силой, соответствующей обобщенной координате q, называют величину, определяемую формулой
 ,
(1.3)
,
(1.3)
где dq –
малое приращение обобщенной координаты; ![]() –
сумма элементарных работ сил системы
на ее возможном перемещении.
–
сумма элементарных работ сил системы
на ее возможном перемещении.
Определение обобщенной силы Q, соответствующей выбранной обобщенной координате q, рекомендуется производить в следующем порядке.
· Изобразить на расчетной схеме все активные силы системы.
· Дать малое приращение обобщенной координате dq > 0; показать на расчетной схеме соответствующие возможные перемещения всех точек, в которых приложены силы, и возможные угловые перемещения всех тел, к которым приложены моменты пар сил.
· Составить выражение элементарной работы всех активных сил системы на этих перемещениях, возможные перемещения в выразить через dq.
· Определить обобщенную силу по формуле (1.3).
14. Уравнения Лагранжа.
1. Уравнения лагранжа второго рода
1.1. Общие указания
Уравнения Лагранжа второго рода (далее – уравнения Лагранжа) представляют собой дифференциальные уравнения движения системы в обобщенных координатах [1].
Обобщенные координаты – независимые между собою переменные параметры системы, однозначно определяющие положение системы в любой момент времени. Число обобщенных координат системы с голономными связями*) (ниже рассматриваются только такие системы) равно числу ее степеней свободы.
Уравнения Лагранжа имеют вид
 ,
i = 1, 2,…,n,
(1.1)
,
i = 1, 2,…,n,
(1.1)
где
n – число степеней
свободы голономной системы, qi
– обобщенные координаты,
 – обобщенные скорости (производные
обобщенных координат по времени t),
Qi
– обобщенные силы, T
– кинетическая энергия системы,
– обобщенные скорости (производные
обобщенных координат по времени t),
Qi
– обобщенные силы, T
– кинетическая энергия системы,
 и
и
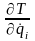 – частные производные кинетической
энергии системы по обобщенной координате
qi
и по обобщенной скорости
,
– частные производные кинетической
энергии системы по обобщенной координате
qi
и по обобщенной скорости
,
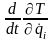 – производная
по времени t.
– производная
по времени t.
Кинетическую энергию системы со стационарными связями**) (ниже рассматриваются системы именно с такими связями) целесообразно до подстановки в уравнения (1.1) представить в виде функций обобщенных координат и обобщенных скоростей
 .
(1.2)
.
(1.2)
Чтобы из уравнений Лагранжа (1.1) получить дифференциальные уравнения движения системы, нужно уметь:
устанавливать число степеней свободы системы (подразд. 1.2),
выбирать ее обобщенные координаты (подразд. 1.3),
определять обобщенные силы (подразд. 1.4),
составлять выражение кинетической энергии системы в обобщенных координатах (подразд. 1.5).
Выполнение этих операций будем рассматривать на следующих трех примерах.
