1. Дифференциальное уравнение движения.

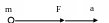Пусть на материальную точку m действует сила F. По второму закону эта точка получит ускорение, по модулю пропорциональное модулю силы в направление этой же силы. Запишем основное уравнение динамики.

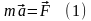
Проецируем это уравнение на оси координат , где а_x, a_y, a_z – проекции ускорения на оси координат x, y, z, соответственно.

F_x, F_y, F_z – проекции сил. Учитывая:

Перепишем систему (2) с учётом (3):

Системы (2), (4), (5) представляют собой дифференциальные уравнения движения материальной точки в проекциях на оси координат.

Решение прямой задачи.

Первая задача считается заданной, если известно уравнение движения материальной точки, массой m.

Решение обратной задачи.

Решение обратной задачи на теории интегрального исчисления. Задача считается заданной, если задана масса материальной точки и силы, действующие на эту точку. По заданным силам и массе определяют уравнение движения. Используя дифференциальное уравнение в системах (2),(4),(5). Пусть задана масса и сила. При решении обратной задачи вводятся понятия “начальное условие”. К начальному условию в механике относятся две величины “положение материальной точки и скорость”, в момент рассмотрения задачи, т.е. в момент рассмотрения задачи, т.е. в момент, когда время отсчёта равно 0, т.е. при 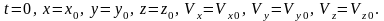- Начальное условие.

2. Дифференциальные уравнения движения точки в естественной форме

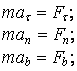      или                                       (1.3)

где   – проекции ускорения   на естественные оси координат;   – дуговая координата точки;   – скорость точки;   – радиус кривизны траектории;   – проекции силы   на естественные оси координат.

С помощью дифференциальных уравнений (1.2) и (1.3) можно решить любую задачу динамики свободной материальной точки.

3. Уравнения относительного движения материальной точки

    Уравнение второго основного закона динамики для абсолютного движения точки массой m имеет вид

где a – абсолютное ускорение точки;

     F_i – силы, действующие на точку, включая реакции связей.

    Абсолютное ускорение точки в сложном движении определяется как геометрическая сумма трех ускорений: переносного a_пер , относительного a_отн  и кориолисова a_кор ,  т.е. 

    Подставляя это выражение в (7.1), получим

или 

    Введем в рассмотрение два вектора

и назовем их переносной и кориолисовой силами инерции.

    

Подставим эти векторы в уравнение (7.2):

    Уравнение (7.3) представляет собой основное уравнение динамики  относительного движения материальной точки. 

4.Теорема об изменении количества движения точки.

Теорема об изменении количества движения точки (K), называется векторная величина, равная произведению векторной скорости точки.

Теорема (в дифференциальной форме)

Производная по времени от количества движения точки равна сумме действующих на точку сил

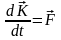
Доказательство:

5.Теорема об изменении кинетического момента системы относительно неподвижной оси

 

Формулировка теоремы: производная по времени от кинетического момента системы относительно неподвижной оси   равна сумме моментов всех внешних сил относительно этой оси, т. е.

.                                         (2.4)

Рассмотрим методику решения задач с помощью этой теоремы:

– изображаем систему в произвольный момент времени, показывая все внешние силы, действующие на систему;

– находим сумму моментов внешних сил относительно оси;

– находим кинетический момент системы относительно оси;

– находим производную по времени от кинетического момента системы;

– составляем уравнение (2.4);

– решаем это уравнение, находим искомые величины.