31. Кінцеві характеритики се у глобальній системі координат.

Кінцеві переміщення і кінцеві реакції в глобальній системі координат можуть бути представлені у вигляді векторів

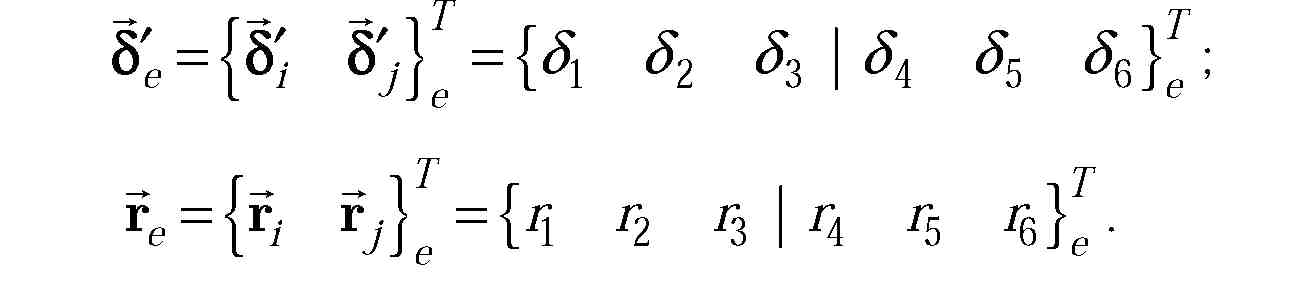
для стержня жорстко прикріпленого до вузлів

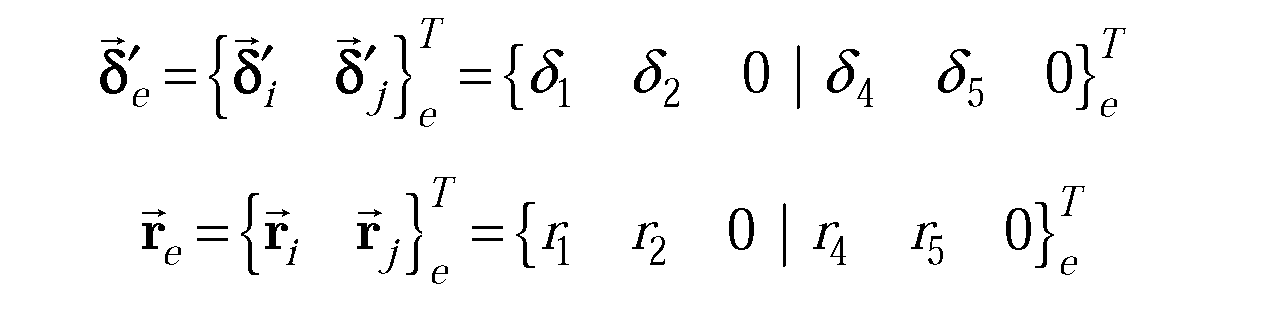
Між кінцевими характеристиками в глобальній та в локальній системах координат може бути встановлений формальний зв’язок:

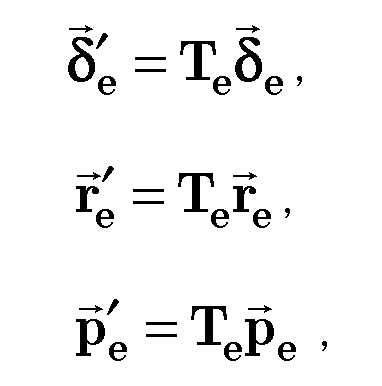
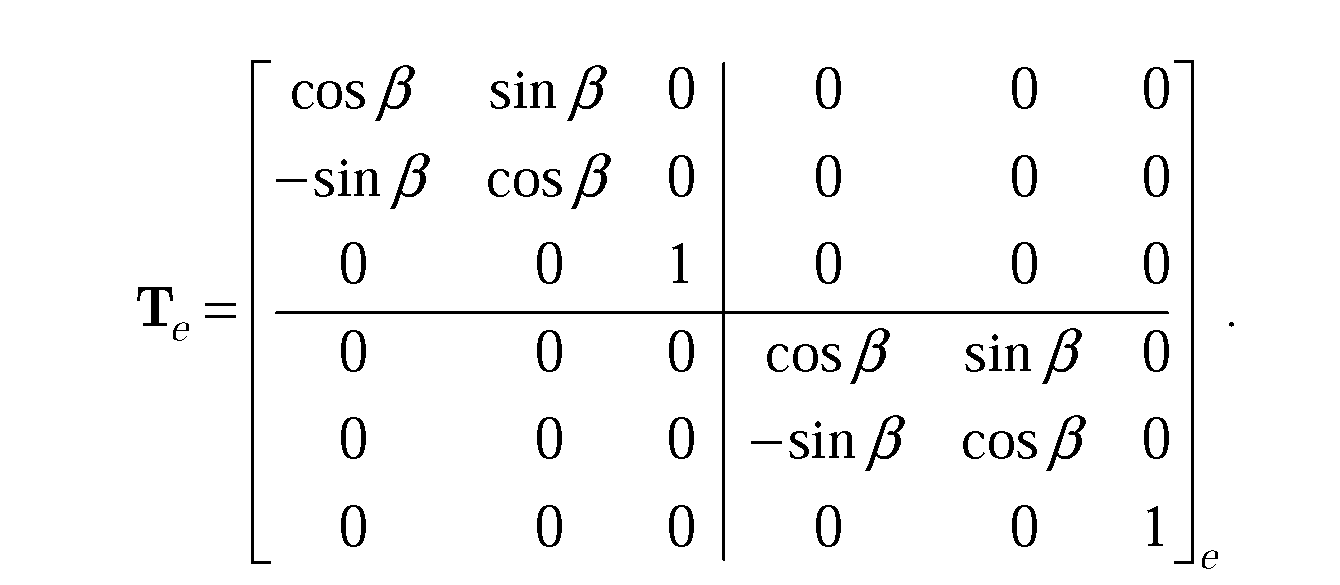
Квадратна матриця називається матрицею перетворення стержневого елемента e.

32. Зв'язок між кінцевими характеристиками стержнів. Матриця перетворень.

Між кінцевими характеристиками в глобальній та в локальній системах координат може бути встановлений формальний зв’язок:

Квадратна матриця називається матрицею перетворення стержневого елемента

33.Матриця жорсткості

Стержень із затисненням на обох кінцях.

Маємо такі граничні умови :

При х=0

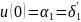
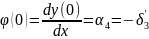
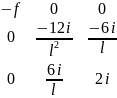
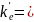
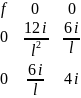
Вектор вантажних реакцій при цьому:

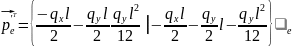
Стержень із затисненням на початку і шарніром на кінці:

За формулами знаходимо коефіцієнти матриці жорсткості і елементи вектора вантажних реакцій:

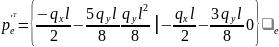
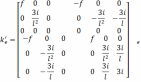
Стержень із шарніром на початку і з затисненням на кінці: Матриця жорсткості і вектор вантажних реакцій стержня:

С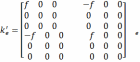 тержень із шарнірами з обох сторін

Матриця жорсткості стержня і вектор вантажних реакцій:

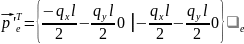
34. Матриця жорсткості

Матриця жорсткості стержня в локальних системах координат визначають величини кінцевих реакцій, які орієнтовані за осями локальних систем координат. При розгляді сумарної дії стержнів на вузли скінченноелементної моделі виникає необхідність привести всі ці реакції, що передаються на вузли з боку стержнів, до спільних напрямів. За ці напрями доцільно обрати напрями осей глобальної системи координат всієї моделі. Отже, постає задача перетворення кінцевих реакцій стержня з локальної у глобальну систему координат, тобто задача побудови матриць жорсткості стержнів у глобальній системі координат.

Матричний вираз може бути представлений співвідношенням:

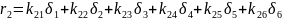
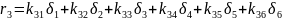
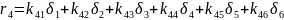
Таким чином, матриця жорсткості стержня в глобальній (загальній) системі координат має вигляд:

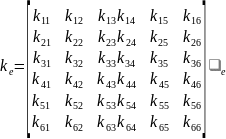
35 Матриця жорсткості скінченноелементної моделі. Фізичний зміст елементів матриці

З умов рівноваги будь-якого вузла i, жорсткого (рис.6.18,а) або шарнірного (рис.6.18,б) маєм о:

а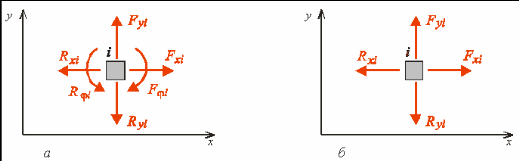 бо в матричній формі: Fi-Ri=0. Отже, для всіх вузлів скінченноелементної моделі можна записати F-R=0 або R-F=0 ( 6.43 )

Вузлові реакції, що зумовлені переміщеннями вузлів, для лінійно-деформованих систем можуть бути представлені виразами:

У матричній формі лінійне перетворення може бути записане у вигляді: R=K∆ (6.45), де K- матриця жорсткості всієї скінченноелементної моделі:

Довільний коефіцієнт Ki, j являє собою вузлову реакцію Ri , що викликана вузловим перемі-

щенням : j = 1, за умови, що всі інші переміщення вузлів дорівнюють нулю. Головні коефіцієнти матриці жорсткості являють собою додатні числа (Ki,i >0). Побічні коефіцієнти симетричні відносно головної діагоналі, тобто Ki, j = K j,i .Підставивши (6.45) у рівняння рівноваги (6.43), одержимо: K∆-F=0

Т акі самі рівняння в координатній формі представлятимуться співвідношеннями:

Невідомими в рівняннях (6.48) є переміщення вузлів, коефіцієнти - величини вузлових реак-

цій, вільні члени - вузлові навантаження. будь-який коефіцієнт матриці жорсткості скінченноелементної моделі Ki, j являє собою вузлову реакцію Ri , що зумовлена вузловим переміщенням D j = 1. На цій підставі для обчислення коефіцієнтів матриці жорсткості необхідно почергово надавати одиничні переміщення вузлам скінченноелементної моделі і знаходити сили, які передаватимуться при цьому на вузли. Величини цих сил визначаються елементами відповідних матриць жорсткості окремих скінченних елементів.