- •Поняття про статичну невизначуваність
- •2.Основні властивості статично невизначуваних систем:
- •4.Основна система методу сил способи відкидання зайвих вязей
- •5. Система канонічних рівнянь методу сил.
- •6. Обчислення коеф. Системи канонічних рівнянь методу сил
- •7. Побудова і перевірка дійсних епюр зусиль в методі сил.
- •8.Обчислення переміщень в статично невизначуваних системах.
- •9. Групування основних невідомих в методі сил
- •10) Розрахунок симетричних рам методом сил
- •11) Розрахунок нерозрызних балок
- •12. Метод момент них фокусів
- •13. Розрахункові зусилля.
- •16.Особливості розрахунку статично невизначуваних комбінованих систем
- •17) Метод переміщень. Основні передумови розрахунку
- •18). Основні невідомі методу переміщень
- •19). Основна система методу переміщень
- •20) Розв’язувальні рівняння методу переміщень
- •21. Обчислення коефіцієнтів системи канонічних рівнянь методу переміщень.
- •22.Побудова і перевірка дійсних епюр зусиль в методі переміщень
- •23. Групування основних невідомих методу переміщень
- •25. Розгорнута форма методу переміщень
- •26. Змішаний метод
- •27. Дискретна модель стержневої системи. Типи скінченних елементів.
- •28. Глобальна і локальна системи координат. Зв’зок між ними.
- •29. Вузлові характеристики.
- •30. Кінцеві характеристики скінченних елементів
- •31. Кінцеві характеритики се у глобальній системі координат.
- •32. Зв'язок між кінцевими характеристиками стержнів. Матриця перетворень.
- •33.Матриця жорсткості
- •34. Матриця жорсткості
- •35 Матриця жорсткості скінченноелементної моделі. Фізичний зміст елементів матриці
- •3 6 Обчислення внутрішніх зусиль у методі скінченних елементів
- •37. Теорема Кастільяно.
- •38. Теорема Лагранжа
29. Вузлові характеристики.
Вузловими
скінченноелементної моделі можуть
бути охарактеризовані як зі статичного,
так і з кінематичного боку. Кінематичними
характеристиками є вузлові переміщення,
а статичними – вузлові реакції і вузлові
навантаження. Будь-який вільний жорсткий
вузол і
скінченноелементної моделі має три
ступні вільності, тобто можливість двох
поступальних і одного кутового переміщень
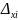 ,
,
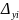 ,
,
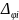 цього вузла. Зазначені величини можуть
бути записані у вигляді вектора
цього вузла. Зазначені величини можуть
бути записані у вигляді вектора
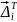 =
=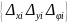 .
Шарнірний вузол має два ступені вільності
і, відповідно, вектор переміщень такого
вузла матиме два компонента:
.
Шарнірний вузол має два ступені вільності
і, відповідно, вектор переміщень такого
вузла матиме два компонента:
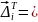
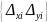 .
сукупність всіх вузлових переміщень
скінченноелементної моделі становить
вектор вузлових переміщень:
.
сукупність всіх вузлових переміщень
скінченноелементної моделі становить
вектор вузлових переміщень:
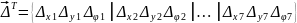
Вузлові
реакції всієї скінченноелементної
моделі утворюють вектор вузлових
реакцій:
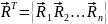 .
при розв’язуванні практичних задач
використовується наскрізна нумерація
реакцій, причому їхні номери повинні
збігатися з номерами відповідних
переміщень:
.
при розв’язуванні практичних задач
використовується наскрізна нумерація
реакцій, причому їхні номери повинні
збігатися з номерами відповідних
переміщень:
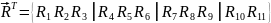 .
.
Іншою
статичною характеристикою вузлів
скінченноелементної моделі є вузлові
навантаження. У кожному вузлі припускається
можливість дії трьох компонентів
зовнішніх зосереджених силових дій:
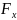 - сила, спрямована вздовж осі х глобальної
системи координат;
- сила, спрямована вздовж осі х глобальної
системи координат;
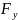 - сила, яка діє вздовж осі у;
- сила, яка діє вздовж осі у;
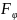 - зосереджений момент. Зосереджені дії
у вузлі і
можуть бути записані у вигляді вектора:
- зосереджений момент. Зосереджені дії
у вузлі і
можуть бути записані у вигляді вектора:
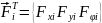 ,
а сукупність зведених до вузлів
скінченноелементної моделі навантажень
– у вигляді вектора
,
а сукупність зведених до вузлів
скінченноелементної моделі навантажень
– у вигляді вектора
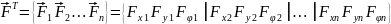 .
.
30. Кінцеві характеристики скінченних елементів
У процесі деформування споруди її вузли і, отже, кінці стержнів переміщуються, внаслідок чого на кінцях виникають реакції взаємодії стержнів з вузлами скінченноелементної моделі. Означені реакції і переміщення можуть бути визначені або в глобальній, або в локальній системі координат.
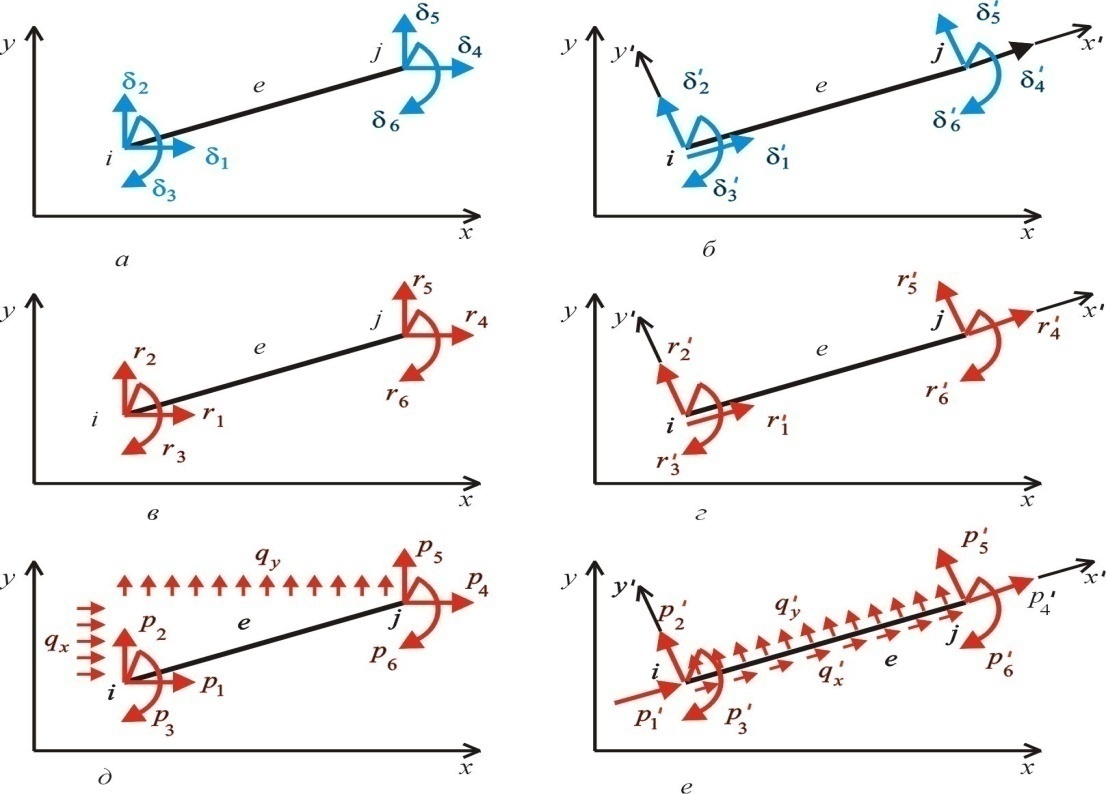
Кінцеві переміщення і реакції також можуть бути подані у вигляді компонентів, які являють собою проекції відповідних величин на осі локальної системи координат (рис.6.4,г,д,е). Нумерація кінцевих реакцій також строго фіксована й аналогічна нумерації кінцевих переміщень в глобальній системі координат. Так, для кінцевих переміщень у локальній системі координат використовують позначення, наведені (табл.)
Напрям переміщення |
Вздовж осі х’ |
Вздовж осі y’ |
Кут повороту
|
На початку і
|
1 |
2 |
3 |
На кінці j |
4 |
5 |
6 |
Те = {і j }е = {1 2 3 | 4 5 6}е
reТ = { rі rJ}е= { r1 r2 r3 | r4 r5 r6 }е
рeТ ={ рі рJ}е = { р1 р2 р3| р4 р5 р6 }е
Розподілені на стержневому скінченному елементі. навантаження, можуть бути орієнтовані за осями локальної системи координат даного елемента
Навантаження, орієнтоване по глобальним осям координат, може бути перетворене у наван-
таження, орієнтоване по локальній системі координат, за формулами
qx=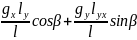
qy=