1. Случайные события, и действия над ними. Событием называется любой факт, который в результате опыта может произойти или не произойти. Примеры случайных событий: выпадение шестерки при подбрасывании игральной кости, отказ технического устройства, искажение сообщения при передаче его по каналу связи. С событиями связываются некоторые числа, характеризующие степень объективной возможности появления этих событий, называемые вероятностями событий.

Достоверным называется событие, которое происходит в каждом опыте.

Невозможным называется событие, которое в результате опыта произойти не может.

Несовместными называются события, которые в одном опыте не могут произойти одновременно.Суммой (объединением) двух событий A и B (обозначается A+B, AÈB) называется такое событие, которое заключается в том, что происходит хотя бы одно из событий, т.е. A или B, или оба одновременно.Произведением (пересечением) двух событий A и B (обозначается A×B, AÇB) называется такое событие, которое заключается в том, что происходят оба события A и B вместе.Противоположным к событию A называется такое событие, которое заключается в том, что событие A не происходит.

События Ak (k=1, 2, ..., n) образуют полную группу, если они попарно несовместны и в сумме образуют достоверное событие. Действия над ними: А+В называется событие С, состоящее в наступлении хотя бы одного из них вместе. АхВ наз-ся событие С, состоящая в совместном наступлении событий. А-В = С, происходит событие А, но не происходит событие В. Противоположным к событию A называется такое событие, которое заключается в том, что событие A не происходит.

При преобразовании выражений можно пользоваться следующими тождествами:

2. Определение вероятности и ее свойства.

Классическое определение вероятности: вероятность события определяется по формуле

, где n - число всех событий;

m - число благоприятных событий.

С в о й с т в а: 1. Вероятность достоверного события равна единице.Действительно, если событие достоверно, то каждый элементарный исход испытания благоприятствует событию. В этом случае m = n, следовательно,Р (A) = m / n = n / n = 1. 2. Вероятность невозможного события равна нулю. Действительно, если событие невозможно, то ни один из элементарных исходов испытания не благоприятствует событию. В этом случае m = 0, следовательно, Р (А) = m / n = 0 / n = 0. 3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей. Действительно, случайному событию благоприятствует лишь часть из общего числа элементарных исходов испытания. В этом случае 0 < m < n, значит, 0 < m / n < 1, следовательно,

0 < Р (А) < 1. Итак, вероятность любого события удовлетворяет двойному неравенству

0 <= Р (A) < 1.

 

3. Элементы комбинаторики. Комбинаторика – раздел математики, изучающая задачи выбора элементов из определенного множества и распред-е их по группам по заданным правилам. Рассмотрим некоторое множество Х, состоящее из n элементов . Будем выбирать из этого множества различные упорядоченные подмножества из k элементов.Размещением из n элементов множества Х по k элементам назовем любой упорядоченный набор элементов множества Х.Если выбор элементов множества из Х происходит с возвращением, т.е. каждый элемент множества Х может быть выбран несколько раз, то число размещений из n по k находится по формуле (размещения с повторениями).Если же выбор делается без возвращения, т.е. каждый элемент множества Х можно выбирать только один раз, то количество размещений из n по k обозначается и определяется равенством (размещения без повторений).Частный случай размещения при n=k называется перестановкой из n элементов. Число всех перестановок из n элементов равно . Пусть теперь из множества Х выбирается неупорядоченное подмножество (порядок элементов в подмножестве не имеет значения). Сочетаниями из n элементов по k называются подмножества из k элементов, отличающиеся друг от друга хотя бы одним элементом. Общее число всех сочетаний из n по k обозначается и равно .Справедливы равенства: , , .1. Правило умножения. Если объект Х можно выбрать из совокупности объектов n1 способами и после каждого такого выбора объект У можно выбрать n2 способами, то пара объектов (Х, У) в указанном порядке может быть выбрана m*n способами. 2. Правило суммы: Если некоторый объект Х может быть выбран из совокупности объектов n1 способами, а другой объект У может быть выбран n2 способами, то выбрать либо А, либо В можно m + n способами.

4. Условная вер-ть. Предположим, что из общего числа n исходов исп-я событию А благоприятствуют m элементарных исходов, событию B благоп. к элемен-х исходов, а одновременному наступлению событий А и В благоприп. l элем. исходов. Если событие В наст.,это означает что один из к благоприпт. исходов, причем этих к способов благоприя. событию А те же l исходов, при которых Аи В наступит одновременно. Отсюда следует, что вер-ть Р (А/В) или Р_в (А) собития А при условии, что наступило событие В . Р( А/В) = (l/n) / (k/n) = P (AB) / P ( B). При статест. определении вер-ти равенство P (AB) / P ( B) принимается за определение условий вер-ти, при условии Р(В) не равное 0. Т.о. условной вер-тью Р (А/В) наз-ся вер-ть события вычисленную а предположеии, что собитие В наступило. Условной вер-тью Р (В/А) вер-ть события в предположении,что А наступило. Одним из основных понятий ТВ, является понятие независимости событий: 2 события наз-ся незави-ми, если вер-ть одного из них не зависит от наступления или ненаступления другого события. Понятие назав-ти вводится любого числа n больше 2х событий. Собития а1, а2…аn наз-ся независимыми в соотв-ии если каждое из этих чисел собитий независимо в паре с любыми произведениям остальных событий.

5. Вероятности произведения и суммы событий. Тео-а сложения вер-ти. События состоящие в том,что наступило хотя бы одно из событий А или В, или оба эти события, наз-ся суммой 2х соб-й, и обозначаются символом А+В, в том случаи если события А и В - несовместимые, то сума А+В - это событие состоящее появлении одного из этих событий. Теорема: вер-ть наступления одного из 2х несов-х событий равна сумме вер-ти этих событий. Р (А+В) = Р(А) +Р(В). Следствие: вер-ть наступления одного или неск-х попарно не совместных событий равна сумме вер-ти этих событий: Р (А1+А2+..+Аn)= Р(А1)+Р(А2)..+Р(Аn). Полная группа событий это сов-ть единственно возможных событий, испытаний. Теорема: Вер-ть хотя бы одного из 2х совместных событий за вычитом вер-ти их одновременного наступления. Р(АВ) = Р(А) + Р(В) – Р(АВ). Теорема умножения: Произведением 2х событий А и В наз-ся событие АхВ или АВ, состоящая в одновременном наступлении события А и В. Теорма: Ве-ть одновременно 2х событий равна Р(АхВ) = Р(А) х Р(В). Следствие: вер-ть появления одновременно нес-х соб-й попарно независимых равна Р (А1 х А2…Аn) = Р ( А1) х …Р(Аn). Теорема: вер-ть появления хотя бы одного из события А1, А2, Аn, независимых в сов-ти равна разности между 1 и произведением вероятности противоп-х событий. Р(А) = 1- q1 * q2* …* qn. Теорема вер-ти зависимых событий: Вер-ть одновременного появления 2х независимых событий равна произведению вер-ти одного их них на условную вер-ть другого, расчитаную пр и условии, что 1 соб. уже наступило: Р(АВ) = Р(А) * Р(В/А)

6. Полная ве-ть. Пусть имеется группа событий В1, В2…Вn, обладающая св-вами: 1) все события по парно не совместны. 2) Их объедениеи образут про-ство элементр. исходов Q= В1 U B2… События В1,..,Вn образует полную группу событий, такие события так же называ-ся гипотезами, поскольку за ранее неизвестно, какой и этих событий наступит. Пусть А – некторое событие, которое может произойти при наступлении одного и только одно из событий В1..Вn? это означает, что А= А х В1 + А х В2 + А х Bn. Теорема: Ве-ть события А,которое может наступить лишь при условии появления одно из несовм. событий В1, В2, Вn, образующих полную группу, равна сумме произведения вер-ти, каждого из этих событий на соот. услов. вер-ти собития А формулой полной вер-ти. P (A)=Р (В1)хР(А/В1) + Р (В2) х Р(А/В2)..+Р(Вn/Аn)

7. Фор-а Байеса. Пусть имеется событие А, которое может произойти одно и только одно событие В1, …Вn из некоторой полной группы по парнонесовмест. Событий. Необходимо найти вероятность событие B_i , при условии что событие А уже наступило. По т. умнож-я Р ( B_i*A) - ( B_i/A)= Р ( B_i) * (A/B_i) , отсюда следует что Р(B_i/A) =[ Р ( B_i) * P(A/B_i) ] / Σ P (B_j) * P(A/B_J) где, j = 1,2,…, n

8. Неза-е испыт-я. Формула Бернулли. Опыт наз-ся независимым, если их исход независим. После-ть к независимых испытаний, в которых может произойти событие А . Р(А)=р или противоположно событию Ā ;Р(Ā) = 1-р=q ; Р(А) + Р(Ā.) = 1.

Если имеется большое кол-во испытании, и Р (Ā) = 1-р=q это схема Бернулли. Р (Ā, Ā₁, А) = (1-р)(1-р)р = q²р. Формула Бернулли. Пусть есть n неза-х испыт-й, в которых собитые А наступает m раз. Вер-ть событий записывается:

9. Предельные теоремы в схеме Бернулли. Теорема Пуассона. Если число испытаний увел.

(n →∞) и вер-ть р события А, в каждом испытании стремится к 0 (р→0), причем np= const, то вер-ть будет

Локальная и интегральная теоремы. Если вер-ть наступления события постоянно р= const и отлична от 0, а число неза-х испытаний достаточно велико, то вер-ть приближенно

,где: , -- кривая Гаусса.

Интегральная: если вер-ть р в наступлении события А в каждом испытании постоянна и отлична от 0 и 1, то вер-ть наступления n, вычисляется по формуле приближенно вычисляется формулой:

, где - функция Лапласа,

, _/

Теорема Пуассона

х	х1	х2
р	р1	р2

10. Случайная величина. Закон распределения СВ. СВ- величина, которая принимает какое- либо значение в результате опыта за ранее неизвестного. СВ принимающая конечное счетное множество значений называется дискретной. Существует так же непрерывная СВ, когда множество значение несчетное. СВ х наз-ся числовая функция определенная на пространстве элементарных событий А, которая каждому элементр. событию ставит в соответ. число. ω = х (ω). Закон распределения ДСВ. Этот закон может быть задан в виде табл. Эти события не совместны, их сумма равна 1.

11. Функция распределения и ее св-ва. Наиболее общей формой закона распр, пригодной для всех случ-х величин (как дискретных, так и недискретных) явл-ся функция распр.Ф р случайной величины X наз-ся вер-ть того, что она примет знач-е меньшее, чем аргумент ф-ции x: F(x)=P{X<x}.Геометрически ф р интерпретируется как вер-ть того, что случ-я точка X попадет левее заданной точки X. Из геометрической интерпретации наглядно можно вывести осн-е св-ва ф р: 1. F(x) – неубывающая функция своего аргумента, т.е. при x1 < x2; 2.F(-∞)=0; 3.F(+∞)=1; 4. P(α <X < β) = F(β) - F(α) – вер-ть того, что случ величина Х в рез-те опыта попадет на участок от α до β (вкл α) равна приращению ф р на этом участке.

12. Плотность распределения и ее св-ва. Плотностью распр (или плотностью вероятности) непрерывной случайной величины X в точке x наз-ся производная ее ф-ции распр-я в этой точке и обозначается f(x): f(x) = F’(x). График плотности распр наз-ся кривой распр. Пусть имеется точка x и прилегающий к ней отрезок dx. Вер-ть попадания с в X на этот интервал равна f(x)dx. Эта величина наз-ся элементом вер-ти. Св-ва пл р: 1.Пл р неотрицательна – f(x)≥0 ; 2. P(a<x≤b)= - вер-ть попадания с в X на произвольный уч-к (a, b] равна сумме элементарных вер-тей на этом уч-ке; 3.F(x)= – выражение ф-ции распр F(x) с в X через ее плотность; 4.Условие нормировки:  .

13.Числовые хар-ки с в (мат ожид-е, дисперсия, мода, медиана). Числовыми харак-ми с в наз-ся отдельные числ-е параметры, хар-щие отдельные черты распр. Мат ожид-е (Мо) харак-т ср взвешенное знач-е с в. Для вычисл-я м о для ДСВ каждое знач-е x_i учитывается с «весом», пропорциональным вер-ти этого знач-я: M(x) = . Для НСВ заменим отд-е знач-я x_i  непрерывно измен-ся параметром x, соответствующие вер-ти  - элементом вер-ти , а конечную сумму – интегралом: M(x)= . Св-ва м о: 1. М о неслучайной величины с равно самой величине с: M(c) = c; М о(const)=const; 2.постоянный множ-ль выносится: М(сХ)=сМ(Х); М(Х+с)=М(х)+с; 3.М(х+у)=М(х)+М(у); 4.М(ху)=М(х)М(у). Дисперсия(рассеянная)с в х – м о квадрата соответствующей центрированной с в Она хар-т степень разброса знач-й с в относительно ее м о, т.е. ширину диапазона знач-й. Dx= - для дсв; Dx=M - ; Dx= - для нсв. Св-ва: 1.D(c)=0; 2.D(cx)= D(x); 3.D(x+y)=Dx+Dy; 4.D(x+c)=Dx. D(xy)=M M - ; ср квадратич отклонение с в Х: . Мода дискретной случайной величины Mo(X) - это знач-е с в, имеющее наибольшую вер-ть. На многоугольнике распр мода - это абсцисса самой высокой точки. Бывает, что распр имеет не 1-у моду. Для нсв – это точка max(локального). Медиана(Ме) – такое знач-е с в Х, для которого верно данное равенство: Р{x< }=P{x> }= . Для дсв медиана обычно не опред-ся.

x=m	0	1	2	m	n

14.Биномиальный закон распр д с в. Наиболее распростр-й закон для ДСВ. Если дсв=0;1;2;..;n;..), с вер-ми =P{x=m}= (ф-ла Бернулли). С в Х распр по бином закону явл-ся числом успехов с вер-ью р в схеме Бернули проведения n незав-х опытов. Если требуется вычисл вер-ть не менее m успехов в n опытах, то нужно сложить все вер-ти при различ-х Х. Имеет ряд распр-я:

(0≤p≤1), q=1-p. ∑ . Числовые хар-ки: Мх=np; Dx=npq. F(x)=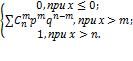

15.Распр Пуассона дсв. ДСВ имеет это расп, если ее возможное знач-е 0; 1; 2;…;m;.., а соотв вер-ти: , n ; np=a{0<a<∞}, m=0;1…Числ хар-ки: Mx=Dx=a. Закон Пуассона зависит от одного пар-ра α, смысл которого заключ-ся в сл: он явл-ся одновременно и мат ожид-м и дисперсией с в Х. Отличительная особ-ть распр – исп-ся на прак-ке, что Mх≈Dх.

x=m	0	1	2	m
Pm	p	qp	q2p	qmp

16.Геометрическое распр дсв. ДСВ X имеет геометрическое распр, если вер-ти ее возможных знач-й 0;1;2;….;m;.. определяются так: =P(x=m)= p, где p – параметр распр, (0≤р≤1), а q=1-p.

Числ харак-ки: Mx=1/p; Dx=q/p².

17.Равномерный закон распр непрерывной с в. НСВ Х равномерно распр-на в интервале [а; в], если ее плотность вер-ти в этом интервале постоянна, т.е. если все знач-я в этом интервале равновероятны: f(x)= Интегральная ф-ция вер-ти: . Ф-ция распр: 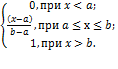. Числ хар-ки: Mx=(b+a)/2; Dx=(b-a)²/12. Равномерное распр с в полностью опред-ся 2-мя параметрами: a и b – интервалом, на котором определена с в.

18.Показательный(экспоненциальный) закон распр нсв. НСВ Х, принимающая только положительные знач-я имеет показательное (или экспоненциальное) распр, если . Положительная величина l наз-ся параметром показательного распр и полностью определяет его. Ф-цию распр с в: . Числ хар-ки: ; ; . Показательное распределение тесно связано с простейшим (стационарным пуассоновским) потоком событий.

19.Норм закон распр нсв. НСВ Х имеет норм распр, если ее плотность вер-ти имеет вид: f(x)= . Числ харак-ки: мат ожид-е: применяя замену переменной: t=(x-m)/(σ ), получим: Mx= . В полученном выраж-и 1-й интеграл равен нулю (интеграл в симметричных пределах от нечетной ф-ции), а 2-й есть интеграл Эйлера-Пуассона, т о мат ож величины Х равно m: Mx=m. Применяя замену переменной, найдем диспер: Dx= ; интегрируем по частям: Первое слагаемое в фигурных скобках равно нулю (т.к.  при t→∞ убывает быстрее, чем возрастает любая степень t), второе слагаемое равно  , откуда: Dx=σ². Т о, норм распр с в полностью описывается 2-мя числовыми харак-ми: мат ожид M[X] и ср квадратичным отклонением σ. Ф-ция Лапласа обладает сл св-ми: 1.Φ(0)=0; 2.Φ(-х)=-Φ(х); 3.Φ(-∞)=0,5. Ф-ция распр норм распределенной с в через ф-цию Лапласа выражается так: F(x)=0,5+Ф((x-m)/σ). Нормально распр с в возникает в тех случаях, когда складывается много независимых (или слабо зависимых) с в Х₁, Х₂, …, X_n. Тогда, каковы бы не были законы распр отд-х с в X_i, закон распр их суммы будет близок к норм распр.

20.Двумерная с в и ее ф-ция распр-я. Если на пространстве событий   = { } заданы 2-е случайные ф-ции X =  (W) и Y =  (W), то говорят, что задана двумерная с в (X, Y). Интегральной ф-цией распр двумерной с в (X, Y) наз-ся вер-ть совместного выполнения 2-х неравенств: X<x и Y<y: F(x,y)=P{X<x, Y<y} и геометрически опред-т вер-ть попадания случайной точки (Х,У) в бесконечный квадрат с вершиной в точке (х, у), лежащей левее и ниже ее. Закон распр дискретной двумерной с.в. (Х,У) может быть задан с помощью таблицы:

X/Y	y1	y2	…	ym	…
x1	p11	p12	…	p1m	…
x2	p21	p22	…	p2m	…
…	…	…	…	…	…
xn	pn1	pn2	…	pnm	…
…	…	…	…	…	…

, где .

Для двумерной с.в. (Х, У) дискретного и непрерывного типов, интегральные ф-ции распр соответственно равны: F(x,y)= ; F(x,y)= , где f(x,y) – плотность вер-ти величины (Х,У). Св-ва ф-ции плотности вер-ти: 1.f(x,y)≥0; 2. ; 3.f(x,y)=F”_xy(x,y); 4.P{(X,Y) D}= .