8.7. Практикум. Создание движущихся изображений
Движение на экране создается по принципу мультипликации: на экран с соответствующей задержкой выводят последовательность кадров с небольшими изменениями положения «движущихся» объектов или объектов «фона», если эффект движения достигается изменением фона.
Сам «перемещаемый» объект может быть двумерным (плоским) и трехмерным (пространственным), причем движение может осуществляться по двум типам траектории: лежащей в плоскости экрана или выходящей за нее.
Из аналитической геометрии известны формулы, по которым можно, зная закон движения, определить изменения положения каждой точки изображения движущегося объекта на экране.
Движение плоских объектов. Любое сложное движение плоских объектов на экране складывается из базовых: перемещения, масштабирования и поворота. Формулы пересчета координат изображений для базовых видов движения следующие.
Рис. 8.9. Элементарные изменения изображения: а - перемещение; б- масштабирование; в - поворот
Перемещение (рис. 8.9, а)
x1 = x + dx,
y1 = y + dy,
где x, у - исходные координаты точки; x1, y1 - координаты точки после перемещения; dx, dy - смещения по оси х и у соответственно.
Масштабирование относительно точки С (хc, уc) (рис. 8.9, б):
x1 =(х-xс)Мх + xс,
y1 =(у-yс)Му + yс,
где Mx, My - масштабы по х и у соответственно; хc, уc - координаты точки, относительно которой ведется масштабирование.
Поворот относительно точки С с координатами (хc, уC,) (рис. 8.9, в):
x1 = (х-xс)cosα + (у-yс)sinα + хc,
y1 = (у-yс)cosα - (х-xс)sinα + yс,
где α - угол поворота.
Пример 8.7. Разработать программу, которая демонстрирует на экране движение прямоугольника: прямоугольник улетает от нас к некоторой точке горизонта, одновременно вращаясь вокруг своей оси.
Обобщенный алгоритм последовательного показа кадров данной задачи выглядит следующим образом.
Начало:
Установить точку отсчета координат (условное время).
Рассчитать координаты квадрата.
Цикл-пока не истекло время или не нажата любая клавиша
Установить цвет рисования.
Изобразить квадрат.
Приостановить выполнение программы на время просмотра кадра.
Установить в качестве цвета рисования цвет фона.
Изобразить квадрат цветом фона - стереть.
Изменить точку отсчета (условное время).
Пересчитать координаты квадрата.
все-цикл
Конец.
В а р и а н т 1. Координаты вершин квадрата будем хранить в специальных массивах х, у, а квадрат рисовать линиями, проводя их из одной вершины в другую. Изображение квадрата будет осуществлять специальная процедура Square.
Пересчет координат вершин реализуем через разложение «движения» прямоугольника на элементарные составляющие (рис. 8.10): эффект удаления от зрителя получим, используя масштабирование относительно точки горизонта, эффект вращения - за счет поворота вокруг геометрического центра.
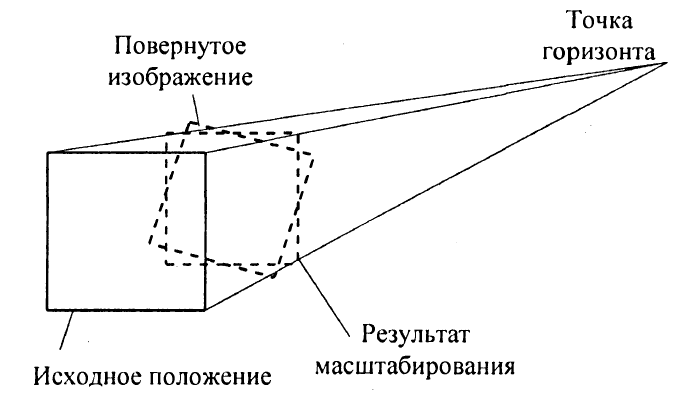
Рис. 8.10. Разложение движения
Вначале определим координаты вершин и центра квадрата после масштабирования, а затем координаты вершин после поворота вокруг центра
квадрата. Ниже приведена соответствующая программа:
Program ex;
Uses Crt,Graph;
Const
r=100;
Type
mas=array[1.. 4] of integer;
Var
x, y, x1, y1:mas;
gd,gm,xn,yn,xc,yc,i,j,k1: integer;
t,k:real;
{изображение квадрата по координатам его вершин}
Procedure Square(х,у:mas);
Begin
Line(x[1],y[1],x[2],y[2]);
Line(x[2],y[2],x[3],y[3]);
Line(x[3],y[3],x[4],y[4]);
Line(x[4],y[4],x[1],y[1]);
End;
{определение координат повернутой точки}
Procedure Pow(xc,yc,x,y:integer;t:real;var xl,yl:integer);
Begin
x1:=xc+round((x-xc)*cos(t))+round(y-yc)*sin(t));
y1:=yc+round((y-yc)*cos(t))-round((x-xc)*sin(t));
End;
{определение координат точки после масштабирования}
Procedure Massch(xc,yc,x,y:integer; k:real; var x1,y1:integer);
Begin
x1:=round(x*k+(1-k)*xc);
y1:=round(y*k+(1-k)*yc);
End;
{основная программа}
Begin
gd:=detect;
InitGraph(gd,gm, 'd:\bp\bgi');
SetColor(2);
xn:=GetMaxX div 4;
yn:=GetMaxY div 3*2;
xc:=GetMaxX-xn;
yc:=GetMaxY-yn;
{расчет начальных координат вершин квадрата}
x[1]:=xn-r; y[1]:=уn-r;
x[2]:=xn+r; у[2]:=yn-r;
x[3]:=xn+r; y[3]:=yn+r;
x[4]:=xn-r; у[4]:=yn+r;
k:=0.99;
t:=0;
{покадровый вывод на экран}
while (t<1) and not KeyPressed do
begin
SetColor(2); {установим цвет рисования}
Square(x,y); {нарисуем квадрат}
t:=t+0.001; {увеличим угол поворота}
{масштабирование}
for j:=1 to 4 do {определим координаты вершин}
Massch(xc,yc,x[j],y[j],k,x1[j],y1[j]);
Massch(xc,yc,xn,yn,k,xn,yn); {определим координаты центра}
{поворот}
for j:=1 to 4 do {определим координаты вершин}
Pow(xn,yn,x1[j],y1[j],-t,x1[j],y1[j]);
for j:=1 to 1500 do Delay(1000); {или NewDelay см. параграф 8.3}
SetColor(0); {установим цвет рисования - цвет фона}
Square(x,y); {стираем квадрат}
x:=x1; {заменим координаты вершин на новые}
y:=y1;
end;
CloseGraph;
End.
Недостатком данного способа является то, что квадрат на экране через несколько кадров уже выглядит не квадратным. Это происходит вследствие накопления ошибки округления при пересчете координат вершин. Избежать этого можно двумя способами:
1) все вычисления выполнять в вещественной арифметике и координаты также хранить как вещественные числа, преобразуя их в целые непосредственно перед использованием в процедуре рисования;
2) пересчитывать координаты не всех вершин, а какой-нибудь одной и центра квадрата, восстанавливая квадрат по одной вершине и положению центра квадрата.
Способы являются взаимодополняющими, поэтому используем оба.
В а р и а н т 2. Для упрощения вычислений вместо массивов, хранящих координаты вершин квадрата, будем использовать смещения этих вершин относительно центра (рис. 8.11). Соответственно процедура рисования квадрата Square 1 должна использовать именно эти параметры. Также учтем, что при масштабировании изменяются размер диагонали и положение центра, а при повороте - смещения вершин относительно центра. Ниже представлен текст программы.
Рис. 8.11. Два соседних кадра при повороте
Program ex;
Uses Crt,Graph;
Const r:real=100; {размер половины стороны квадрата}
Var
x, у, dx, dy, dx1, dy1, xn, yn, xc, yc, xn1, yn1:real;
gd,gm,i,j:integer;
t,k:real; {угол поворота и масштаб}
{изображение квадрата}
Procedure Square1(x,y,dx,dy:integer);
Begin
Line(x+dx,y+dy,x-dy,y+dx);
Line(x-dy,y+dx,x-dx,y-dy);
Line(x-dx,y-dy,x+dy,y-dx);
Line(x+dy,y-dx,x+dx,y+dy);
End;
{основная программа}
Begin
gd:=detect;
InitGraph(gd,gm, 'd:\bp\bgi');
{устанавливаем начальную и конечную точки}
хп:=GetMaxX div 4;
yn:=GetMaxY div 3*2;
xc:=GetMaxX-xn;
yc:=GetMaxY-yn;
{определяем начальные значения}
dx:=r;
dy:=0;
k:=0.95;
t:=0;
{покадровый вывод на экран}
while (t<100) and not Key Pressed do
begin
SetColor(2); {выводим кадр}
Square1(round(xn), round(yn), round(dx), round(dy));
{масштабирование}
xn1:=xn*k+(1-k)*xc;
yn1:=yn*k+(1-k)*yc;
r:=k*r;
{поворот}
t:=t+1; {увеличиваем угол поворота}
dx1:=r*cos(t);
dy1:=r*sin(t);
for j:=1 to 5000 do Delay(1000); {приостановка}
SetColor(0); {стираем кадр}
Square1(round(xn), round(yn), round(dx), round(dy));
dx:=dx1; {заменяем параметры квадрата}
dy: =dy1
xn:=xn1
yn:=yn1
end;
CloseGraph;
end.
Прямая запись в видеобуфер. При программировании на экране движения объектов критичным является время перезаписи изображения: именно из-за большого времени перезаписи движение получается прерывистым.
Для уменьшения этого времени при программировании в MS DOS часто используют прямую запись информации в видеобуфер.
Как указывалось в параграфе 8.4, формат информации в видеобуфере зависит от используемого графического режима. При использовании младших режимов VGA, на которые рассчитан Borland Pascal, видеобуфер содержит 4 бита на каждую точку, причем биты расположены в параллельных битовых плоскостях и доступ к ним напрямую существенно затруднен (программирование таких операций обычно выполняется на ассемблере). Однако существует режим VGA (режим 19: 200*320 точек 256 цветов из палитры 262144 цвета), при котором каждой точке соответствует байт (8 бит) в видеобуфере.
Именно этот режим и используется, если возникает необходимость программировать сложное движение с использованием прямой записи в видеобуфер.
Пример 8.8. Разработать программу, обеспечивающую вывод «бегущей» строки. Направление движения строки по экрану - вверх-вниз.
Для создания изображения используем возможности модуля Graph, затем перепишем изображение из видеопамяти в буфер, расположенный в динамической памяти, и перейдя в режим 200*320, организуем циклический вывод изображения напрямую в видеобуфер. Стирание старого изображения будем выполнять чистой кромкой образа (образ «не прозрачный»).
Переход в другой, не поддерживаемый Borland Pascal графический режим, будем осуществлять, используя ресурсы модуля Dos, описанные далее.
Program ex;
Uses Graph, Crt, Dos;
Type
ScreenType=array[0..199,0..319] of byte; {массив для хранения образа экрана - формат видеобуфера}
ImageType=array[0..999] of byte; {развертка изображения}
ScrTypePtr=^ScreenType; {указатель на массив образа экрана}
ImageTypePtr=^ImageType; {указатель на развертку изображения}
{процедура установки режима с номером mode}
Procedure SetBIOSMode(mode:byte);
Var r:registers;
Begin
r.AL:=mode; {запись номера режима в регистр AL}
r.АН:=0; {запись номера функции в регистр АН}
intr($10,r); {вызов 0-й функции 10-го прерывания}
End;
{основная программа}
Var
Driver, Mode:integer;
s:string;
i, j, n, m, l, y, dy:integer;
Active_Ptr:ScrTypePtr; {указатель на тип "образ экрана"}
Image:ImageTypePtr; {указатель на развертку изображения}
Begin
{формирование изображения и сохранение его в памяти}
Driver: =Detect; InitGraph(Driver,Mode, ");
s:='ABCDEF';
SetColor(4); SetTextStyle(GothicFont, HorizDir, 3);
OutTextXY(2,2,s);
n:=TextHeight(s)+3;
m:=TextWidth(s)+3;
GetMem(Image,(n+1)*(m+1)); {получение памяти для записи изображения}
l:=0;
for i:=0 to n do
for j:=0 to m do
begin
image^[l]:=Lo(GetPixel(j,i)); {запись изображения в буфер}
l:=l+1;
end;
CloseGraph;
{запись изображения «напрямую» в видеобуфер}
SetBIOSMode($13); {установка 19-го графического режима}
Active_Ptr:=Ptr($A000,0); {стандартный адрес видеобуфера}
у:=0;
dy:=1;
{покадровый вывод изображения}
repeat
{побайтная запись изображения в видеобуфер}
l:=0;
for i:=0 to п do
for j:=0 to т do
begin
Active_Ptr^[y+i+10,j+20]:=image^[l];
l:=l+1;
end;
for i:=1 to 1000 do Delay(3000); {задержка}
Inc(y,dy); {смещение изображения}
if (y>120) or (y<0) then dy:=-dy; {организация колебательного движения}
until KeyPressed;
SetBIOSMode(3); {возврат к стандартному текстовому режиму}
End.