4.3. Проверим полученное двухфакторное ортогонализированное уравнение регрессии второго порядка на адекватность по критерию Фишера (результаты расчета внесены в таблицу 6):
‑ рассчитаем
параметр
в каждом опыте по двухфакторному
ортогонализированному
уравнению
регрессии второго
порядка. Например, для
;
‑ образуем
столбец
и рассчитаем остаточную сумму квадратов
(см. уравнение(41)):
;
‑ рассчитаем дисперсию адекватности и её числа степеней свободы (см. уравнения (39), (40)):
;
,
где В – число
значимых коэффициентов двухфакторного
ортогонализированного
уравнения регрессии второго
порядка. В данной задаче
;
‑ рассчитаем экспериментальное значение критерия Фишера (см. уравнение (42)):
,
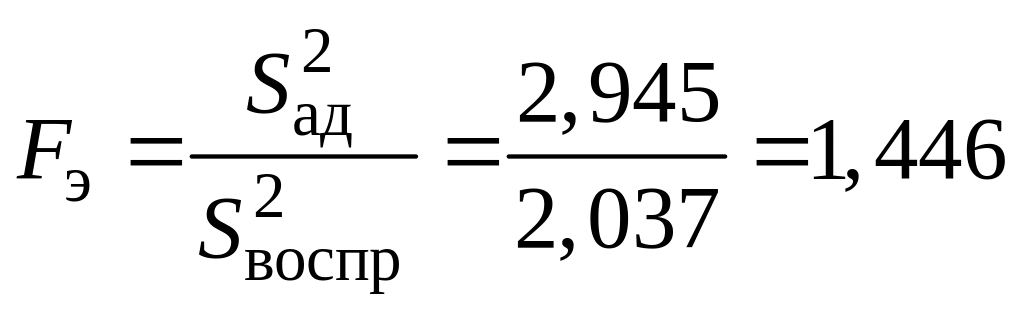так как
;
‑ табличное
значение критерия Фишера
(см. уравнения (43), (44)), в котором на первом
месте стоит число степеней свободы
бльшей
дисперсии, а на втором – число
степеней свободы
мньшей
дисперсии, при доверительной вероятности
выбираем из таблицы приложения 4
.
Вывод. Двухфакторное ортогонализированное уравнение регрессии второго порядка
адекватно,
так как
(см. уравнение (45)).
5. Проведем оптимизацию изучаемой технической системы.
Параметр
Y
имеет
максимум, так как
и
(п. 10).
Найдем
оптимальные значения факторов
,
при которых параметр оптимизации
достигает
,
и рассчитаем абсолютную погрешность
прогнозирования
:
‑ оптимальные
значения нормированных факторов, так
как коэффициент
незначим, рассчитаем по уравнению (53):
;
;
‑ оптимальные значения натуральных факторов рассчитываем по уравнениям (7) – (9) и данным таблицы 4:
;
;
‑ максимальная
урожайность пшеницы
рассчитается по адекватному
двухфакторному
ортогонализированному
уравнению регрессии второго
порядка (см. уравнение (51)), подставляя
в него оптимальные значения значимых
нормированных факторов
;
‑ так как все факторы ортогональны абсолютная погрешность прогнозирования , найденного по адекватному двухфакторному ортогонализированному уравнению регрессии второго порядка
,
рассчитывается по уравнению (52)
.
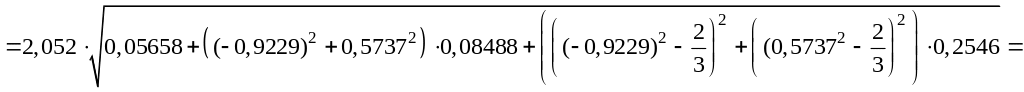
С учётом доверительных
интервалов и алгоритма корректного
оформления результата инженерных и
научных расчётов коэффициенты
запишем в следующем виде:
;
;
;
;
.
Аналогично оформим
результаты расчёта максимальной
урожайности пшеницы
с учетом абсолютной погрешности
.
6. Основной
вывод.
Максимальная урожайность пшеницы
достигается при внесении в почву
семян и
неорганического удобрения.
Ответ.
1) Двухфакторное ортогонализированное уравнение регрессии второго порядка
.
Все 9 выборочных
дисперсий однородны, так как
.
;
;
;
.
Двухфакторное ортогонализированное уравнение регрессии второго порядка адекватно, так как .
2) Результаты
оптимизации:
;
;
;
;
.
Основной вывод.
Максимальная урожайность пшеницы
достигается при внесении в почву
семян и
неорганического удобрения.
Контрольные вопросы
1. Принцип построения МП и ММ для многофакторного ортогонализированного уравнения регрессии второго порядка на базе ОЦКП.
2. Напишите уравнения для расчета коэффициентов двухфакторного ортогонализированного уравнения регрессии второго порядка.
3. Сформулируйте алгоритм проверки коэффициентов двухфакторного ортогонализированного уравнения регрессии второго порядка на значимость по критерию Стьюдента.
4. Сформулируйте алгоритм проверки двухфакторного ортогонализированного уравнения регрессии второго порядка на адекватность по критерию Фишера.
5. Сформулируйте алгоритм определения максимума (минимума) параметра оптимизации.
Контрольные задачи
Таблица 7
Урожайность пшеницы Y приведена в ц/га.
Вар. 1 |
n = 4 |
x1 [1;3] |
x2 [2;3] |
Вар. 2 |
n = 5 |
x1 [2;3] |
x2 [1;4] |
|
Вар. 3 |
n = 6 |
x1 [1;5] |
x2 [2;3] |
|
|
45.5 |
45.8 |
46.6 |
44.1 |
45.5 |
45.8 |
46.6 |
44.1 |
46.0 |
45.5 |
45.8 |
46.6 |
44.1 |
46.0 |
45.1 |
35.9 |
37.1 |
37.1 |
37.9 |
35.9 |
37.1 |
37.1 |
37.9 |
36.8 |
35.9 |
37.1 |
37.1 |
37.9 |
36.8 |
36.0 |
57.4 |
57.9 |
55.6 |
55.2 |
57.4 |
57.9 |
55.6 |
55.2 |
56.8 |
57.4 |
57.9 |
55.6 |
55.2 |
56.8 |
57.2 |
47.9 |
49.0 |
49.7 |
50.2 |
47.9 |
49.0 |
49.7 |
50.2 |
48.9 |
47.9 |
49.0 |
49.7 |
50.2 |
48.9 |
48.4 |
56.7 |
58.7 |
57.7 |
57.4 |
58.7 |
58.7 |
57.7 |
57.4 |
58.0 |
57.7 |
58.7 |
57.7 |
58.4 |
59.0 |
58.9 |
57.4 |
59.1 |
57.1 |
58.2 |
57.4 |
59.1 |
57.1 |
58.2 |
58.4 |
57.4 |
59.1 |
57.1 |
58.2 |
58.4 |
57.2 |
47.7 |
52.9 |
50.6 |
51.4 |
47.7 |
52.9 |
50.6 |
51.4 |
51.3 |
47.7 |
51.9 |
50.6 |
51.4 |
51.3 |
50.8 |
44.5 |
46.6 |
45.4 |
48.0 |
44.5 |
46.6 |
45.4 |
48.0 |
45.7 |
44.5 |
46.6 |
45.4 |
48.0 |
45.7 |
46.2 |
60.7 |
58.5 |
57.8 |
58.8 |
60.7 |
58.5 |
57.8 |
58.8 |
58.5 |
59.7 |
58.5 |
57.8 |
58.8 |
59.5 |
58.0 |
Вар. 4 |
n = 4 |
x1 [1;4] |
x2 [1;2] |
Вар. 5 |
n = 5 |
x1 [2;4] |
x2 [1;4] |
|
Вар. 6 |
n = 6 |
x1 [2;5] |
x2 [2;3] |
|
|
46.5 |
46.6 |
47.6 |
47.6 |
46.5 |
46.6 |
47.6 |
47.6 |
47.1 |
46.5 |
46.6 |
47.6 |
47.6 |
47.1 |
45.6 |
37.4 |
38.0 |
37.4 |
38.1 |
37.4 |
38.0 |
37.4 |
38.1 |
38.4 |
37.4 |
38.0 |
37.4 |
38.1 |
38.4 |
35.0 |
55.6 |
57.5 |
57.5 |
59.7 |
55.6 |
57.5 |
57.5 |
59.7 |
58.4 |
55.6 |
57.5 |
57.5 |
59.7 |
58.4 |
57.0 |
47.6 |
51.1 |
48.6 |
50.2 |
47.6 |
51.1 |
48.6 |
50.2 |
48.5 |
47.6 |
51.1 |
48.6 |
50.2 |
48.5 |
48.5 |
53.5 |
55.6 |
57.4 |
55.0 |
53.5 |
55.6 |
57.4 |
55.0 |
57.0 |
53.5 |
55.6 |
57.4 |
55.0 |
57.0 |
53.9 |
58.1 |
56.2 |
58.9 |
57.5 |
58.1 |
56.2 |
58.9 |
57.5 |
59.6 |
58.1 |
56.2 |
58.9 |
57.5 |
59.6 |
56.8 |
49.1 |
48.1 |
47.7 |
50.5 |
49.1 |
48.1 |
47.7 |
50.5 |
48.0 |
49.1 |
48.1 |
47.7 |
50.5 |
48.0 |
48.3 |
43.7 |
44.1 |
44.4 |
42.0 |
43.7 |
44.1 |
44.4 |
42.0 |
46.6 |
43.7 |
44.1 |
44.4 |
42.0 |
46.6 |
44.2 |
56.6 |
57.3 |
57.3 |
56.6 |
56.6 |
57.3 |
57.3 |
56.6 |
57.7 |
56.6 |
57.3 |
57.3 |
56.6 |
57.7 |
57.9 |
Вар. 7 |
n = 4 |
x1 [1;4] |
x2 [1;4] |
Вар. 8 |
n = 5 |
x1 [2;4] |
x2 [1;2] |
|
Вар. 9 |
n = 6 |
x1 [2;3] |
x2 [1;2] |
|
|
46.4 |
46.0 |
46.8 |
49.3 |
46.4 |
46.0 |
46.8 |
49.3 |
44.6 |
46.4 |
46.0 |
46.8 |
49.3 |
44.6 |
45.7 |
34.2 |
38.4 |
39.5 |
37.2 |
34.2 |
38.4 |
39.5 |
37.2 |
39.2 |
34.2 |
38.4 |
39.5 |
37.2 |
39.2 |
38.1 |
57.7 |
56.6 |
56.8 |
60.0 |
57.7 |
56.6 |
56.8 |
60.0 |
55.9 |
57.7 |
56.6 |
56.8 |
60.0 |
55.9 |
56.9 |
51.4 |
49.7 |
49.5 |
50.5 |
51.4 |
49.7 |
49.5 |
50.5 |
50.9 |
51.4 |
49.7 |
49.5 |
50.5 |
50.9 |
51.6 |
56.1 |
54.0 |
56.1 |
61.1 |
56.1 |
54.0 |
56.1 |
61.1 |
53.5 |
56.1 |
54.0 |
56.1 |
61.1 |
53.5 |
56.0 |
58.6 |
60.0 |
59.7 |
58.7 |
58.6 |
60.0 |
59.7 |
58.7 |
56.6 |
58.6 |
60.0 |
59.7 |
58.7 |
56.6 |
54.6 |
50.4 |
49.3 |
46.6 |
49.3 |
50.4 |
49.3 |
46.6 |
49.3 |
51.0 |
50.4 |
49.3 |
46.6 |
49.3 |
51.0 |
48.7 |
43.6 |
44.4 |
45.8 |
42.7 |
43.6 |
44.4 |
45.8 |
42.7 |
43.6 |
43.6 |
44.4 |
45.8 |
42.7 |
43.6 |
43.1 |
56.4 |
57.4 |
55.9 |
56.9 |
56.4 |
57.4 |
55.9 |
56.9 |
56.0 |
56.4 |
57.4 |
55.9 |
56.9 |
56.0 |
55.7 |
Вар. 10 |
n = 4 |
x1 [1;3] |
x2 [1;2] |
Вар. 11 |
n = 5 |
x1 [1;5] |
x2 [1;2] |
|
Вар. 12 |
n = 6 |
x1 [2;5] |
x2 [1;3] |
|
|
43.5 |
46.8 |
46.7 |
45.8 |
43.5 |
46.8 |
46.7 |
45.8 |
48.4 |
43.5 |
46.8 |
46.7 |
45.8 |
48.4 |
45.9 |
39.1 |
39.2 |
39.4 |
38.6 |
39.1 |
39.2 |
39.4 |
38.6 |
37.2 |
39.1 |
39.2 |
39.4 |
38.6 |
37.2 |
37.6 |
55.5 |
55.5 |
57.5 |
58.0 |
55.5 |
55.5 |
57.5 |
58.0 |
54.8 |
55.5 |
55.5 |
57.5 |
58.0 |
54.8 |
57.5 |
49.6 |
49.9 |
50.3 |
48.2 |
49.6 |
49.9 |
50.3 |
48.2 |
47.4 |
49.6 |
49.9 |
50.3 |
48.2 |
47.4 |
49.3 |
52.9 |
56.2 |
53.0 |
55.0 |
52.9 |
56.2 |
53.0 |
55.0 |
54.3 |
52.9 |
56.2 |
53.0 |
55.0 |
54.3 |
53.3 |
57.5 |
53.4 |
56.3 |
57.0 |
57.5 |
53.4 |
56.3 |
57.0 |
56.3 |
57.5 |
53.4 |
56.3 |
57.0 |
56.3 |
57.1 |
49.3 |
49.7 |
47.0 |
49.3 |
49.3 |
49.7 |
47.0 |
49.3 |
49.0 |
49.3 |
49.7 |
47.0 |
49.3 |
49.0 |
49.6 |
45.0 |
45.9 |
45.0 |
46.1 |
45.0 |
45.9 |
45.0 |
46.1 |
42.8 |
45.0 |
45.9 |
45.0 |
46.1 |
42.8 |
43.4 |
57.4 |
57.1 |
54.1 |
56.3 |
57.4 |
57.1 |
54.1 |
56.3 |
57.7 |
57.4 |
57.1 |
54.1 |
56.3 |
57.7 |
58.2 |
Вар. 13 |
n = 4 |
x1 [1;2] |
x2 [2;3] |
Вар. 14 |
n = 5 |
x1 [1;3] |
x2 [2;3] |
|
Вар. 15 |
n = 6 |
x1 [2;3] |
x2 [2;3] |
|
|
43.5 |
47.3 |
45.9 |
46.5 |
43.5 |
47.3 |
45.9 |
46.5 |
45.5 |
43.5 |
47.3 |
45.9 |
46.5 |
45.5 |
45.5 |
38.1 |
36.9 |
39.6 |
38.2 |
38.1 |
36.9 |
39.6 |
38.2 |
37.5 |
38.1 |
36.9 |
39.6 |
38.2 |
37.5 |
37.4 |
57.6 |
57.5 |
59.1 |
57.1 |
57.6 |
57.5 |
59.1 |
57.1 |
59.3 |
57.6 |
57.5 |
59.1 |
57.1 |
59.3 |
55.9 |
50.3 |
49.8 |
51.1 |
51.2 |
50.3 |
49.8 |
51.1 |
51.2 |
51.1 |
50.3 |
49.8 |
51.1 |
51.2 |
51.1 |
49.0 |
54.4 |
57.2 |
54.7 |
54.0 |
54.4 |
57.2 |
54.7 |
54.0 |
55.6 |
54.4 |
57.2 |
54.7 |
54.0 |
55.6 |
56.4 |
54.8 |
57.9 |
59.0 |
57.6 |
54.8 |
57.9 |
59.0 |
57.6 |
58.4 |
54.8 |
57.9 |
59.0 |
57.6 |
58.4 |
56.9 |
50.8 |
47.4 |
48.4 |
47.7 |
50.8 |
47.4 |
48.4 |
47.7 |
47.5 |
50.8 |
47.4 |
48.4 |
47.7 |
47.5 |
49.0 |
45.3 |
43.8 |
43.7 |
43.6 |
45.3 |
43.8 |
43.7 |
43.6 |
45.2 |
45.3 |
43.8 |
43.7 |
43.6 |
45.2 |
43.8 |
54.6 |
55.5 |
58.0 |
57.0 |
54.6 |
55.5 |
58.0 |
57.0 |
55.8 |
54.6 |
55.5 |
58.0 |
57.0 |
55.8 |
55.8 |
Продолжение таблицы 7
Вар. 16 |
n = 4 |
x1 [3;4] |
x2 [2;3] |
Вар. 17 |
n = 5 |
x1 [2;5] |
x2 [1;3] |
|
Вар. 18 |
n = 6 |
x1 [2;5] |
x2 [2;3] |
|
|
44.6 |
45.8 |
46.2 |
42.3 |
44.6 |
45.8 |
46.2 |
42.3 |
45.5 |
44.6 |
45.8 |
46.2 |
42.3 |
45.5 |
45.8 |
34.6 |
37.5 |
37.0 |
37.7 |
34.6 |
37.5 |
37.0 |
37.7 |
35.8 |
34.6 |
37.5 |
37.0 |
37.7 |
35.8 |
36.5 |
56.1 |
60.2 |
57.6 |
58.0 |
56.1 |
60.2 |
57.6 |
58.0 |
57.2 |
56.1 |
60.2 |
57.6 |
58.0 |
57.2 |
58.3 |
52.7 |
49.6 |
48.3 |
48.4 |
52.7 |
49.6 |
48.3 |
48.4 |
47.5 |
52.7 |
49.6 |
48.3 |
48.4 |
47.5 |
48.0 |
54.8 |
53.1 |
56.7 |
53.3 |
54.8 |
53.1 |
56.7 |
53.3 |
59.4 |
54.8 |
53.1 |
56.7 |
53.3 |
59.4 |
56.1 |
59.9 |
56.5 |
57.2 |
57.4 |
59.9 |
56.5 |
57.2 |
57.4 |
58.4 |
59.9 |
56.5 |
57.2 |
57.4 |
58.4 |
57.5 |
50.6 |
51.1 |
49.8 |
46.7 |
50.6 |
51.1 |
49.8 |
46.7 |
48.2 |
50.6 |
51.1 |
49.8 |
46.7 |
48.2 |
49.1 |
45.2 |
45.0 |
44.9 |
43.9 |
45.2 |
45.0 |
44.9 |
43.9 |
45.3 |
45.2 |
45.0 |
44.9 |
43.9 |
45.3 |
45.2 |
55.4 |
56.1 |
55.8 |
55.1 |
55.4 |
56.1 |
55.8 |
55.1 |
56.8 |
55.4 |
56.1 |
55.8 |
55.1 |
56.8 |
55.9 |
Вар. 19 |
n = 4 |
x1 [2;3] |
x2 [1;4] |
Вар. 20 |
n = 5 |
x1 [1;3] |
x2 [1;2] |
|
Вар. 21 |
n = 6 |
x1 [1;3] |
x2 [1;4] |
|
|
44.4 |
45.4 |
42.6 |
45.6 |
46.4 |
45.4 |
42.6 |
45.6 |
48.0 |
44.4 |
45.4 |
42.6 |
45.6 |
48.0 |
48.0 |
37.7 |
37.4 |
37.2 |
38.6 |
37.7 |
37.4 |
37.2 |
38.6 |
38.0 |
37.7 |
37.4 |
37.2 |
38.6 |
38.0 |
39.7 |
56.4 |
58.8 |
56.0 |
57.6 |
56.4 |
58.8 |
56.0 |
57.6 |
59.3 |
56.4 |
58.8 |
56.0 |
57.6 |
59.3 |
58.1 |
51.5 |
48.2 |
51.5 |
49.0 |
52.5 |
49.2 |
52.5 |
49.9 |
47.8 |
51.5 |
48.2 |
51.5 |
49.0 |
46.8 |
51.3 |
55.1 |
58.8 |
55.7 |
56.1 |
55.7 |
59.4 |
56.3 |
56.7 |
57.4 |
55.1 |
58.8 |
55.7 |
56.1 |
56.4 |
56.4 |
58.9 |
56.2 |
55.2 |
57.5 |
58.9 |
56.2 |
55.2 |
57.5 |
58.5 |
58.9 |
56.2 |
55.2 |
57.5 |
58.5 |
55.8 |
50.1 |
51.8 |
49.9 |
48.2 |
50.1 |
51.8 |
49.9 |
48.2 |
47.6 |
50.1 |
51.8 |
49.9 |
48.2 |
47.6 |
48.2 |
46.1 |
44.2 |
43.5 |
46.9 |
46.1 |
44.2 |
43.5 |
46.9 |
43.9 |
46.1 |
44.2 |
43.5 |
46.9 |
43.9 |
45.3 |
56.6 |
58.3 |
54.8 |
55.9 |
56.6 |
58.3 |
54.8 |
55.9 |
56.5 |
56.6 |
58.3 |
54.8 |
55.9 |
56.5 |
54.7 |
Вар. 22 |
n = 4 |
x1 [1;3] |
x2 [1;4] |
Вар. 23 |
n = 5 |
x1 [1;4] |
x2 [1;3] |
|
Вар. 24 |
n = 6 |
x1 [2;4] |
x2 [1;3] |
|
|
46.7 |
46.4 |
46.5 |
45.1 |
46.7 |
46.4 |
46.5 |
45.1 |
48.1 |
46.7 |
46.4 |
46.5 |
45.1 |
48.1 |
47.8 |
39.2 |
39.8 |
38.9 |
38.5 |
39.2 |
39.8 |
38.9 |
38.5 |
39.7 |
39.2 |
39.8 |
38.9 |
38.5 |
39.7 |
40.6 |
59.3 |
56.6 |
57.6 |
57.3 |
59.3 |
56.6 |
57.6 |
57.3 |
56.2 |
60.3 |
57.6 |
58.6 |
58.3 |
57.2 |
55.6 |
50.0 |
49.3 |
47.7 |
49.1 |
50.0 |
49.3 |
47.7 |
49.1 |
50.2 |
50.0 |
49.3 |
47.7 |
49.1 |
50.2 |
51.5 |
52.4 |
55.2 |
56.9 |
53.1 |
52.4 |
55.2 |
56.9 |
53.1 |
57.9 |
52.4 |
55.2 |
56.9 |
53.1 |
57.9 |
56.8 |
55.7 |
58.3 |
54.8 |
57.2 |
55.7 |
58.3 |
54.8 |
57.2 |
55.1 |
55.7 |
58.3 |
54.8 |
57.2 |
55.1 |
57.3 |
49.5 |
48.9 |
49.4 |
48.3 |
49.5 |
48.9 |
49.4 |
48.3 |
50.0 |
49.5 |
48.9 |
49.4 |
48.3 |
50.0 |
48.8 |
47.9 |
47.6 |
45.3 |
44.2 |
47.9 |
47.6 |
45.3 |
44.2 |
46.3 |
47.9 |
47.6 |
45.3 |
44.2 |
46.3 |
46.4 |
59.4 |
58.1 |
55.4 |
55.5 |
59.4 |
58.1 |
55.4 |
55.5 |
55.8 |
59.4 |
58.1 |
55.4 |
55.5 |
55.8 |
54.8 |
Вар. 25 |
n = 4 |
x1 [2;5] |
x2 [1;4] |
Вар. 26 |
n = 5 |
x1 [1;4] |
x2 [2;3] |
|
Вар. 27 |
n = 6 |
x1 [2;4] |
x2 [2;3] |
|
|
45.1 |
42.4 |
47.0 |
44.9 |
45.1 |
42.4 |
47.0 |
44.9 |
44.3 |
45.1 |
42.4 |
47.0 |
44.9 |
44.3 |
42.2 |
35.9 |
36.7 |
38.6 |
36.5 |
35.9 |
36.7 |
38.6 |
36.5 |
37.9 |
35.9 |
36.7 |
38.6 |
36.5 |
37.9 |
35.8 |
57.5 |
58.0 |
58.7 |
56.8 |
57.5 |
58.0 |
58.7 |
56.8 |
57.7 |
57.5 |
58.0 |
58.7 |
56.8 |
57.7 |
58.1 |
50.5 |
48.8 |
49.0 |
51.1 |
50.5 |
48.8 |
49.0 |
51.1 |
49.9 |
50.5 |
48.8 |
49.0 |
51.1 |
49.9 |
48.9 |
55.9 |
55.9 |
56.2 |
53.4 |
55.9 |
55.9 |
56.2 |
53.4 |
56.5 |
55.9 |
55.9 |
56.2 |
53.4 |
56.5 |
54.6 |
57.3 |
57.8 |
56.0 |
57.7 |
57.3 |
57.8 |
56.0 |
57.7 |
56.9 |
57.3 |
57.8 |
56.0 |
57.7 |
56.9 |
56.5 |
51.0 |
51.1 |
48.3 |
49.4 |
51.0 |
51.1 |
48.3 |
49.4 |
46.6 |
51.0 |
51.1 |
48.3 |
49.4 |
46.6 |
49.2 |
42.0 |
46.0 |
42.7 |
45.2 |
42.0 |
46.0 |
42.7 |
45.2 |
46.3 |
42.0 |
46.0 |
42.7 |
45.2 |
46.3 |
46.1 |
53.7 |
54.5 |
56.2 |
55.7 |
53.7 |
54.5 |
56.2 |
55.7 |
56.4 |
53.7 |
54.5 |
56.2 |
55.7 |
56.4 |
59.2 |
Вар. 28 |
n = 4 |
x1 [1;3] |
x2 [1;3] |
Вар. 29 |
n = 5 |
x1 [2;3] |
x2 [1;3] |
|
Вар. 30 |
n = 6 |
x1 [2;5] |
x2 [1;2] |
|
|
45.3 |
43.3 |
42.8 |
44.0 |
45.3 |
43.3 |
42.8 |
44.0 |
45.1 |
45.3 |
43.3 |
42.8 |
44.0 |
45.1 |
45.7 |
39.1 |
37.5 |
40.3 |
34.4 |
39.1 |
37.5 |
40.3 |
34.4 |
36.7 |
39.1 |
37.5 |
40.3 |
34.4 |
36.7 |
37.7 |
59.6 |
57.4 |
57.2 |
58.5 |
59.6 |
57.4 |
57.2 |
58.5 |
57.8 |
59.6 |
57.4 |
57.2 |
58.5 |
57.8 |
57.2 |
49.3 |
49.7 |
50.7 |
49.3 |
49.3 |
49.7 |
50.7 |
49.3 |
50.9 |
49.3 |
49.7 |
50.7 |
49.3 |
50.9 |
48.9 |
56.9 |
57.0 |
57.4 |
59.6 |
56.9 |
57.0 |
57.4 |
59.6 |
57.7 |
56.9 |
57.0 |
57.4 |
59.6 |
57.7 |
56.4 |
57.1 |
56.3 |
59.1 |
59.4 |
57.1 |
56.3 |
59.1 |
59.4 |
57.6 |
57.1 |
56.3 |
59.1 |
59.4 |
57.6 |
56.2 |
50.5 |
50.2 |
49.0 |
49.6 |
50.5 |
50.2 |
49.0 |
49.6 |
48.1 |
50.5 |
50.2 |
49.0 |
49.6 |
48.1 |
50.0 |
41.8 |
45.5 |
45.5 |
44.0 |
41.8 |
45.5 |
45.5 |
44.0 |
45.5 |
41.8 |
45.5 |
45.5 |
44.0 |
45.5 |
44.7 |
57.2 |
56.7 |
58.0 |
54.7 |
57.2 |
56.7 |
58.0 |
54.7 |
55.6 |
57.2 |
56.7 |
58.0 |
54.7 |
55.6 |
54.3 |