3.1. Выполним предварительную обработку экспериментальных данных опытов (результаты расчётов внесены в таблицу 5):

‑ выборочное среднее в каждом опыте (см. уравнение (10))

, .

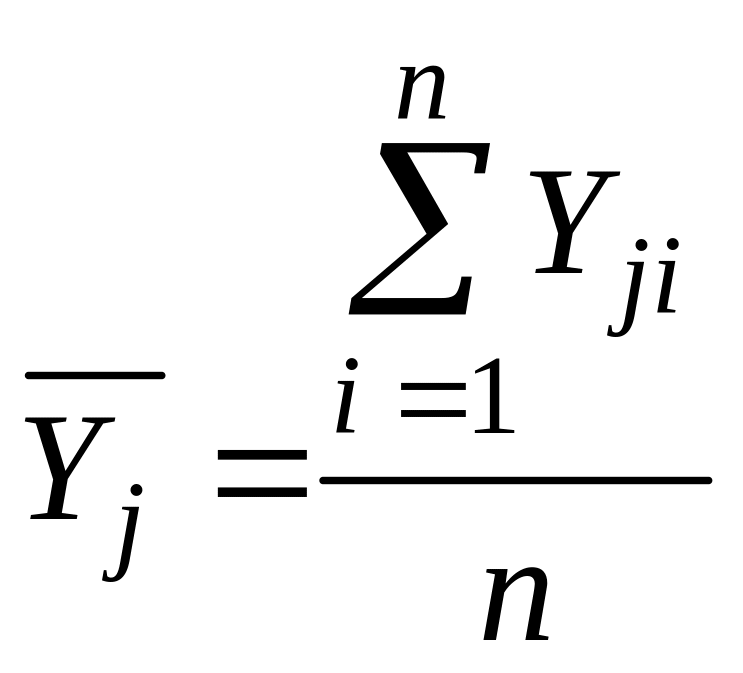Например, выборочное среднее в опыте 8

;

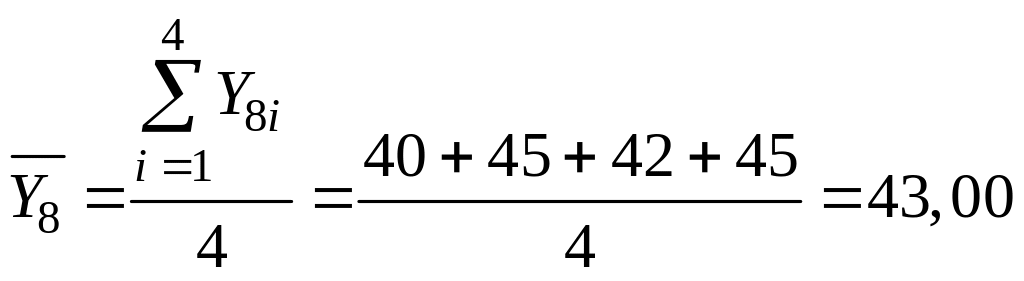‑ выборочная дисперсия в каждом опыте (см. уравнение (11))

, .

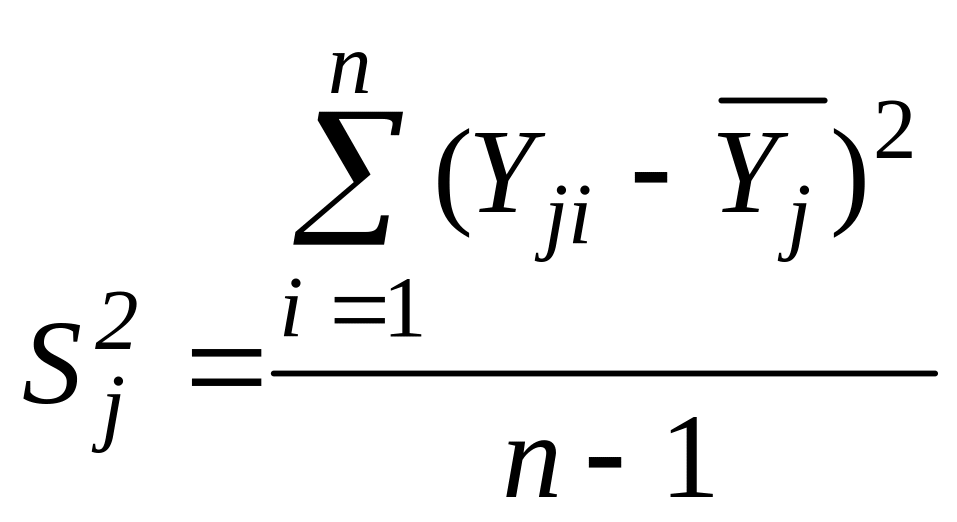Например, выборочная дисперсия в опыте 8

.

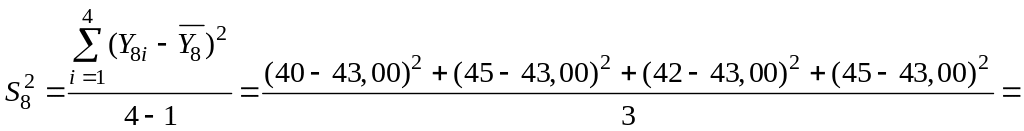
Проверка всех выборочных дисперсий на однородность по критерию Кохрена:

‑ экспериментальное значение критерия Кохрена (см. уравнение (12))

;

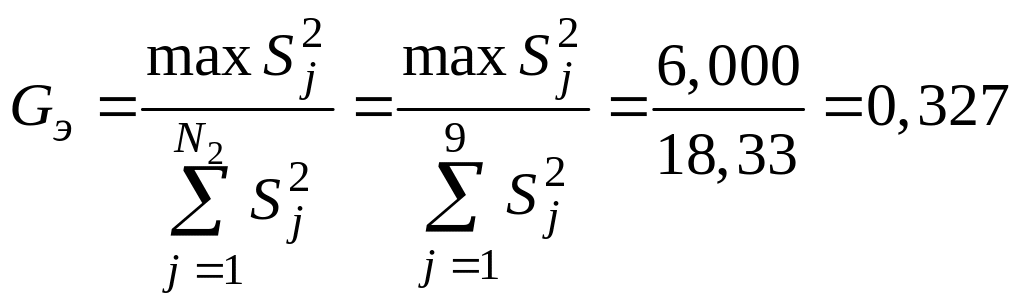‑ табличное значение критерия Кохрена , в котором на первом месте стоит число степеней свободы максимальной дисперсии, а на втором – число степеней свободы , равное числу всех дисперсий, при доверительной вероятности выбирается из таблицы приложения 5.

.

Вывод. Все 9 выборочных дисперсий однородны, так как (см. уравнение (13)).

Так как в каждом опыте число дублей , то проверку случайных значений каждого опыта на промах и на принадлежность их к нормальному закону распределения проводить не будем.

Так как все выборочные дисперсии однородны, рассчитаем дисперсию воспроизводимости и её число степеней свободы по уравнениям (15), (16):

S²_воспр ;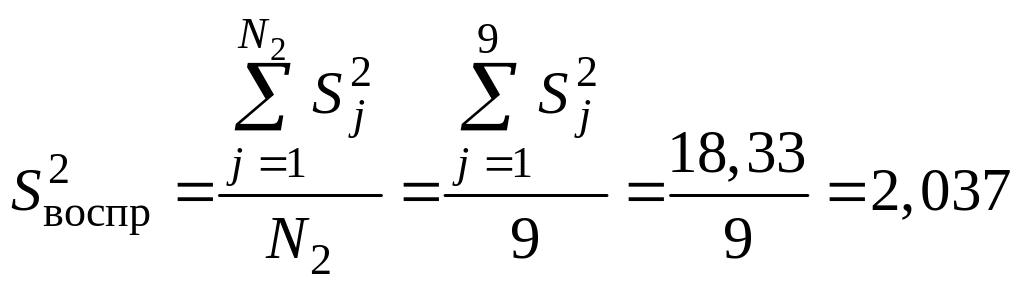

.

4. Создадим ММ на базе ОЦКП для построения ортогонализированного двухфакторного уравнения регрессии второго порядка . (таблица 6). Из уравнения (5) рассчитаем величину ортогонализирующего коэффициента

(сравни с величиной таблицы 1).

В таблице 6 создадим столбцы , .

Таблица 6

ММ для построения ортогонализированного двухфакторного уравнения

регрессии второго порядка на базе ОЦКП с числом опытов .

Результаты окончательной обработки экспериментальных данных

N

1

+

–

–

+

1/3

1/3

45,00

+45,00

– 45,00

– 45,00

+45,00

1/345,00

1/345,00

44,61

0,152

2

+

+

–

–

1/3

1/3

36,00

+36,00

+36,00

– 36,00

– 36,00

1/336,00

1/336,00

36,61

0,372

3

+

–

+

–

1/3

1/3

57,00

+57,00

– 57,00

+57,00

– 57,00

1/357,00

1/357,00

57,61

0,372

4

+

+

+

+

1/3

1/3

49,50

+49,50

+49,50

+49,50

+49,50

1/349,50

1/349,50

49,61

0,012

5

+

0

0

0

– 2/3

– 2/3

54,00

+54,00

054,00

054,00

054,00

– 2/354,00

– 2/354,00

54,94

0,884

6

+

–

0

0

1/3

– 2/3

57,00

+57,00

– 57,00

057,00

057,00

1/357,00

– 2/357,00

56,77

0,053

7

+

+

0

0

1/3

– 2/3

49,50

+49,50

+49,50

049,50

049,50

1/349,50

– 2/349,50

48,77

0,533

8

+

0

–

0

– 2/3

1/3

43,00

+43,00

043,00

– 43,00

043,00

– 2/343,00

1/343,00

42,78

0,048

9

+

0

+

0

– 2/3

1/3

56,50

+56,50

056,50

+56,50

056,50

– 2/356,50

1/3566,50

55,78

0,518

9

6

6

4

2

2

447,5

– 24,00

39,00

1,500

– 4,333

– 11,33

 = 2,945

49,72

– 4,000

6,500

0,3750

– 2,167

– 5,665

Уравнение адекватно

0,49

0,6

0,6

0,7

1,0

1,0

4.1. Рассчитаем коэффициенты ортогонализированного двухфакторного уравнения регрессии второго порядка  . Создадим столбцы , , , , , и рассчитаем суммы (результаты расчётов внесены в таблицу 6):

;

;

;

;

;

Из таблицы 1 найдем значения сумм:

;

;

;

.

Так как все факторы ортогональны коэффициенты двухфакторного ортогонализированного уравнения регрессии второго порядка рассчитывают по уравнениям (17) – (20) (результаты расчётов внесены в таблицу 6):

;

;

;

;

;

.

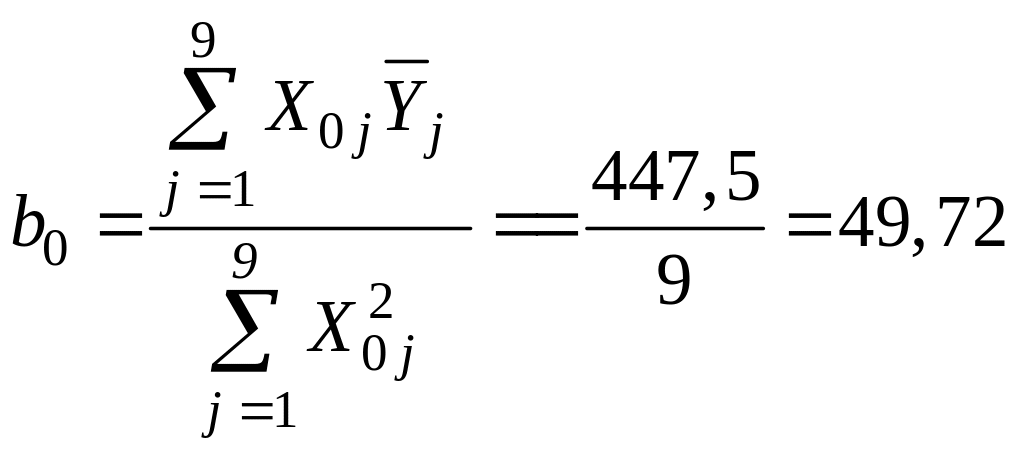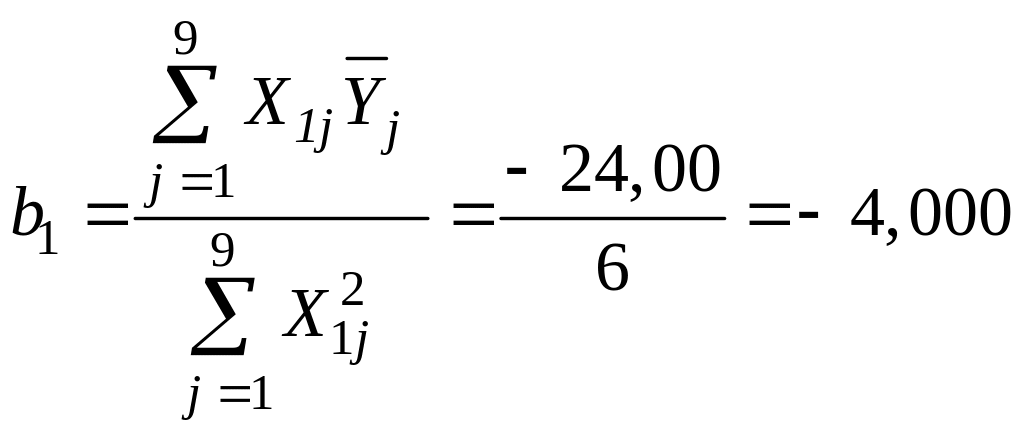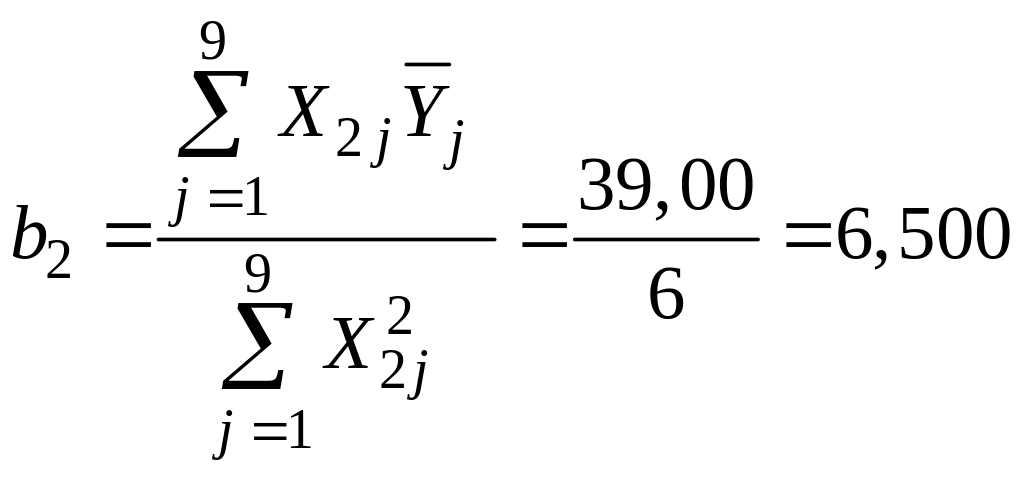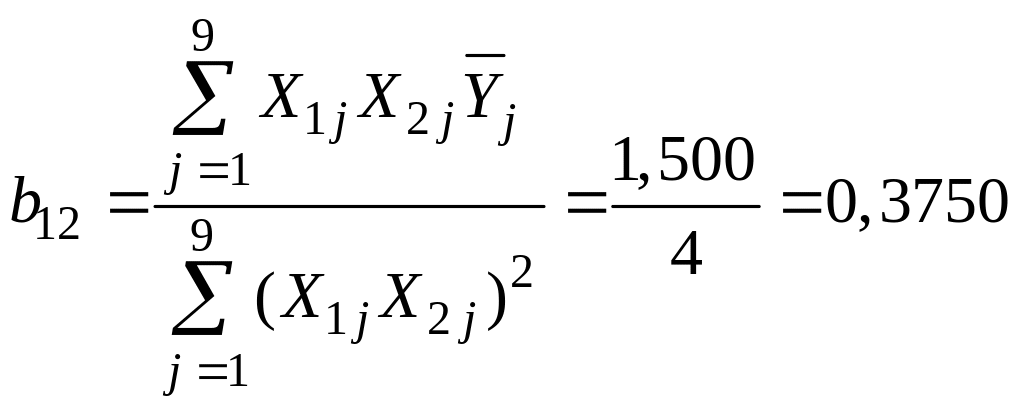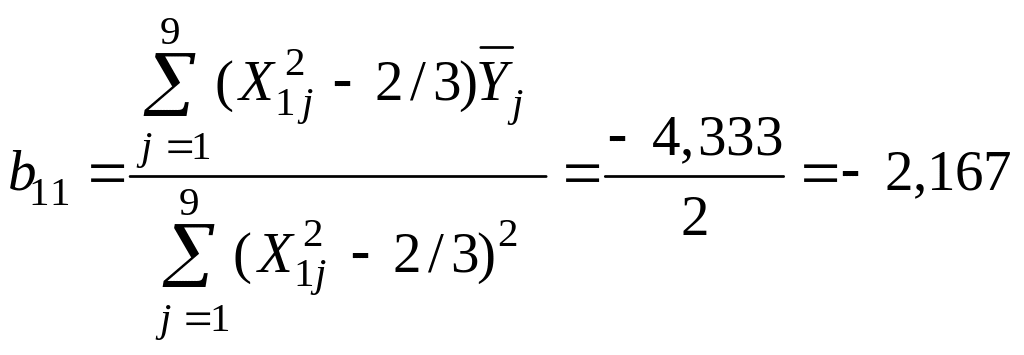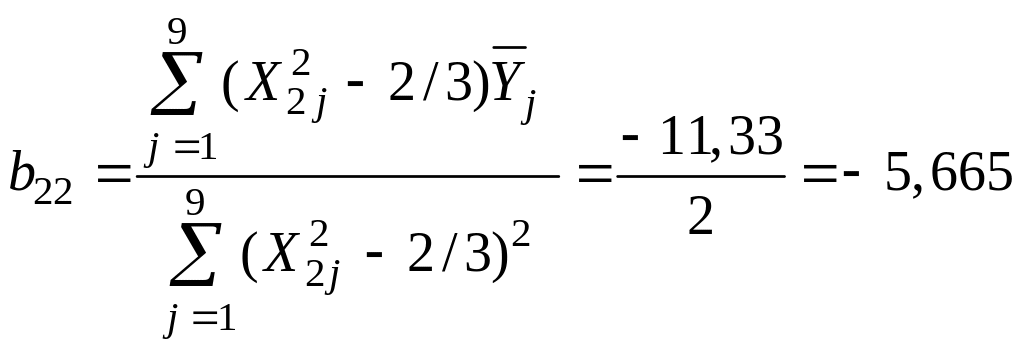4.2. Проверим полученные коэффициенты двухфакторного ортогонализированного уравнения регрессии второго порядка на значимость:

‑ так как все факторы ортогональны дисперсии значимости коэффициентов ортогонализированного двухфакторного уравнения регрессии второго порядка рассчитывают по уравнениям (21) – (24):

;

; ;

; ;

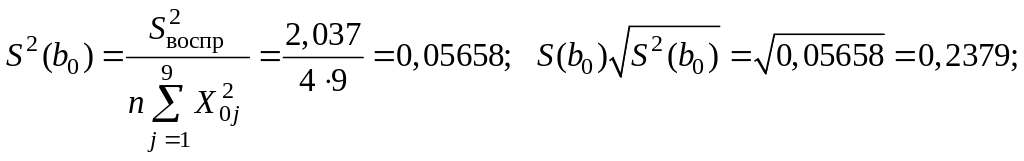
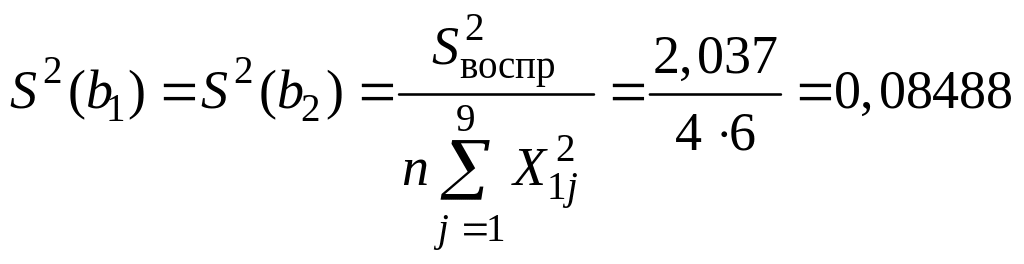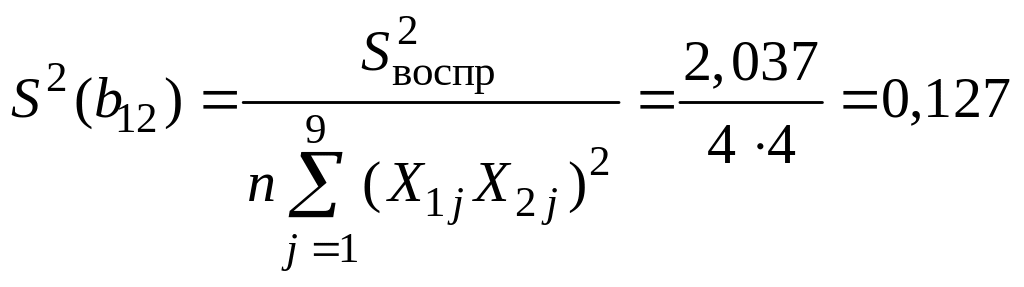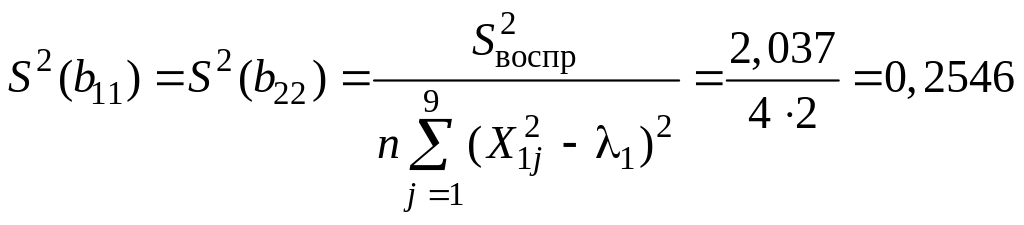‑ рассчитаем доверительные интервалы коэффициентов ортогонализированного двухфакторного уравнения регрессии второго порядка по критерию Стьюдента по уравнениям (28) – (31). Результаты запишем и внесём в таблицу 6 с учётом алгоритма корректного оформления результатов инженерных и научных результатов эксперимента:

;

;

;

,

где  – табличное значение критерия Стьюдента при числе степеней свободы и доверительной вероятности выбираем из таблицы приложения 2.

;

‑ регрессионные коэффициенты значимы, так как (см. уравнения (35), (36)), (38)):

; ,

, , ;

‑ регрессионный коэффициент незначим, так как (см. уравнение (37))

.

Вывод. Двухфакторное ортогонализированное уравнение регрессии второго порядка, в котором коэффициенты значимы, а коэффициент незначим, имеет следующий вид

.