42) Эффект Комптона — называют процесс рассеивания коротковолнового (рентгеновского) излучения на свободных электронах вещества, который сопровождается увеличением длины волны

  

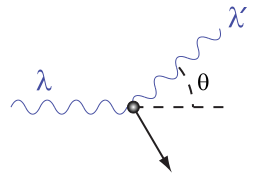
Выводится через Закон сохранения импульса и Закон сохранения энергии

 

 

  

  

  

  

  

  

  

В Формуле мы использовали :

 -Длина волны

 — Угол рассеивания

 - Комптоновская длина волны электрона

 — Скорость света

 — Постоянная Планка

 — Масса электрона

47) Радиоактивность – самопроизвольные превращения атомных ядер, сопровождающиеся испусканием элементарных частиц или более лёгких ядер. Ядра, подверженные таким превращениям, называют радиоактивными, а процесс превращения – радиоактивным распадом.      Радиоактивный распад возможен только тогда, когда он энергетически выгоден, т.е. сопровождается выделением энергии. Условием этого является превышение массы М исходного ядра суммы масс m_i продуктов распада, т.е. неравенство

M >∑m_i.

Э. Резерфорд экспериментально установил (1899), что соли урана испускают лучи трёх типов, которые по-разному отклоняются в магнитном поле:

• лучи первого типа отклоняются так же, как поток положительно заряженных частиц; их назвали α-лучами;

• лучи второго типа обычно отклоняются в магнитном поле так же, как поток отрицательно заряженных частиц, их назвали β-лучами (существуют, однако, позитронныебета-лучи, отклоняющиеся в противоположную сторону);

• лучи третьего типа, которые не отклоняются магнитным полем, назвали γ-излучением.

48) Основная статья: Закон радиоактивного распада

Закон радиоактивного распада — закон, открытый Фредериком Содди и Эрнестом Резерфордом экспериментальным путём и сформулированный в 1903 году. Современная формулировка закона:

что означает, что число распадов за интервал времени t в произвольном веществе пропорционально числу N имеющихся в образце радиоактивныхатомов данного типа.

В этом математическом выражении λ — постоянная распада, которая характеризует вероятность радиоактивного распада за единицу времени и имеет размерность с⁻¹. Знак минус указывает на убыль числа радиоактивных ядер со временем. Закон выражает независимость распада радиоактивных ядер друг от друга и от времени: вероятность распада данного ядра в каждую следующую единицу времени не зависит от времени, прошедшего с начала эксперимента, и от количества ядер, оставшихся в образце.

Этот закон считается основным законом радиоактивности, из него было извлечено несколько важных следствий, среди которых формулировки характеристик распада — среднее время жизни атома и период полураспада^[2][3][4][5].

Константа распада радиоактивного ядра в большинстве случаев практически не зависит от окружающих условий (температуры, давления, химического состава вещества и т. п.). Например, твёрдый тритий T₂ при температуре в несколько кельвинов распадается с той же скоростью, что и газообразный тритий при комнатной температуре или при температуре в тысячи кельвинов; тритий в составе молекулы T₂ распадается с той же скоростью, что и в составе тритированного валина. Слабые изменения константы распада в лабораторных условиях обнаружены лишь для электронного захвата — доступные в лаборатории температуры и давления, а также изменение химического состава способны несколько изменять плотность электронного облака в окружении ядра, что приводит к изменению скорости распада на доли процента. Однако в достаточно жёстких условиях (высокая ионизация атома, высокая плотность электронов, высокий химический потенциал нейтрино, сильные магнитные поля), труднодостижимых в лаборатории, но реализующихся, например, в ядрах звёзд, другие типы распадов тоже могут изменять свою вероятность.

Постоянство константы радиоактивного распада позволяет измерять возраст различных природных и искусственных объектов по распаду входящих в их состав радиоактивных ядер и накоплению продуктов распада. Разработан ряд методов радиоизотопного датирования, позволяющих измерять возраст объектов в диапазоне от единиц до миллиардов лет; среди них наиболее известны радиоуглеродный метод, уран-свинцовый метод, уран-гелиевый метод, калий-аргоновый метод и др.

ПОСТОЯННАЯ РАСПАДА (λ) — статистическая вероятность распада атома за единицу времени; П. р. обратно пропорциональна средней продолжительности жизни (τ) атома изотопа λ=  Связана с периодом полураспада Т_½ соотношением λ=  П. р. — величина постоянная для каждого радиоактивного изотопа и одна из основных его характеристик (константа распада).

Пери́од полураспа́да квантовомеханической системы (частицы, ядра, атома, энергетического уровня и т. д.) — время T_½, в течение которого система распадается с вероятностью 1/2. Если рассматривается ансамбль независимых частиц, то в течение одного периода полураспада количество выживших частиц уменьшится в среднем в 2 раза. Термин применим только к экспоненциально распадающимся системам.

Не следует считать, что за два периода полураспада распадутся все частицы, взятые в начальный момент. Поскольку каждый период полураспада уменьшает число выживших частиц вдвое, за время 2T_½ останется четверть от начального числа частиц, за 3T_½ — одна восьмая и т. д. Вообще, доля выживших частиц (или, точнее, вероятность выживания p для данной частицы) зависит от времени t следующим образом:

.

Период полураспада, среднее время жизни   и константа распада   связаны следующими соотношениями, полученными из закона радиоактивного распада:

.

Поскольку  , период полураспада примерно на 30,7 % короче, чем среднее время жизни.

На практике период полураспада определяют, измеряя активность исследуемого препарата через определенные промежутки времени. Учитывая, что активность препарата пропорциональна количеству атомов распадающегося вещества, и воспользовавшись законом радиоактивного распада, можно вычислить период полураспада данного вещества^[1].