1)

Закон Кулона. Принцип суперпозиции. Электрические поля.

Напряженность электрического поля.

Два заряда взаимодействуют друг с другом так, что сила взаимодействия пропорциональна модулю произведения зарядов и обратно пропорциональна квадрату расстояния между зарядами. Конкретная запись величины силы взаимодействия зависит от системы единиц, которая используется. Так в системе (СГСЕ) (сантиметр, грамм, секунда) заряд является производной величиной, и закон Кулона записывается в виде

,

и это уравнение дает не только величину силы, с которой два заряда взаимодействуют, но и служит для определения размерности заряда 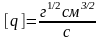— СГСЕ единица заряда. Мы будем пользоваться системой СИ. В этой системе единицей заряда является Кулон (Кл), а закон кулона имеет вид:

.

З десь (в системе СИ) в качестве основной величины выбирается величина заряда, и называется эта величина Кулон (Кл). На самом деле в качестве основной величины в СИ выбирается сила тока равная одному Амперу (А), которая совсем просто связана с единицей заряда 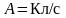. А коэффициенты, входящие в уравнение (2) служат для согласования размерностей и равны

.

.

Величина 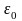называют электрической постоянной (иногда можно встретить устаревшее название диэлектрическая проницаемость вакуума). Важно отметить, что для того, чтобы закон был верен, необходимо выполнение следующих условий:

1. точечность зарядов — то есть расстояние между заряженными телами много больше их размеров.

2. их неподвижность. Иначе уже надо учитывать дополнительные эффекты: возникающее магнитное поле движущегося заряда и соответствующую ему дополнительную силу Лоренца, действующую на другой движущийся заряд.

3. взаимодействие в вакууме.

4. и ещё одно неприятное (особенно для студентов) обстоятельство. В зависимости от системы единиц формулы выглядят по разному (см. (1) и (2)). Поэтому когда будете изучать этот раздел, то пользуйтесь учебником, в котором используется система единиц СИ.

Ну а если у нас нужно найти силу, когда на наш заряд действует не один, а много точечных зарядов? В этом случае сила есть векторная сумма сил, которые действуют на данную частицу со стороны каждой из частиц. При этом сила, с которой i – я частица действует на выделенную частицу считается так, как будто других частиц нет. Такая процедура называется принципом суперпозиции. Все, как и было в механике, берутся все силы, которые действуют на данную частицу со стороны остальных и складываются (Силы это вектора и складываются вектора). Таким образом, если у нас имеется частица с зарядом 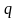и радиус вектором 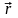и она взаимодействует с N заряженными, неподвижными частицами, то сила, с которой эти частицы действуют на неё согласно принципу суперпозиции равна:

(8)

Получается, что заряженные частицы создают поле, которое и определяет как сильно (и в каком направлении) эти частицы действуют на данный заряд. Это поле можно характеризовать вектором напряженности электрического поля 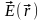, который, согласно (8) равен:

(9)

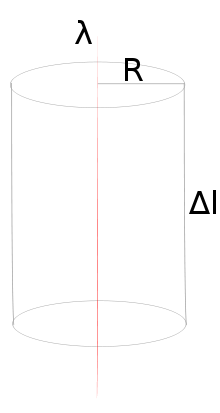
2) Напряженность электрического поля бесконечной нити. Рассмотрим поле, создаваемое бесконечной прямолинейной нитью с линейной плотностью заряда, равной λ. Пусть требуется определить напряжённость, создаваемую этим полем на расстоянии R от нити. Возьмём в качестве гауссовой поверхности цилиндр с осью, совпадающей с нитью, радиусом R и высотой ∆l. Тогда поток напряжённости через эту поверхность по теореме Гаусса таков (в единицахСИ): В силу симметрии

1. вектор напряженности поля направлен перпендикулярно нити, прямо от нее (или прямо к ней).

2. модуль этого вектора в любой точке поверхности цилиндра одинаков.

Тогда поток напряжённости через эту поверхность можно рассчитать следующим образом:

Учитывается только площадь боковой поверхности цилиндра, так как поток через основания цилиндра равен нулю (вследствие направления Eпо касательной к ним). Приравнивая два полученных выражения для  , имеем:

3)Поток вектора через поверхность. Теорема Гаусса.

Для начала посчитаем поток напряженности электрического поля, создаваемого точечным зарядом, через сферическую поверхность с центром в месте расположения заряда. Это помимо прочего покажет нам, что в некоторых случаях интеграл по замкнутой поверхности посчитать не так уж и сложно. Итак:

1. Напряженность электрического поля создаваемая почечным зарядом, который мы поместим в начало координат равна

(18)

2. И нужно вычислить интеграл:

,

(19)

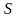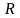где — сфера радиуса с центром в начале координат.

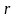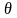Для вычисления интеграла очень важно выбрать форму элементарных площадок, на которые мы разобьем нашу исходную сферу. Т.е. другими словами, какую систему координат мы выберем. Из симметрии нашей задачи, очевидно, что в нашем случае подходит сферическая система координат. Вам известно, что в этой системе координат положение почки задается расстоянием до начала координат , полярным углом и азимутальным углом 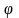. При этом все точки нашей сферы находятся на расстоянии , площадь элементарной поверхности равна 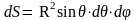. Учитывая, что нормаль к площадке равна 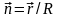, запишем интересующий нас интеграл в виде:

,

(20)

Получился интересный ответ, из которого видно, что интеграл не зависит от радиуса сферы, а зависит только от величины заряда, который внутри этой сферы находится. Больше того, можно доказать (мы этого делать не будем, хотя это и не сложно), что величина интеграла те зависит от формы поверхности. Таким образом, для любой замкнутой поверхности, внутри которой находится заряд , поток вектора напряженности электрического поля не зависит от положения заряда внутри этой поверхности и равен:

,

(21)

Ну а если зарядов внутри поверхности несколько? Ответ очевиден. Согласно принципу суперпозиции напряженность поля от этих зарядов равна сумме напряженности создаваемой каждым зарядом (см. (9)) 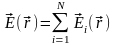и интеграл равен:

,

(19)

Таким образом, мы получили, что интеграл по замкнутой поверхности от напряженности электрического поля равен заряду 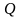, который содержится в внутри поверхности, делённому на электрическую постоянную. Это очень важное уравнение для электростатического поля. Называется это соотношение теоремой Гаусса.

Применение теоремы Гаусса для расчета электрических полей.

4)

(20)

Поле бесконечной заряженной плоскости (см. Рис.3). Поверхностная плотность заряда 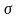(заряд, приходящийся на единицу площади) дана.

Рис.3

Из симметрии задачи следует, что вектор напряженности электрического поля направлен перпендикулярно плоскости и зависит только от расстояния до плоскости. Мысленно выделим цилиндрический объем с площадью основания и высотой 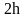, основания на расстоянии 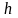в каждую сторону от поверхности. На рисунке показан цилиндр, направления нормалей к основаниям и боковой поверхности и выбранное нами направление вектора напряженности. В таком случае заряд, который попадает внутрь цилиндра, равен 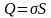, а интеграл по боковой поверхности равен нулю из-за того, что нормаль и вектор напряженности перпендикулярны (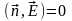 ). В таком случае остаются только интегралы по двум основаниям на которых вектор напряженности постоянен и направлен вдоль нормали. В этом случае теорема Гаусса записывается в виде:

,

(21)

Отсюда получаем:

,

(22)

Таким образом, поле заряженной плоскости не зависит от расстояния до плоскости и направлено от плоскости, если она заряжена положительно 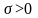и к плоскости, если она заряжена отрицательно 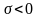. Для дополнительной уверенности в ответе проверим размерность полученного ответа (никогда не помешает), имея ввиду по определению, что

,

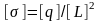
(23)

Сравнивая с (10) делаем вывод, что с точки зрения размерности с ответом все в порядке.

5. Поле бесконечной заряженной нити (см. Рис.4) с линейной плотностью 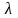Линейная плотность — это заряд единицы длины нити и, значит размерность

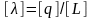
Р ис.4

Для вычисления напряженности поля построим (мысленно) цилиндр радиуса

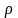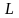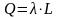и длины по центру которого проходит наша нить. Заряд, попавший внутрь цилиндра равен . Из рисунка видно, что вклад в интеграл дает только боковая поверхность. Поэтому, применяя теорему Гаусса, получаем:

,

что дает:

,
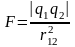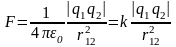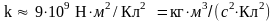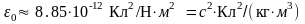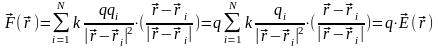
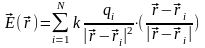
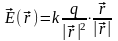
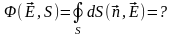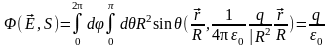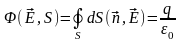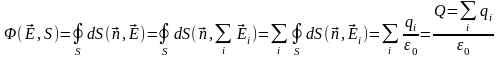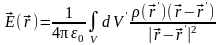
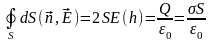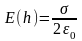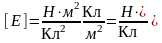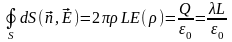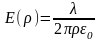