10.Нестационарная теплопроводность при гу 2

Если известна плотность теплового потока q на поверхности тела, то к уравнению Фурье присоединяют ГУ-II в форме

(1.21)

С учетом (1.4) формула (1.21) принимает вид

(1.21)

или

(1.21)

11. Безразмерная форма краевой задачи теплопроводности при гу-III-го рода

Вместо «размерной» температуры T(x,)  [T₀; ] вводится безразмерная относительная температура (x,) по правилу так что в задаче (1.28)–(1.31) надо везде заменить T на , подставив

Далее, вместо размерной протяженности x  [0; l₀] вводится безразмерная протяженность  = x/l₀[0;1], так что в исходной задаче надо везде заменить x на x = l₀.

Задача (1.28) – (1.31) принимает в результате таких подстановок вид (1.28) , (1.29) (1.30)

(1.31) (1.30)

(1.31)

Сформируем безразмерные комплексы в (1.28) и в (1.30). Безразмерный комплекс представляет собой безразмерное время и называется числом Фурье , а безразмерный комплекс представляет собой известную безразмерную интенсивность внешнего теплообмена потока с поверхностью тела и называется критерием Био . Число Фурье Fо содержит в себе аргумент задачи  и поэтому является ее безразмерным аргументом, а критерий Био Bi составлен из известных при постановке задачи параметров.

В конечном виде имеем следующую задачу нестационарной теплопроводности относительно искомой температуры (, Fо)

(1.28)

(1.29) (1.30)

(1.31)

Решение задачи (1.28)–(1.31) отыскивается в виде функции от четырех переменных (вместо девяти в (1.32)) как (1.33)

14. Сеточный метод решения одно- и двумерных задач нестационарной теплопроводности

Метод сеток практически совпадает с методом элементарного теплового баланса. Отличие между ними состоит в том, что, во-первых, метод сеток обосновывается формальной дискретизацией уравнений исходной краевой задачи нестационарной теплопроводности и, во-вторых, полученный таким образом разностный аналог уравнения нестационарной теплопроводности относят ко всем элементарным слоям, на которые мысленно разбивается исходная геометрическая область протекания процесса, т.е. не рассматривают отдельно, как в методе элементарного теплового баланса, пристенные слои Исходное нелинейное уравнение нестационарной теплопроводности, имеющее для неограниченной пластины в одномерной постановке вид , (1.68) при использовании неявной безытерационной схемы дискретизируется относительно середины i-го слоя (рис. 1.11) следующим образом:, (1.69) Приравнивая правые части формул (1.69) , (1.70), получаем разностный аналог уравнения (1.68) в виде

, (1.71)где .Метод сеток позволяет решать и многомерные нелинейные задачи нестационарной теплопроводности. В этом случае на тело наносится сетка, т.е. его, например при рассмотрении двухмерного температурного поля, мысленно делят на элементарные прямоугольники со сторонами и , которые представляют собой шаги по пространственным переменным x и y, при выборе в качестве шага по времени.Можно показать, что в этом случае исходное нелинейное уравнение нестационарной теплопроводности вида (1.78)при использовании безытерационной неявной схемы имеет следующий конечно-разностный аналог:

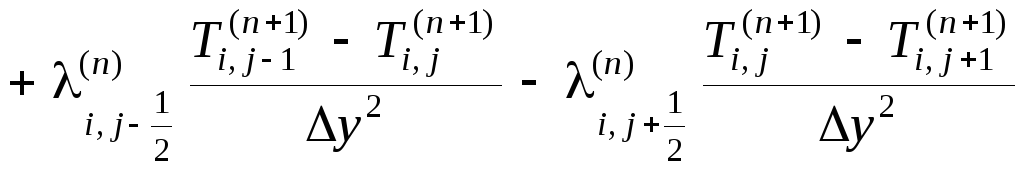, (1.79)

.