41.Третья (основная) теорема теории подобия и моделирования физических явлений

Для подобия двух явлений одинаковой физической природы необходимо подобие распределений, соответствующих условиям однозначности решения исследуемой краевой задачи, т.е. необходимо подобие геометрических областей, свойств среды, начальных и граничных распределений искомых величин, и достаточно равенства одноименных критериев подобия, составленных для сравниваемых явлений.

Ее сформулировали отечественные ученые акад. М.В. Кирпичев и проф. А.А. Гухман, и она названа в их честь теоремой Кирпичева–Гухмана.

42.47.Вывод аргумента Ra для описания теплоотдачи при свободной конвекции

следствием подобия температурных распределений в «натуре» и «модели» является равенство составленных для них чисел Нуссельта. Достаточным же условием для этого подобия при вынужденном движении является равенство критериев Рейнольдса и Пекле.

Достаточным условием для подобия температурных полей при термической свободной конвекции является равенство безразмерных комплексов и критериев Пекле.

.

При термической свободной конвекции неизвестна характерная скорость w₀. Чтобы ее исключить, умножим друг на друга аргументы для числа Нуссельта:

Получившийся при этом безразмерный комплекс составлен из величин, заданных при постановке задачи о развитии процесса свободной конвекции. Он называется критерием Рэлея и обозначается Ra в честь выдающегося физика:

Таким образом, для термической свободной конвекции равенство критериев Рэлея приводит к равенству чисел Нуссельта, так что справедлива зависимость

Nu = f(Ra).

43.Вывод критериев подобия из рассмотрения уравнения нестационарного теплопереноса в потоке (уравнения Фурье-Кирхгофа)

Для вынужденного обтекания потоком пластины или при его течении в прямолинейном канале постоянного поперечного сечения влияние градиента давления отсутствует или незначительно и развитие процесса (формирование распределения скорости) определяется отношением силы инерции к силе вязкостного трения .

оператор (grad):

Мера отношения обозначается как

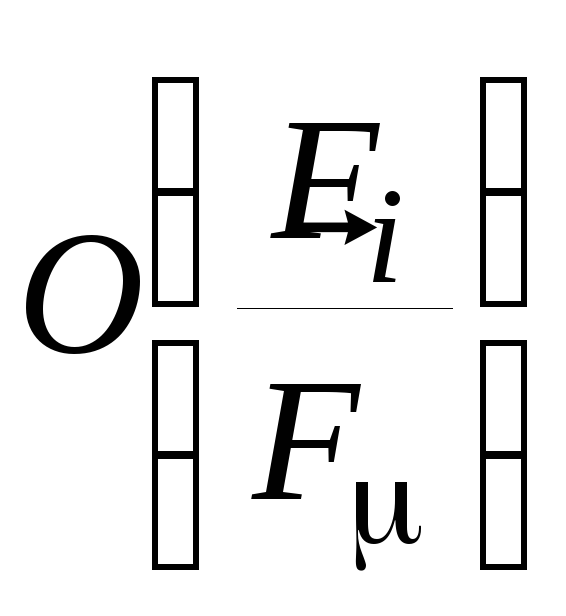
Назначим в качестве меры для известную скорость потока w₀ на входе в трубу, а в качестве меры для протяженностей x, y, z - ее диаметр d.

Безразмерный комплекс в правой части является мерой отношения силы инерции к силе вязкостного трения, его величина определяет характер вынужденного течения жидкости (газа). Он называется критерием Рейнольдса и обозначается Re

или

где  = / - коэффициент кинематической вязкости.

Для подобия распределения скоростей в двух безградиентных вынужденных течениях в каналах достаточно, чтобы выполнялось равенство критериев Рейнольдса, составленных для «натуры» и «модели»:

или

Достаточное условие подобия двух вынужденных течений в более общем виде:

Для подобия температурных полей прежде всего необходимо достаточное условие (при вынужденном движении равенство вычисленных для “натуры” и “модели” критериев Рейнольдса , при термическом свободном движении – равенство безразмерных комплексов , а при гравитационно-вязкостном течении – равенство критерия Рейнольдса и безразмерного комплекса ).

Кроме того, для суждения о подобии температурных полей в двух сравниваемых вынужденных или термических свободных течениях достаточно, чтобы выполнялось равенство

Q_к -сумма количества тепла, вносимого и выносимого движущейся средой механизмом конвекции

Q_т- сумма количества тепла, которое вносится и выносится механизмом молекулярной теплопроводности .

Безразмерный комплекс в правой части является мерой отношения тепловых потоков, переносимых механизмом конвекции и теплопроводности, его величина определяет температурные поля в движущейся среде. Он называется критерием Пекле и обозначается Pe:

Для подобия распределения температуры в двух сравниваемых течениях достаточно, чтобы выполнялись равенства указанных выше безразмерных комплексов, обеспечивающих гидродинамическое подобие течений, и составленных для них критериев Пекле

Pe₁ = Pe₂ или .

Выполняя элементарные преобразования, получаем также

,

где безразмерное отношение называется критерием Прандтля и обозначается Pr